14.02 Задачи №14 из сборника И.В. Ященко
Ошибка.
Попробуйте повторить позже
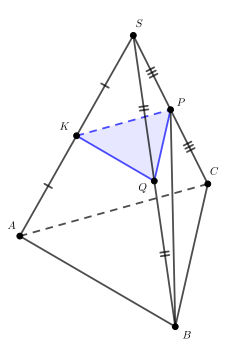
Дана правильная треугольная пирамида сторона основания
высота
точка
— середина
Плоскость, проходящая через точку
и параллельная основанию пирамиды, пересекает ребра
и
в точках
и
соответственно.
а) Докажите, что площадь относится к площади
как
б) Найдите объем пирамиды
Источники:
а) Обозначим плоскость через
По условию плоскости
и
параллельны, следовательно, они пересекают
плоскость
по параллельным прямым. Плоскость
пересекает плоскость
по прямой
плоскость
пересекает плоскость
по прямой
Тогда получаем, что
По аналогичным соображениям
Далее, причем
— середина
следовательно,
— средняя линия в треугольнике
и точка
—
середина
Аналогично получаем, что точка
— середина
Тогда
— средняя линия треугольника
параллельная стороне
Следовательно,
Обозначим через длину высоты треугольника
проведенной из вершины
Так как
— средняя линия, то она
делит эту высоту пополам. Следовательно, высота трапеции
равна
Теперь можем найти отношение площади
к площади
б) Расписав объем пирамиды через объемы ее составных частей, получим
Найдем все эти объемы, чтобы затем найти объем пирамиды
Площадь правильного треугольника со стороной
равна

Высота пирамиды
равна 10, тогда ее объем равен
Далее, найдем следующие отрезки как средние линии соответствующих треугольников:
Следовательно, треугольник подобен треугольнику
по трем сторонам с коэффициентом
Тогда
получаем
Пусть — точка пересечения
с плоскостью
Далее,
следовательно,
— высота пирамиды
Так как
и
— прямые пересечения плоскости
с параллельными плоскостями
и
то они
параллельны. Тогда в треугольнике
отрезок
проходит через середину
и параллелен
Значит,
—
средняя линия и

Тогда можем найти объем пирамиды
Высота из вершины пирамиды
равна
так как
а
и есть расстояние между этими
плоскостями. Тогда можем найти объем пирамиды
Осталось вычислить объем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




