Олимпиада им. Эйлера
Ошибка.
Попробуйте повторить позже
Вершина параллелограмма
лежит на стороне
параллелограмма
Известно, что
и
Докажите, что
Источники:
Подсказка 1
Как можно воспользоваться условием AE=2CD?
Подсказка 2
Давайте отметим точку M - середину отрезка AE (так мы получим, что AM = CD). Что можно сказать про четырехугольник ADCM?
Подсказка 3
Он является равнобокой трапецией. Выведите из этого равенство углов FEM и MDC. Что теперь достаточно доказать про углы MDE и MEB, что завершить доказательство?
Подсказка 4
Достаточно показать их равенство. Как это можно сделать?
Подсказка 5
Можно доказать, что треугольник MDE и BME подобны. Как это можно сделать?
Подсказка 6
Из равенства AC=CD следует равенство углов ACD и CDA. Воспользуйтесь этим, чтобы показать, что углы BMA и AMD равны. Тем самым, мы покажем равенство углов BME и EMD. Осталось проверить равенство отношений соответствующих сторон
Первое решение. Пусть — середина отрезка
Поскольку четырехугольник
— параллелограмм, точка
является
серединой отрезка
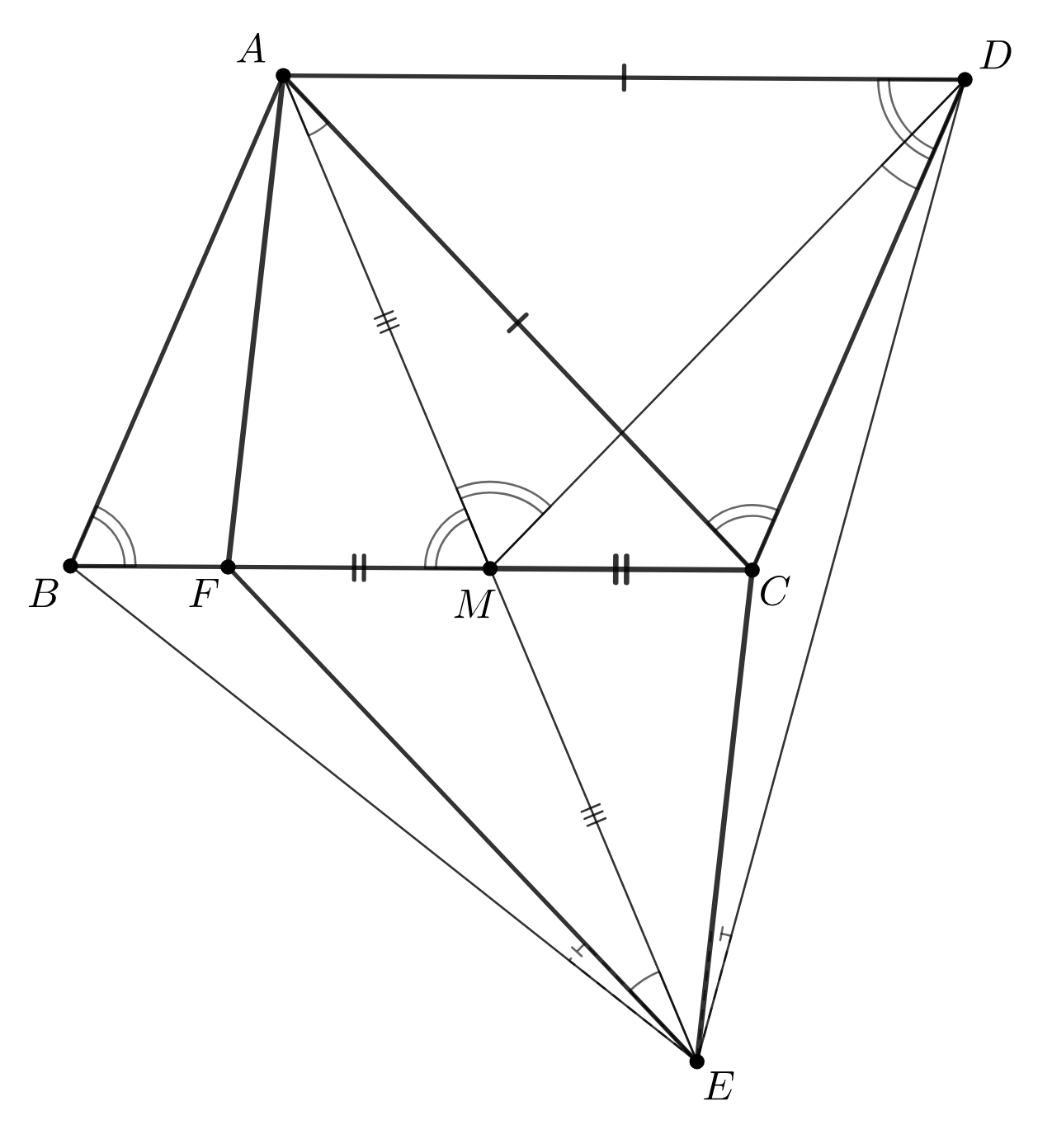
Обозначим и
Так как
— равнобокая трапеция,
откуда мы получаем что
и
Кроме того, поскольку
и
равнобедренные треугольники
и
подобны, поэтому
Треугольники и
также подобны, так как
и Значит,
откуда
что и требовалось.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Как и в первом решении, введём точку и покажем, что
— равнобокая трапеция. Отложим на луче
отрезок
Поскольку
перпендикуляры, опущенные на
из точек
и
равны,
откуда
Поэтому четырёхугольники
и
— также равнобокие трапеции; в частности,
вписана в некоторую окружность
С другой стороны, поскольку отрезки
и
параллельны и равны,
— параллелограмм, откуда
Значит,
— также равнобокая трапеция. Поскольку точки
и
лежат на
точка
лежит на этой же окружности. Из вписанного четырёхугольника
теперь получаем
Осталось заметить, что
— параллелограмм (ибо
параллелен и равен
), откуда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




