Планиметрия на БИБНе
Ошибка.
Попробуйте повторить позже
Дан прямоугольный треугольник 
(
— вершина прямого угла) с острым углом 
при вершине 
Две окружности с центрами
и 
проходят через вершины 
и 
соответственно и касаются прямой 
. Найдите отношение площадей треугольников
и 
, где 
— середина гипотенузы 
.
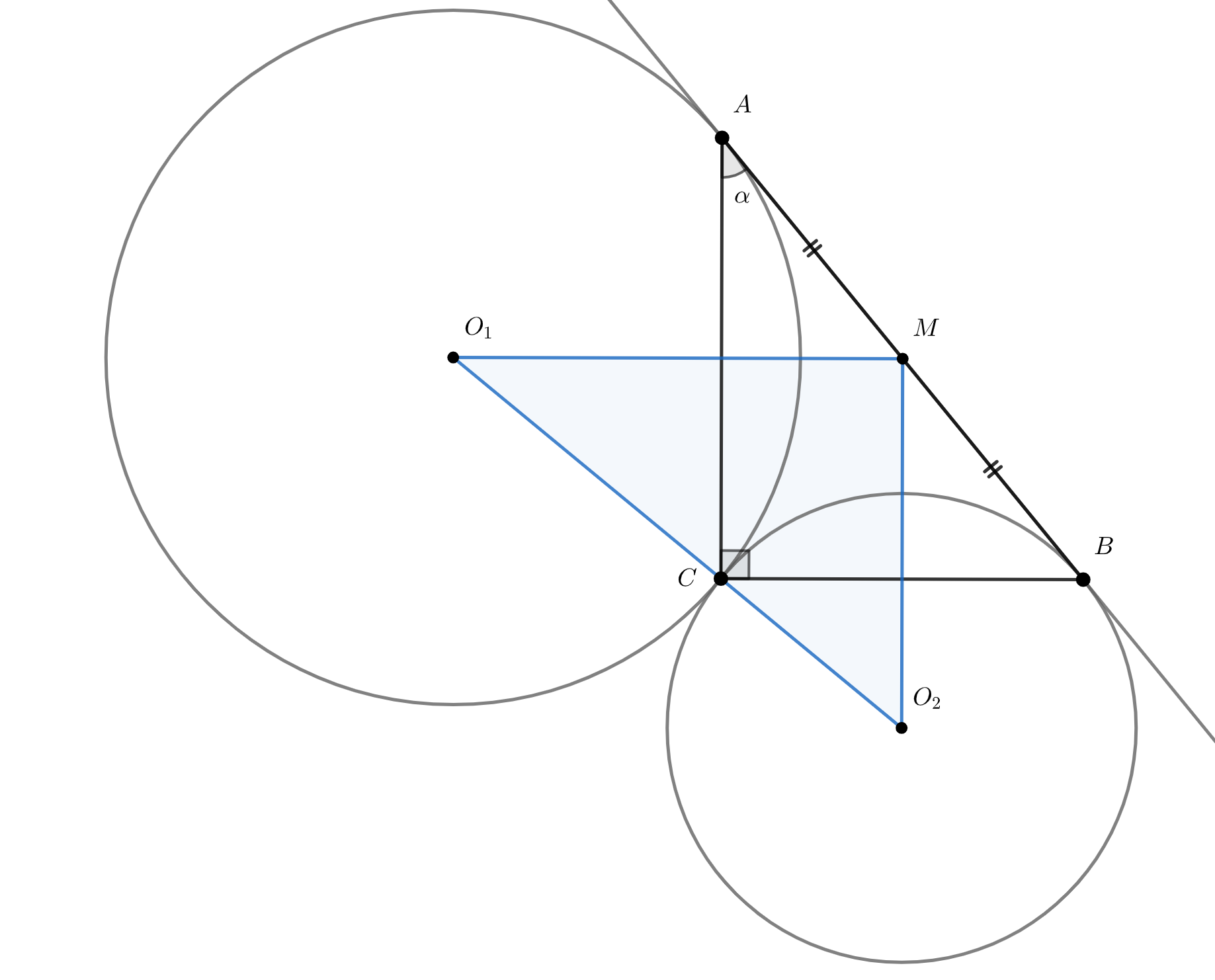
Как центры описанных окружностей, точки 
и 
лежат на серединных перпендикулярах к 
и 
соответственно, причём
пересечением перпендикуляров является точка 
Так как 
и 
взаимноперпендикулярны, то и серединные перпендикуляры
к ним тоже взаимноперпендикулярны. Поэтому треугольник 
— прямоугольный с прямым углом при вершине 
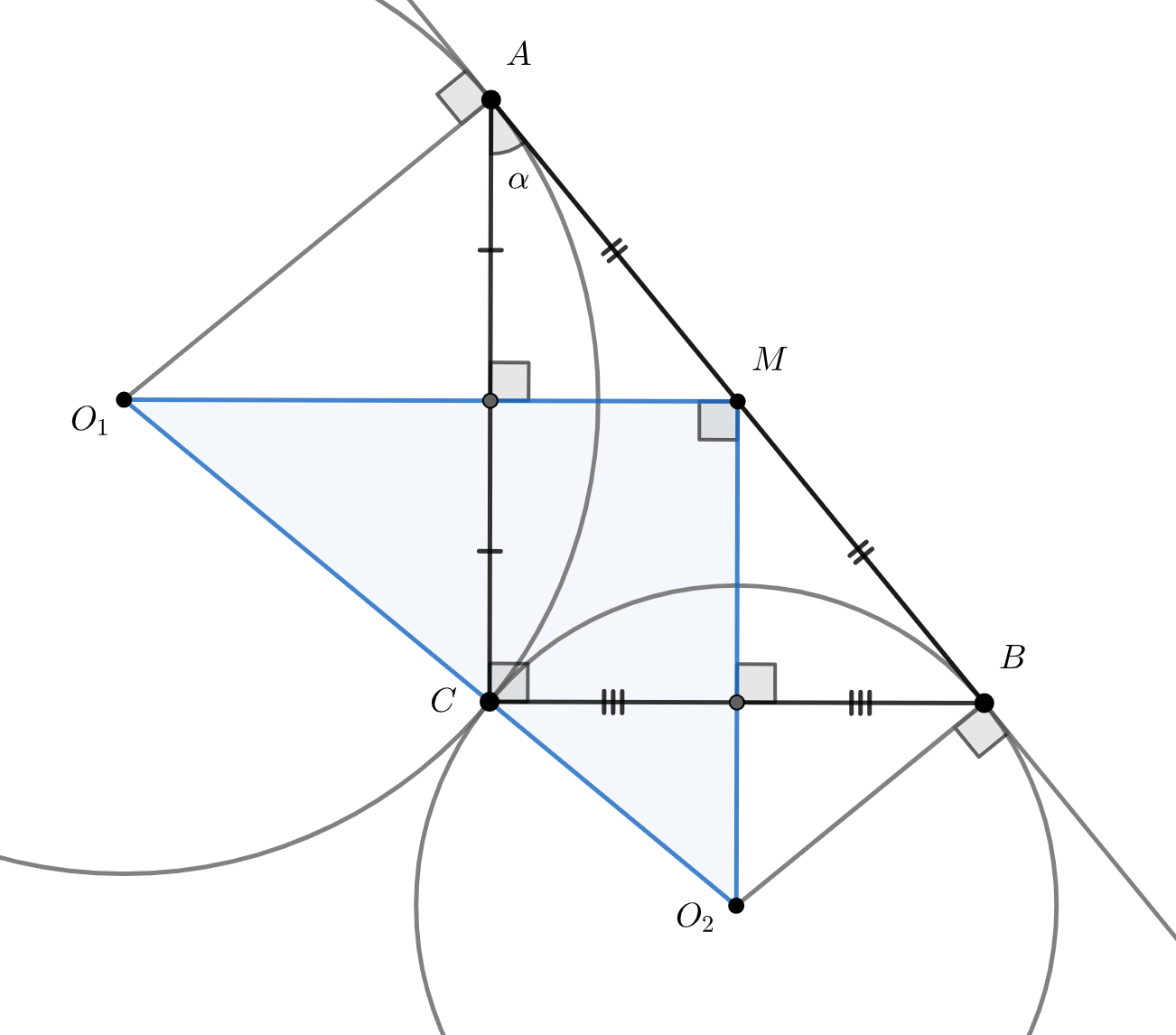
Отношение площадей прямоугольных треугольников равно отношению произведений их катетов, то есть
По условию окружности касаются 
поэтому радиусы 
и 
перпендикулярны касательной 
Тогда из соответствующих
прямоугольных треугольников
В итоге
Так как 
окончательно получаем
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
