Планиметрия на БИБНе
Ошибка.
Попробуйте повторить позже
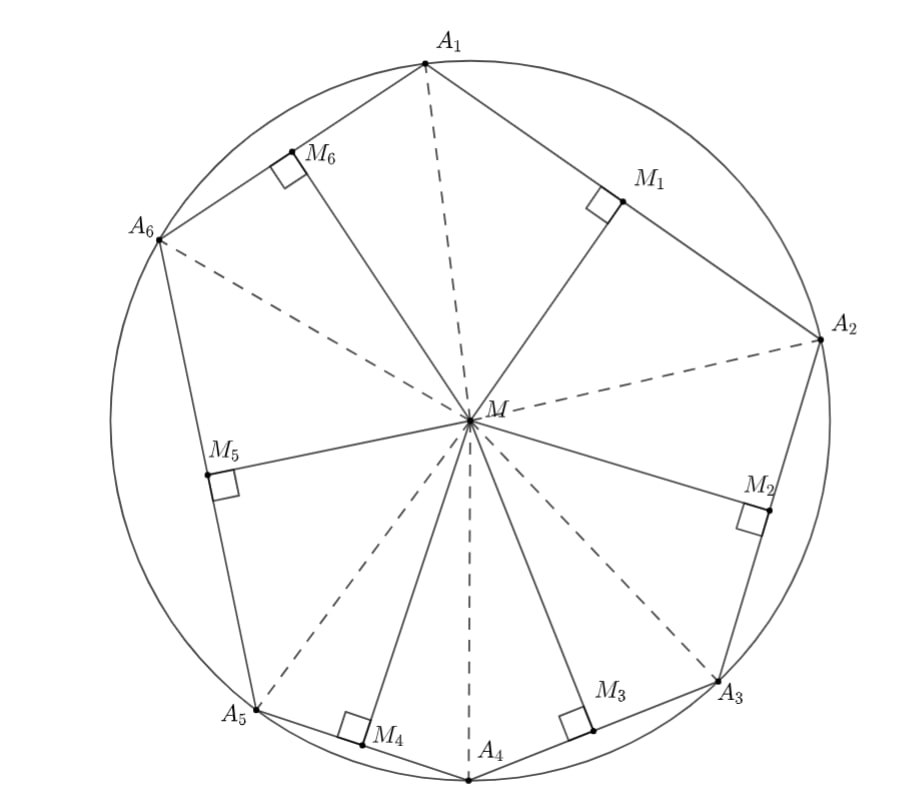
Дан выпуклый 
-угольник 
и точка 
на плоскости. Пусть 
— проекция 
на прямую 
(где 
).
Докажите, что если выполняется равенство
то около 
-угольника можно описать окружность.
Для любого 
от 
до 
по теореме Пифагора 
при этом 
аналогично равно 
Поэтому
При этом
потому что в случае нахождения точки 
вне отрезка 
очевидно даже более сильное 
а в случае
нахождения точки внутри отрезка 
поэтому по неравенству о средних для двух чисел
Итак,
По условию же имеется равенство, так что должно достигаться равенство в каждом из неравенств 
а это
происходит при 
Таким образом, 
является серединой 
для любого 
от 
до 
Поэтому точка 
является точкой
пересечения серединных перпендикуляров к сторонам 
то есть центром описанной окружности. Далее пример для
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
