Проецирование в стерео
Ошибка.
Попробуйте повторить позже
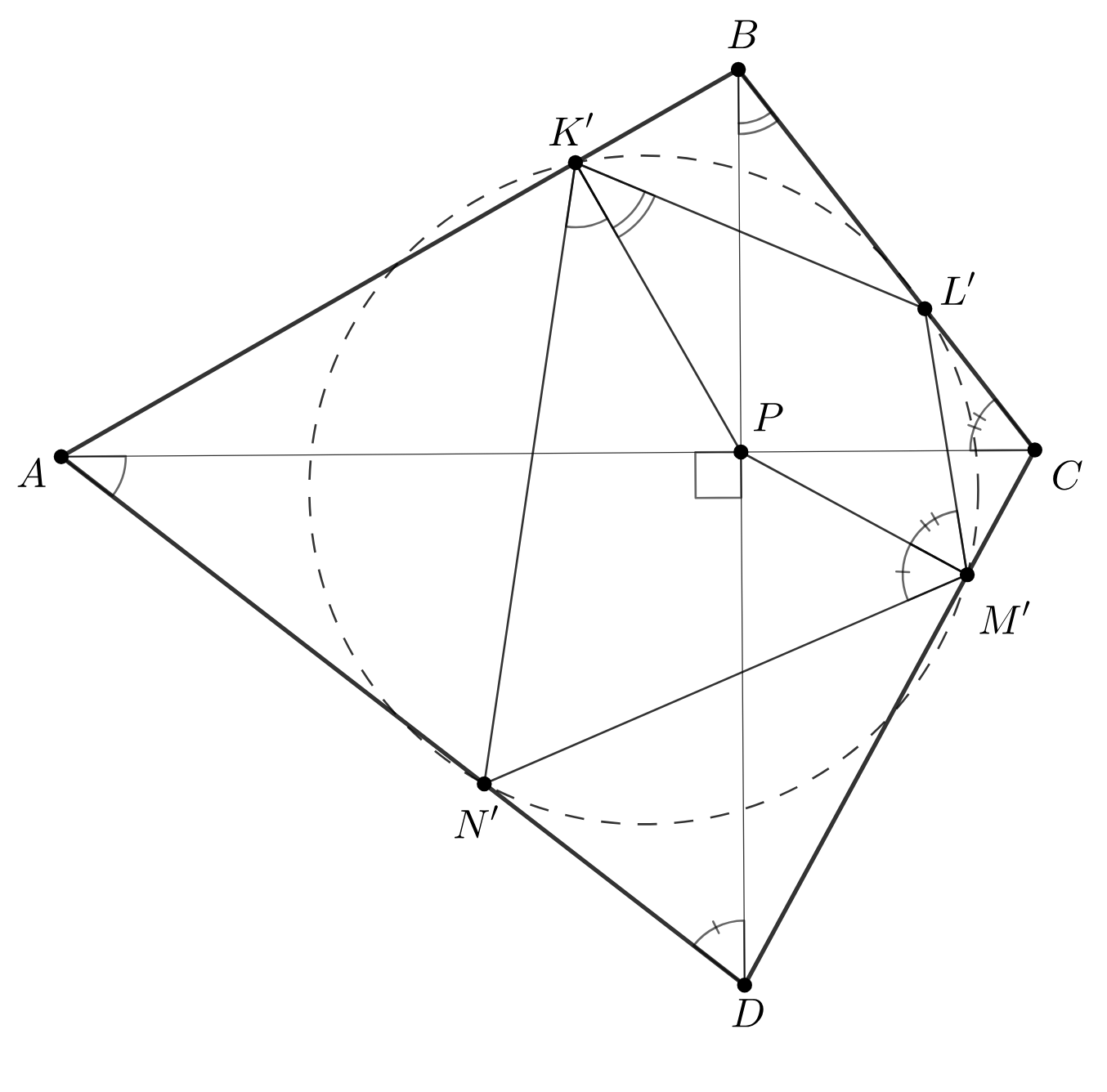
В основании четырехугольной пирамиды 
лежит четырехугольник 
диагонали которого перпендикулярны и пересекаются
в точке 
и 
является высотой пирамиды. Докажите, что проекции точки 
на боковые грани пирамиды лежат на одной
окружности.
Пусть 
и 
— проекции 
на плоскости 
и 
а 
и 
— проекции 
на 
и
Точки 
лежат на одной окружности с диаметром 
следовательно, 
Аналогично,
следовательно,
сумма двух найденных равенств равна сумме противоположных углов четырехугольника 
и равна 
Поскольку 
— высота треугольника 
То есть, треугольники 
и 
подобны и
Из этого и других таких же равенств следует, что
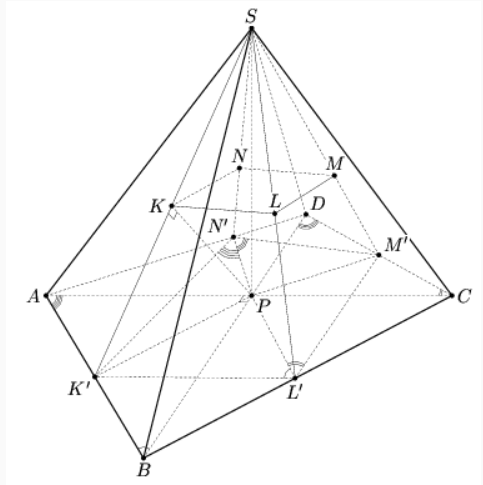
Наконец, для любых четырех точек 
и 
в пространстве выполняется неравенство 
в
котором равенство достигается тогда и только тогда, когда эти точки лежат на одной окружности. Следовательно, точки 
и 
лежат на одной окружности.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
