Тема 1. Геометрия на плоскости (планиметрия)

1.13 Равнобедренная трапеция

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела геометрия на плоскости (планиметрия)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#23885

Сумма двух углов при основании равнобедренной трапеции равна $∘ 50 .$ Найдите больший угол этой трапеции. Ответ дайте в градусах.

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Так как $ABCD$ — равнобокая трапеция, то

∘ ∠ABC + ∠DAB =180 ∠BAD = ∠CDA ∠ABC = ∠BCD

Таким образом, можем считать, что сумма углов $BAD$ и $CDA$ равна $50∘.$ Так как они равны, каждый из них равен $25∘.$

Тогда

∘ ∘ ∘ ∠BCD = ∠ABC = 180 − 25 = 155

Ответ: 155

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#23882

Высота равнобедренной трапеции, проведенная из вершины $C,$ делит основание $AD$ на отрезки длиной 1 и 11. Найдите длину основания $BC.$

$PIC$

Источники: Банк ФИПИ

Показать ответ и решение

$PIC$

Обозначим точки основания высот за $H1,$ $H2.$ Так как трапеция равнобедренная,

AH1 = DH2 = 1

Также $BCH2H1$ — прямоугольник, т.е. $H1H2 = BC.$ Значит,

BC =H1H2 = AH2 − AH1 = 11− 1= 10

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 3#73

Дана трапеция $ABCD$ с основаниями $AD$ и $BC.$ При этом $AB = CD = 6,$ $BC =4,$ а угол $A$ трапеции равен $60∘.$ Найдите длину стороны $AD.$

$PIC$

Показать ответ и решение

Пусть $BE$ — высота трапеции из вершины $B.$ Тогда имеем:

∘ ∘ ∘ ∠ABE = 90 − 60 = 30

Так как в прямоугольном треугольнике катет, лежащий напротив угла $30∘,$ равен половине гипотенузы, то в треугольнике $ABE :$

AE = 0,5⋅6= 3

$PIC$

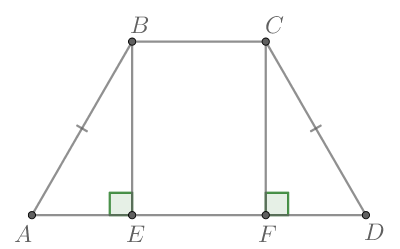
У равнобедренной трапеции углы при одном основании равны, тогда $∠D = 60∘.$

Пусть $CF$ — высота трапеции из вершины $C.$ Тогда $BCF E$ — прямоугольник и $EF = BC = 4.$ Аналогично тому, как находили $AE,$ найдем $FD = 3.$

Тогда искомая длина равна

AD =AE +EF + F D =3 +4 +3 = 10

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 4#74

В трапеции $ABCD :$ $AB = CD,$ $∠C − ∠A =80∘.$ Найдите $∠D + ∠B − ∠C.$ Ответ дайте в градусах.

$PIC$

Показать ответ и решение

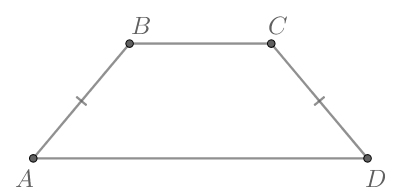
У равнобедренной трапеции углы при одном основании равны, тогда $∠B = ∠C$ и, следовательно,

∠D + ∠B − ∠C =∠D =∠A

У равнобедренной трапеции сумма противоположных углов равна $180∘$ (так как $∠C = ∠B,$ а $∠A + ∠B = 180∘,$ как сумма односторонних при параллельных прямых и секущей).

∘ ∠A + ∠C = 180

∘ ∠C − ∠A =80

Тогда, вычитая из верхнего равенства нижнее, получаем

∘ 2⋅∠A = 100

В итоге имеем:

∠D + ∠B − ∠C =∠A =50∘

Ответ: 50

Ошибка.
Попробуйте повторить позже

Задача 5#539

Диагонали в равнобедренной трапеции $ABCD$ перпендикулярны. Найдите площадь трапеции, если диагональ $AC$ равна $2.$

$PIC$

Показать ответ и решение

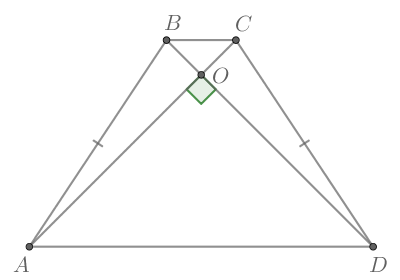
В равнобедренной трапеции диагонали равны, поэтому $AC = BD = 2.$ Пускай $O$ — точка пересечения диагоналей.

1 1 SABCD =S △ABC +S△CDA = 2 ⋅AC ⋅BO + 2 ⋅AC ⋅OD = = 1⋅AC ⋅(BO + OD) = 1⋅AC ⋅BD = 1⋅2⋅2 =2 2 2 2

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 6#540

В равнобедренной трапеции $ABCD$ основание $AD$ вдвое длиннее основания $BC$ и боковой стороны. Найдите площадь трапеции, если боковая сторона равна $√43.$

$PIC$

Показать ответ и решение

$PIC$

Если опустить высоты $BH$ и $CK$ на основание $AD,$ то они отсекут равные отрезки $AH$ и $KD.$ Тогда с учетом условия:

4√- 4√- 14√- AB = BC = HK = 3, AD = 2 3, AH = KD = 2 3

Отсюда по теореме Пифагора для треугольника $ABH$ имеем:

- - 2 2 2 √3-4√3 BH = AB − AH ⇒ BH = 2

Тогда искомая площадь равна

SABCD = 1 ⋅(BC +AD )⋅BH = 9= 2,25 2 4

Ответ: 2,25

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#557

Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна $8.$

$PIC$

Показать ответ и решение

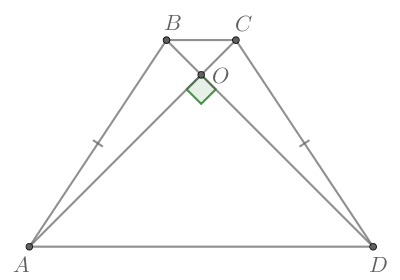
Пусть $ABCD$ — трапеция с диагоналями $AC$ и $BD,$ $O$ – точка их пересечения, тогда

SABCD =S △ABC +S△CDA = 1⋅AC ⋅BO + 1 ⋅AC ⋅OD = 2 2 = 1 ⋅AC ⋅(BO +OD )= 1 ⋅AC ⋅BD = 2 2 = 1 ⋅AC2 =8 ⇒ AC = 4 2

Ответ: 4

Ошибка.
Попробуйте повторить позже

Задача 8#852

Проекция диагонали равнобедренной трапеции на ее большее основание равна $6,$ боковая сторона равна $3.$ Найдите площадь трапеции, если угол при её меньшем основании равен $150∘.$

$PIC$

Показать ответ и решение

$PIC$

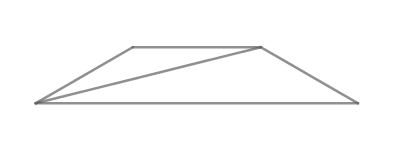
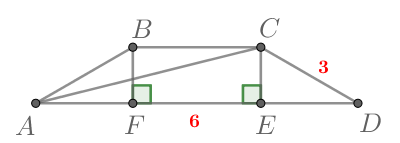
$AE$ — есть проекция диагонали $AC$ на основание трапеции $AD.$ Запишем формулу площади трапеции:

BC + AD S =CE ⋅---2----

Проведя вторую высоту $BF,$ заметим, что треугольники $AF B$ и $DEC$ равны по двум углам и стороне между ними, т. к. боковые стороны в равнобедренной трапеции равны, отсюда следует, что:

AF = ED ⇒ FE = AD − 2ED = BC

Подставим полученные данные в формулу площади трапеции:

CE ⋅ BC-+-AD-= CE ⋅ AD-− 2ED-+AD = 2 2 =CE ⋅ 2⋅(AE-+ED-)−-2ED--=CE ⋅AE 2

Чтобы найти высоту $CE,$ заметим, что

∠ABC = 150∘ ⇒ ∘ ∘ ∘ ⇒ ∠ABF = 150 − 90 = 60 ⇒ ⇒ BF = CE = cos(60∘)⋅AB

Теперь подставим высоту в формулу и найдем площадь трапеции:

S =AE ⋅cos60∘⋅AB = 6⋅ 1 ⋅3= 9 2

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 9#1169

Основания равнобедренной трапеции равны $14$ и $26,$ а ее боковые стороны равны $10.$ Найдите площадь трапеции.

$PIC$

Показать ответ и решение

Проведем высоту $BH.$ По свойству равнобедренной трапеции

AH = (AD − BC ):2= (26− 14) :2= 6

$PIC$

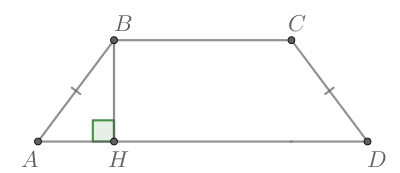
Тогда из прямоугольного треугольника $ABH :$

∘ ---------- ∘------- BH = AB2 − AH2 = 102− 62 = 8

Тогда площадь трапеции:

S = AD-+-BC-⋅BH = 26+-14-⋅8= 160 2 2

Ответ: 160

Ошибка.
Попробуйте повторить позже

Задача 10#1170

Основания равнобедренной трапеции равны $7$ и $13,$ а ее площадь равна $40.$ Найдите боковую сторону трапеции.

$PIC$

Показать ответ и решение

Проведем высоту $BH.$

$PIC$

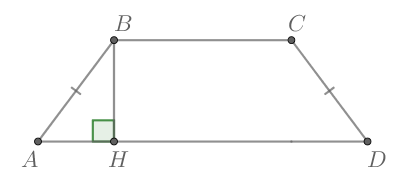
Площадь трапеции равна

AD-+-BC- 7+-13- 40 = 2 ⋅BH = 2 ⋅BH ⇒ BH = 4

Рассмотрим прямоугольный $△ABH.$ По свойству равнобедренной трапеции

AH = (AD − BC ):2 = (13− 7):2 =3

Следовательно,

∘ ---------- AB = AH2 + BH2 = 5

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 11#1171

В равнобедренной трапеции основания равны $12$ и $27,$ острый угол равен $60∘.$ Найдите ее периметр.

$PIC$

Показать ответ и решение

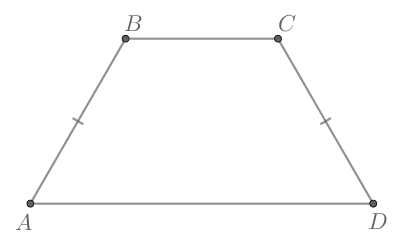
$∠A = 60∘.$ Проведем высоту $BH.$

$PIC$

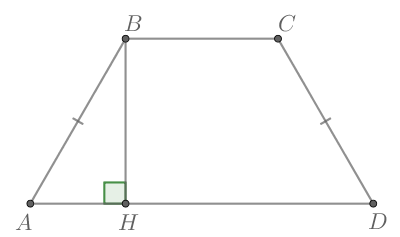
По свойству равнобедренной трапеции

AH =(AD − BC ):2= (27− 12):2= 7,5

В прямоугольном $△ABH :$

∠ABH = 90∘ − 60∘ =30∘

Катет, лежащий против угла $30∘,$ равен половине гипотенузы: $AH =AB :2.$ Значит, $AB = 2AH = 15.$ Следовательно, периметр равен

P = 15+ 15+ 12+ 27= 69

Ответ: 69

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#1172

Основания равнобедренной трапеции равны $15$ и $9,$ один из углов равен $45∘.$ Найдите высоту трапеции.

$PIC$

Показать ответ и решение

$∠A = 45∘.$ Проведем высоту $BH.$

$PIC$

По свойству равнобедренной трапеции

AH = (AD − BC ):2 = (15− 9):2 =3

В прямоугольном $△ABH :$

∠ABH = 90∘ − 45∘ =45∘

Следовательно, $△ABH$ — равнобедренный и

BH =AH = 3

Ответ: 3

Ошибка.
Попробуйте повторить позже

Задача 13#1839

Диагонали в равнобедренной трапеции $ABCD$ перпендикулярны. $O$ — точка пересечения диагоналей, причем $AO :OC = 7:1.$ Найдите периметр трапеции, если меньшее основание равно $1.$

$PIC$

Показать ответ и решение

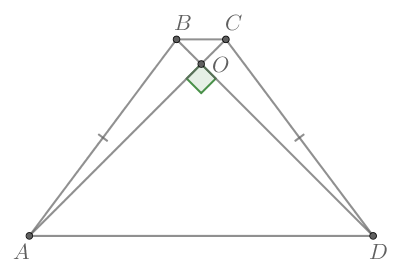
$BC$ — меньшее основание, треугольники $△BOC$ и $△AOD$ подобны и их стороны относятся как $1 :7,$ следовательно, $BC :AD = 1:7.$ Значит, $AD = 7;$ $OB = OC.$ По теореме Пифагора

2 2 2 OB + OC = 1 ⇒ 1-- ⇒ OB =OC = √2 7 ⇒ AO = √2-

В $△ABO :$

AO2 + OB2 = AB2 ⇒ AB = 5

Тогда

PABCD = AB + BC + CD + AD = = 1+ 7+ 5+ 5= 18

Ответ: 18

Ошибка.
Попробуйте повторить позже

Задача 14#1840

В равнобедренной трапеции $ABCD$ биссектриса угла $∠ABC$ параллельна боковой стороне $CD$ и пересекает основание $AD$ в точке $K.$ Сторона $AD$ делится точкой $K$ в отношении $AK :KD = 1:2.$ Найдите периметр трапеции, если меньшее основание равно 4.

$PIC$

Показать ответ и решение

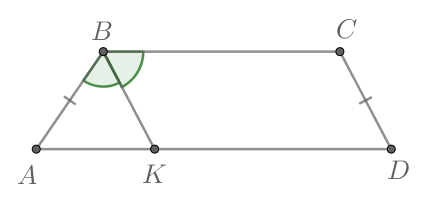
Четырехугольник $BCDK$ — параллелограмм, так как противоположные стороны попарно параллельны. Далее, $∠AKB = ∠KBC$ как накрест лежащие при параллельных $BC$ и $AD$ и секущей $BK.$ Тогда имеем:

∠BAK = ∠CDK = ∠KBC ∠AKB = ∠KBC = ∠ABK

$PIC$

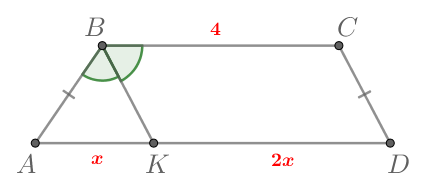
Тогда $△ABK$ — равносторонний. Кроме того,

BC = KD =4 ⇒ AK = 2= AB = CD

Отсюда периметр трапеции равен

PABCD =AB +BC + CD +KD + AK = = 2 +4 +2 +4 +2 = 14

Ответ: 14

Ошибка.
Попробуйте повторить позже

Задача 15#1841

В равнобедренной трапеции $ABCD$ основание $AD$ вдвое длиннее основания $BC$ и вдвое длиннее боковой стороны. Найдите острый угол трапеции.

$PIC$

Показать ответ и решение

Если опустить высоты $BH$ и $CK$ на основание $AD,$ то они отсекут равные отрезки $AH$ и $KD.$ При этом имеем:

AB = BC =HK AD-−-HK-- HK-- AB- AH = 2 = 2 = 2

$PIC$

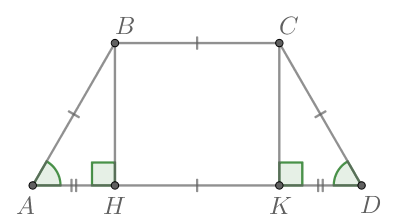
Отсюда $∠ABH = 30∘$ как угол напротив катета, равного половине гипотенузы. Тогда искомый угол равен

∠BAK = 90∘ − 30∘ =60∘

Ответ: 60

Ошибка.
Попробуйте повторить позже

Задача 16#2474

Основания равнобедренной трапеции равны $51$ и $65.$ Боковые стороны равны $25.$ Найдите синус острого угла трапеции.

$PIC$

Показать ответ и решение

Рассмотрим рисунок:

$PIC$

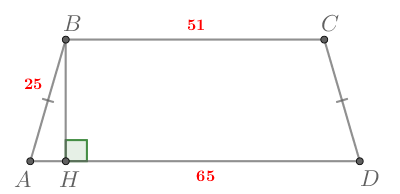
Проведем $BH ⊥ AD.$ По свойству равнобедренной трапеции

1 AH = 2 (AD − BC )= 7

Тогда по теореме Пифагора из $△ABH :$

∘ ------- ∘ ------------- BH = 252− 72 = (25− 7)(25 +7)= √----- = 18 ⋅32 = 3⋅8= 24

Тогда из $△ABH :$

BH 24 sin ∠A = AB--= 25 = 0,96

Ответ: 0,96

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#2523

Основания равнобедренной трапеции равны $14$ и $26,$ а ее периметр равен $60.$ Найдите площадь трапеции.

$PIC$

Показать ответ и решение

Проведем высоту $BH.$ По свойству равнобедренной трапеции

AH = (AD − BC ):2= (26− 14) :2= 6

$PIC$

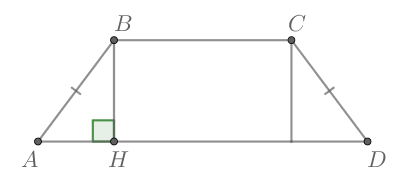
Так как периметр трапеции равен $60,$ а боковые стороны равны, то

AB = 60-− 14-− 26-= 10 2

Тогда из прямоугольного треугольника $ABH :$

BH = ∘AB2--−-AH2-= ∘102−-62 = 8

Тогда площадь трапеции:

AD-+-BC- 26+-14- S = 2 ⋅BH = 2 ⋅8= 160

Ответ: 160

Ошибка.
Попробуйте повторить позже

Задача 18#2524

Основания равнобедренной трапеции равны $7$ и $13,$ а ее площадь равна $40.$ Найдите периметр трапеции.

$PIC$

Показать ответ и решение

Проведем высоту $BH.$

$PIC$

Площадь трапеции равна

AD-+-BC- 7+-13- 40 = 2 ⋅BH = 2 ⋅BH ⇒ BH = 4

Рассмотрим прямоугольный $△ABH.$ По свойству равнобедренной трапеции $AH = (AD − BC ):2 = (13− 7):2 =3.$ Следовательно,

∘ ---------- AB = AH2 + BH2 = 5

Тогда периметр трапеции равен

5 +5 +7 +13 = 30

Ответ: 30

Ошибка.
Попробуйте повторить позже

Задача 19#2525

В равнобедренной трапеции большее основание равно $25,$ боковая сторона равна $10,$ угол между ними $60∘.$ Найдите меньшее основание.

$PIC$

Показать ответ и решение

$∠A = 60∘.$ Проведем высоту $BH.$

$PIC$

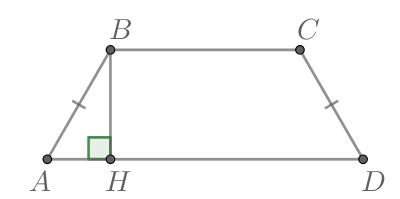
По свойству равнобедренной трапеции $AH = (AD − BC) :2.$ В прямоугольном треугольнике $ABH$

∠ABH = 90∘ − 60∘ =30∘

Катет, лежащий против угла $30∘,$ равен половине гипотенузы:

AH = AB :2= 5

Следовательно,

5 = (25 − BC ):2 ⇒ BC = 15

Ответ: 15

Ошибка.
Попробуйте повторить позже

Задача 20#16090

Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

$PIC$

Показать ответ и решение

Обозначим боковую сторону трапеции через $x.$ Тогда периметр равен

2x+ 14+ 26= 60 ⇔ x= 10

Опустим высоты $BE$ и $CF$ на большее основание $AD.$

$PIC$

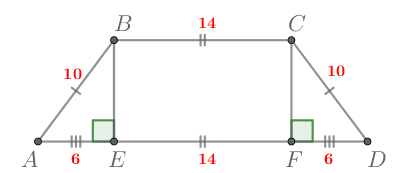
Трапеция равнобокая, $AB = CD,$ $∠EAB =∠CDF,$ следовательно, прямоугольные треугольники $ABE$ и $DCF$ равны и $AE = F D.$ $BCF E$ — прямоугольник, значит, $EF = BC = 14.$ Тогда