Нетабличные углы
Ошибка.
Попробуйте повторить позже
Внутри треугольника 
взята такая точка 
что 
Найдите:
a) углы 
и 
б) расстояние между центрами окружностей, описанных около треугольников 
и 
если 
Источники:
a)
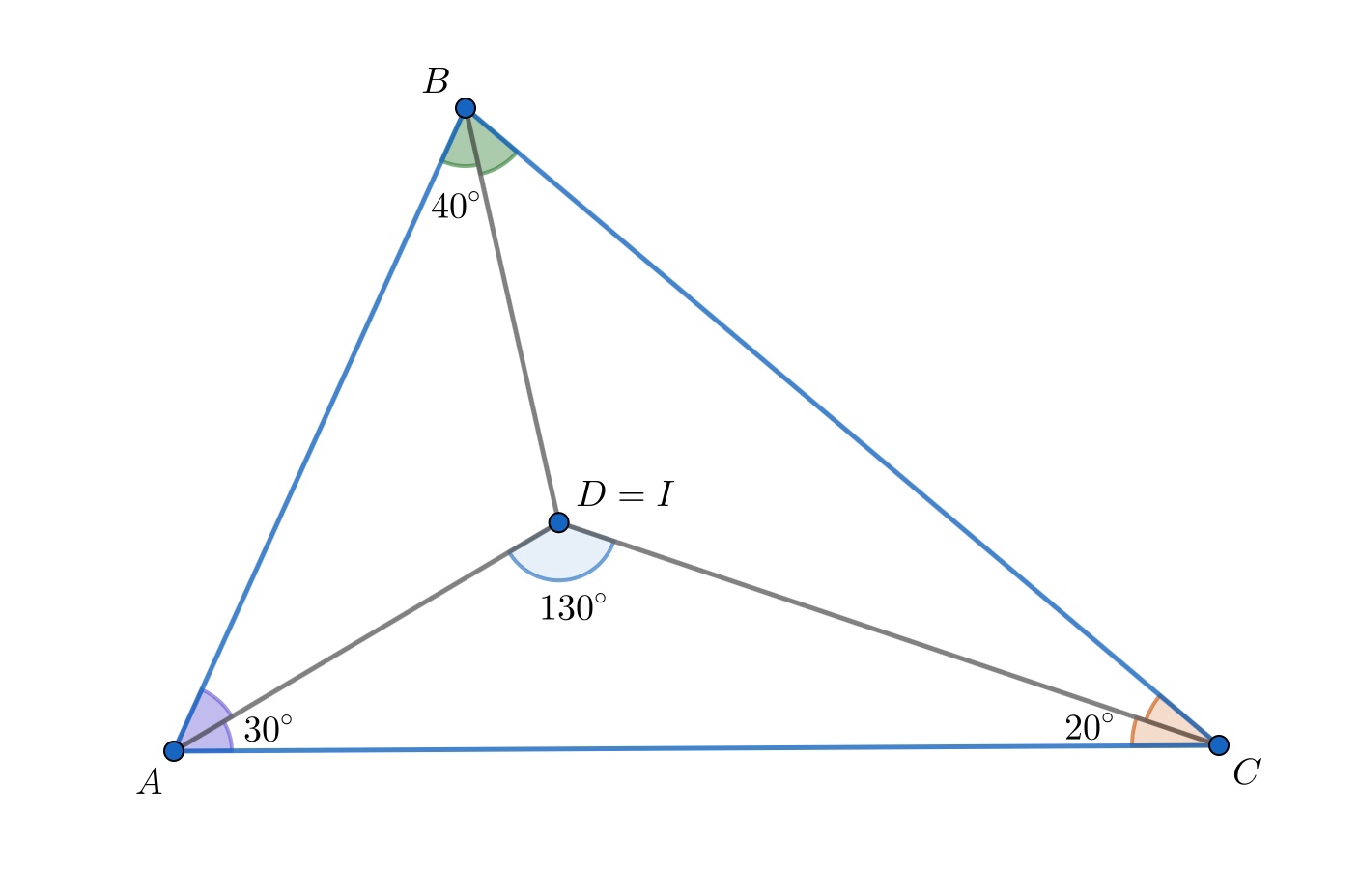
По теореме о сумме углов в треугольнике 
Пусть 
— центр вписанной в треугольник 
окружности. Тогда угол между биссектрисами 
Получается, что из точек 
и 
отрезок 
виден под
одинаковым углом, тогда они лежат на одной окружности вместе с 
. При этом из условия следует, что ещё они обе лежат на одной
прямой (на биссектрисе угла 
), поэтому либо совпадают, либо являются противоположными вершинами прямоугольника (вписанного
параллелограмма) 
. Но так как 
то может быть только случай 
Следовательно, 
и
.
Замечание. Для доказательства 
можно было также воспользоваться условием, что точка 
дана внутри треугольника, и
упростить часть рассуждений.
б)
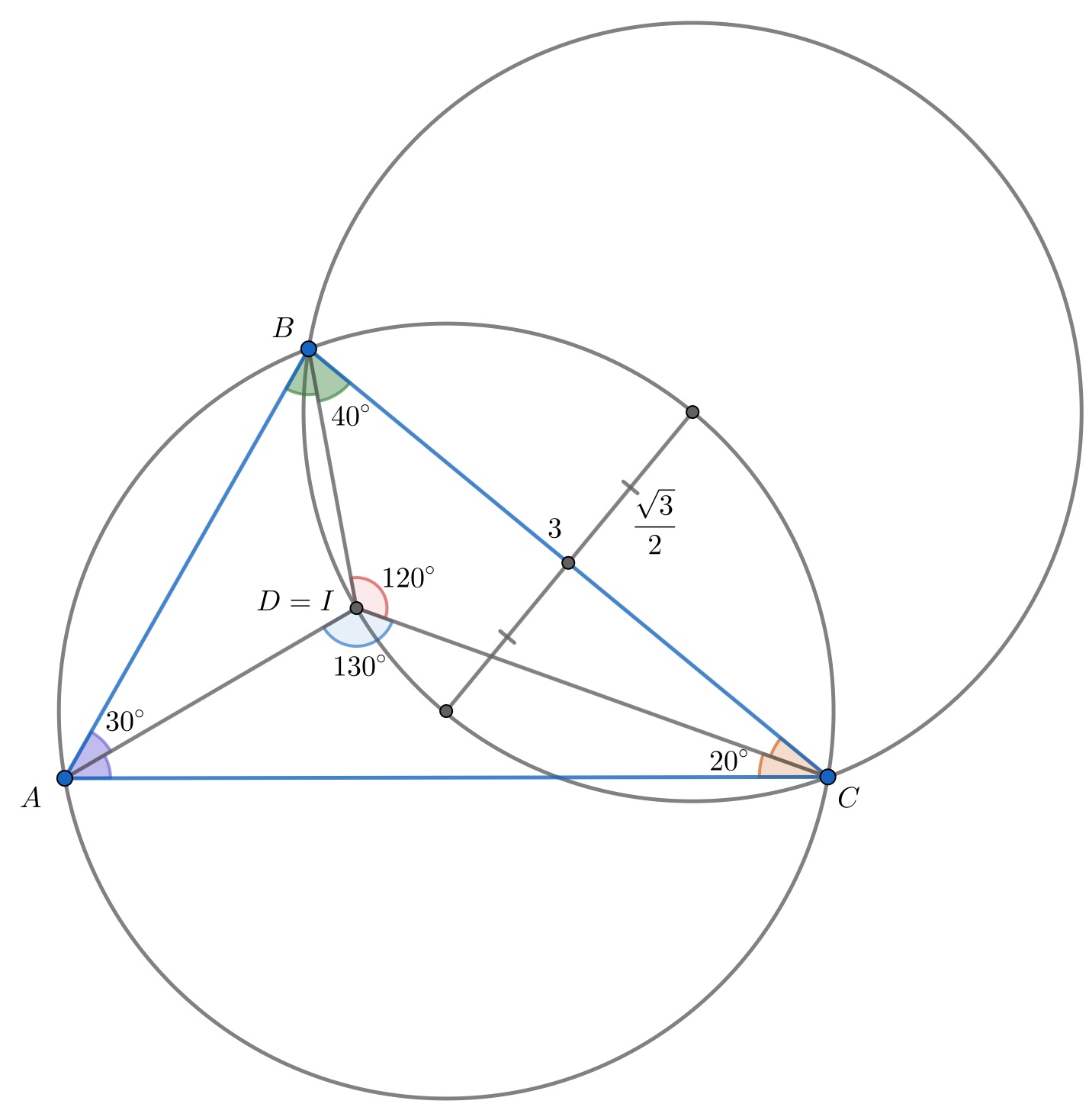
Радиус окружности, описанной вокруг треугольника 
, равен
Но
поэтому радиус окружности, описанной вокруг треугольника 
, также равен
Значит, их общая хорда 
пересекает отрезок между центрами в его середине, а длина этого отрезка равна 
.
а) 
и 
б) 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
