Угадай точку
Ошибка.
Попробуйте повторить позже
Пусть — центр вписанной окружности треугольника
а
и
— центры вневписанных окружностей, касающихся сторон
и
соответственно. Докажите, что точки
и середины отрезков
лежат на одной окружности.
Подсказка 1
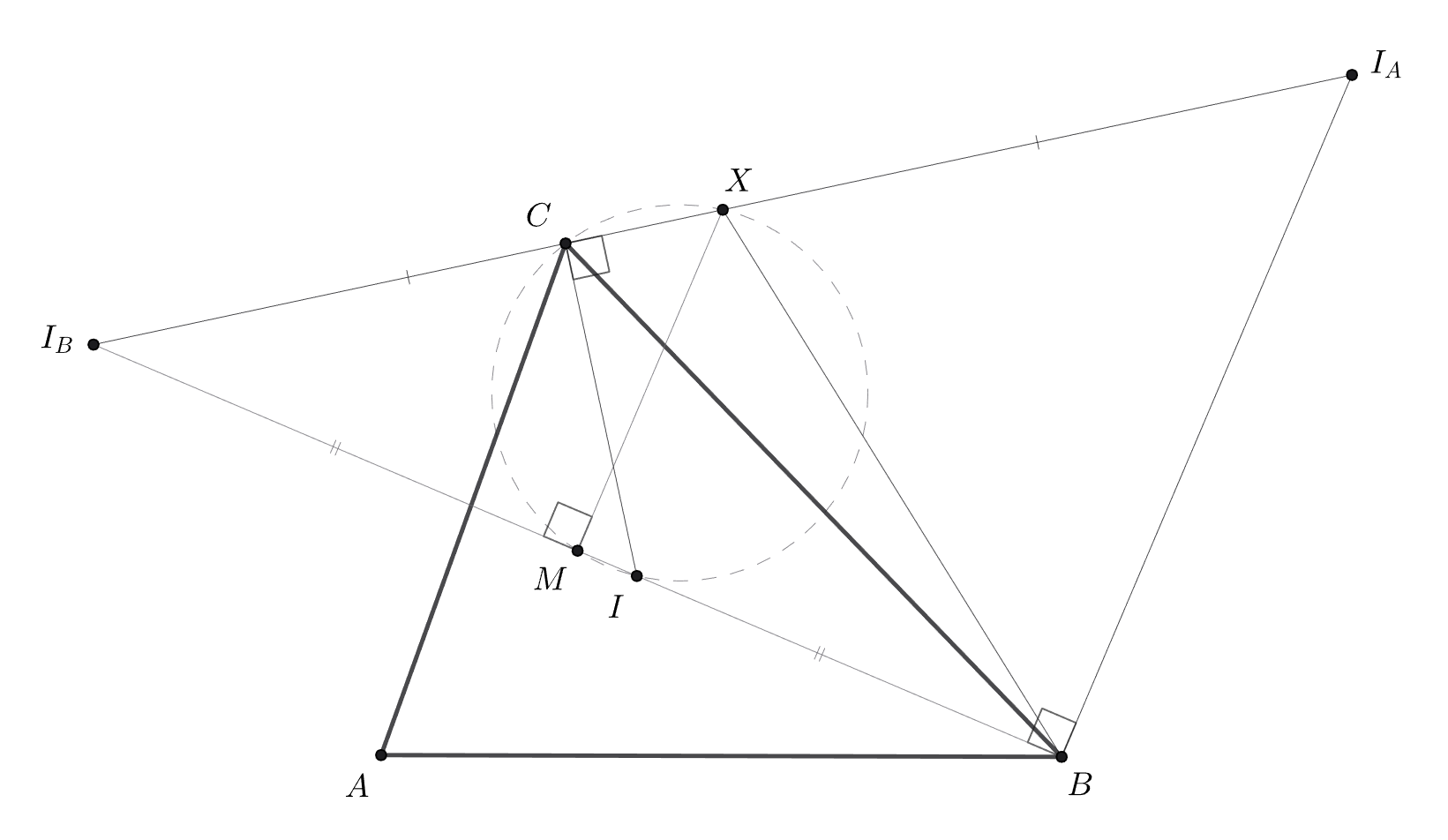
Давайте вспомним факт про 5 точек на окружности. Пусть есть три прямые, пересекающиеся в точке X. Если взять некоторую точку P и провести из неë перпендикуляры к прямым, то основания перпендикуляров, P, X, лежат на одной окружности.
Подсказка 2
Ясно, что можно рассмотреть прямые CI, II_B, II_C, ведь они пересекаются в I и содержат нужные точки. Проведите к отрезкам II_B, II_C перпендикуляры в их серединах. Посмотрите, через какую точку они проходят. Чтобы было проще, можете поискать прямые, параллельные этим перпендикулярам.
Обозначим через середины
и
, через
— середину
. Во-первых, заметим, что
(биссектрисы смежных
углов). Во-вторых, рассмотрим перпендикуляр к прямой
, проведённый в точке
. Он проходит через
. Это нетрудно показать,
нужно лишь заметить, что
(биссектрисы смежных углов), и сделать гомотетию в точке
с коэффициентом
.
Аналогично с перпендикуляром в
. Осталось заметить, что точки
лежат на одной окружности, что и
требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




