Угадай точку
Ошибка.
Попробуйте повторить позже
Две окружности пересекаются в точках и
а
и
— точки касания этих окружностей с их общей касательной
(точка
лежит внутри треугольника
Пусть
— ортоцентр треугольника
Докажите, что угол
прямой.
Подсказка 1
Соберите максимально много информации про рисунок. Обратите внимание на прямую AB, она в треугольнике особенная. Посчитайте угол PBQ.
Подсказка 2
Вероятно, вы пришли к тому, что точки P, H, B, Q лежат на одной окружности. Если нет, то докажите. Если угол ABH прямой, то и смежный с ним угол тоже прямой. Тогда попробуйте сделать пятую точку на окружности, которая поможет нам в решении. Какая это будет точка?
Подсказка 3
Верно, это точка будет A', симметричная A относительно середины PQ(помним, что AB - это радикальная ось окружностей). Теперь осталось только посчитать уголки, и победа.
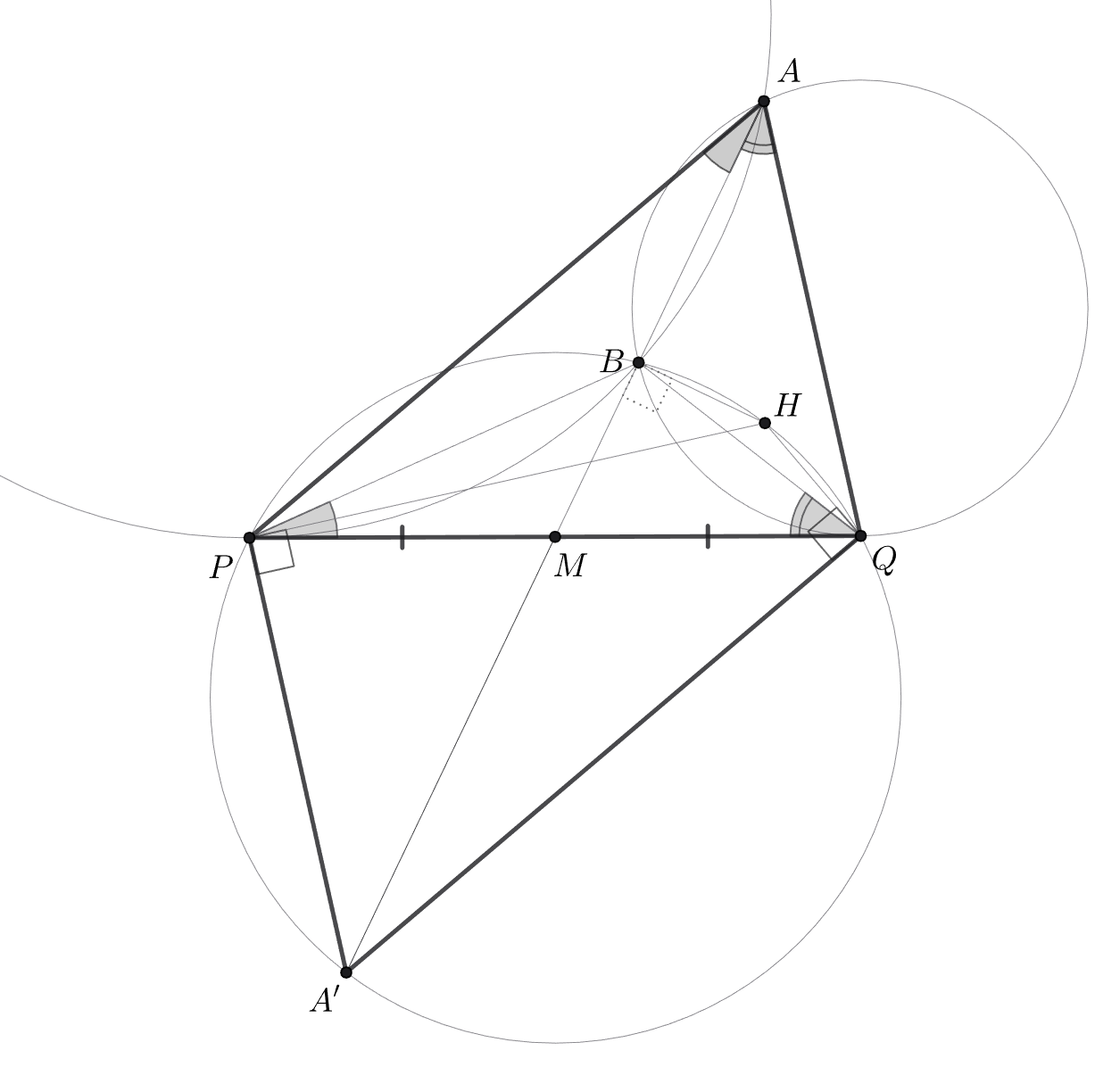
По теореме об угле между хордой и касательной имеем Значит,
Заметим,
что из точки
отрезок
также виден под углом
Таким образом, точки
лежат на одной
окружности.
Прямая — радикальная ось окружностей, а прямая
— их общая касательная. Значит,
проходит через
— середину
Давайте отразим точку
относительно точки
Получим точку
которая также лежит
на окружности
потому что отрезок
виден из неё под углом
но она лежит по другую сторону от
отрезка.
Заметим, что
(чтобы понять, почему это так, достаточно провести высоту Значит,
— диаметр окружности
Отсюда получаем, что
Следовательно, угол
прямой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




