Планиметрия на Турломе
Ошибка.
Попробуйте повторить позже
В ромб 
вписана окружность 
с центром 
Точки 
и 
выбраны на сторонах 
и 
соответственно таким образом,
что 
касается 
в точке 
Обозначим точку касания 
со стороной 
через 
Докажите, что площадь треугольника 
равна площади четырёхугольника 
Источники:
Для начала заметим, что центр вписанной окружности ромба совпадает с центром самого ромба, а значит, является серединой диагонали
. Теперь отметим точки пересечения отрезков 
и 
с отрезком 
: точки 
и 
соответственно. Тогда
вычитая из обеих площадей площадь пятиугольника 
получаем, что нужное нам равенство площадей эквивалентно
равенству
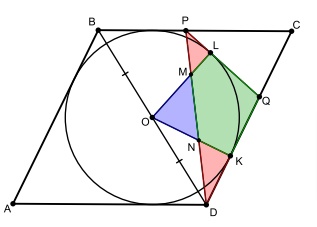
Добавим теперь к обеим частям равенства площади треугольников 
и 
. Получим, что теперь наше равенство выглядит
следующим образом
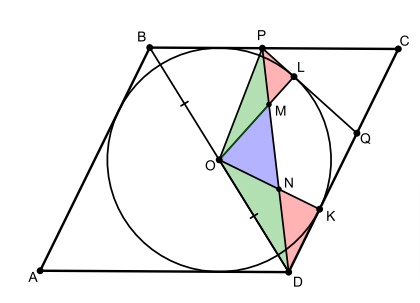
Теперь отметим точку 
касания вписанной в ромб окружности со стороной 
. В силу симметрии относительно диагонали 
треугольники 
и 
равны. А в силу симметрии касательных относительно прямой 
равны треугольники 
и 
(
, очевидно, является биссектрисой угла между касательными, и 
). Тогда наше равенство переходит в
следующее:
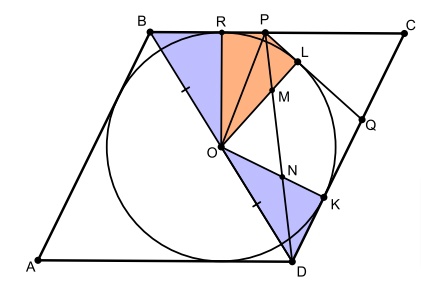
Но площади этих треугольников равны, так как медиана треугольника 
делит его на два равновеликих.
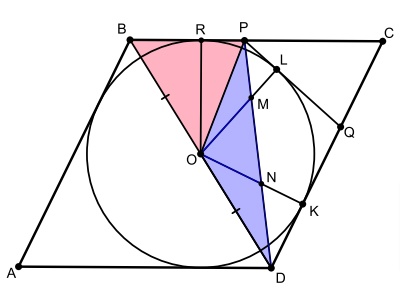
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
