Планиметрия на Турломе
Ошибка.
Попробуйте повторить позже
Пусть 
— центр описанной окружности, 
— точка пересечения медиан остроугольного треугольника 
Прямая,
перпендикулярная 
, проходящая через точку 
пересекает отрезок 
в точке 
Касательная к описанной окружности
треугольника 
в точке 
пересекает прямую 
в точке 
Найдите величину угла 
если 
а
Источники:
Пусть 
— середина стороны 
поскольку 
— медиана, то точки 
лежит на 
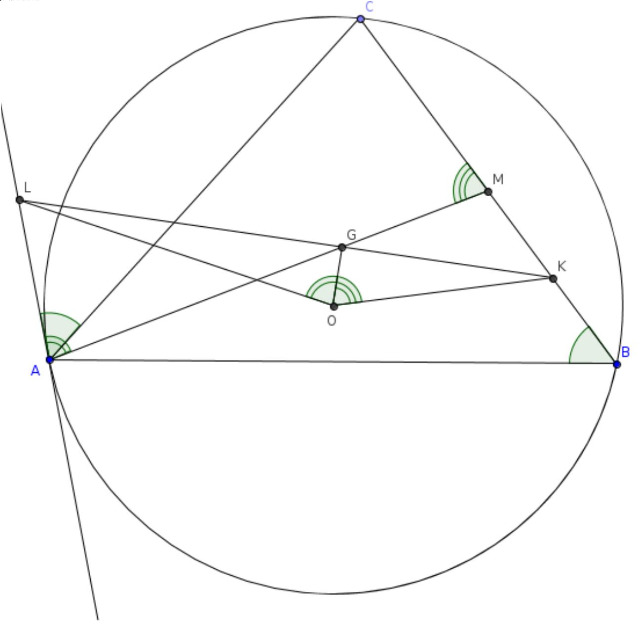
Четырёхугольник 
— вписанный, так как 
(первое равенство по условию, второе следует из того, что
— серединный перпендикуляр к 
), откуда 
Четырёхугольник 
— вписанный, так как 
(первое равенство по условию, второе следует из того, что 
—
радиус, а 
— касательная к описанной окружности треугольника 
), откуда 
Значит,
Первое равенство следует из суммы углов треугольника 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
