Планиметрия на Турломе
Ошибка.
Попробуйте повторить позже
Пусть — центр описанной окружности остроугольного треугольника
На сторонах
и
отмечены точки
и
соответственно. Оказалось, что описанная окружность треугольника
касается прямой
описанная окружность
касается
прямой
а периметр треугольника
равен
Найдите величину угла
Источники:
Подсказка 1
Нужно воспользоваться тем, что BO и СO - касательные. Для этого можно посчитать уголки за счёт теоремы об угле между касательной и хордой. Также за счёт того, что O — центр описанной окружности, мы можем наложить условие на отрезки AO, BO и CO.
Подсказка 2
Отлично! Мы получили, что PB = PO и QO = QC. Пора воспользоваться последним условием на периметр треугольника APQ. Попробуйте записать его и использовать полученные равенства.
Подсказка 3
Сделав это, мы получили, что PQ = PO + OQ. А значит, P, O и Q лежат на одной прямой. Раз так, то мы можем записать условие на то, что ∠POQ развёрнутый. Попробуйте выразить этот угол через ∠BAC.
Подсказка 4
Раз O — центр описанной окружности, то ∠BOC = 2∠BAC. Теперь взглянем на сумму ∠QOC + ∠POB. Выразите её через ∠BAC, используя полученные ранее равенства.
Поскольку описанная окружность треугольника касается прямой
Кроме того, поскольку
— центр
описанной окружности треугольника
откуда
Значит,
откуда
Аналогично,
По условию, то есть
Из предыдущего абзаца мы знаем, что тогда
т.е.
точки
и
лежат на одной прямой.
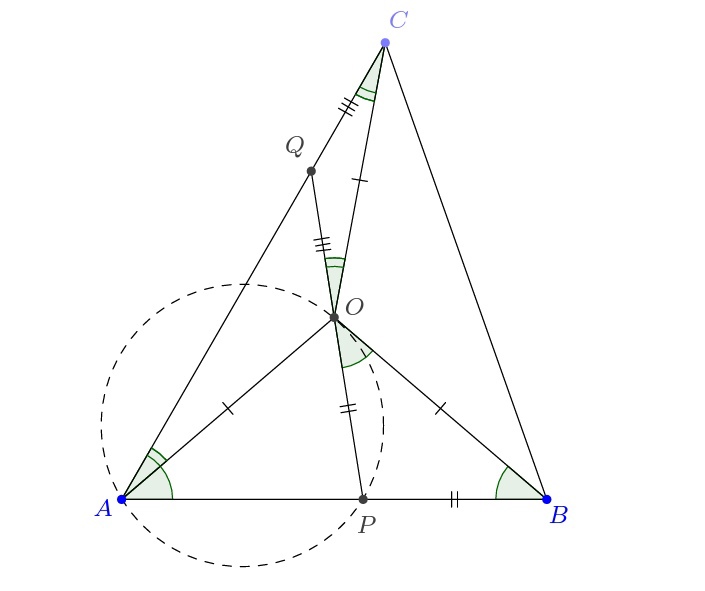
Осталось посчитать уголки. Например, это можно сделать так:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




