Текстовые задачи на ДВИ

Изобразим условие задачи в координатах по времени и положению в пространстве. Пусть точка соответствует нахождению в пункте А в автомобиль выехал из нее и прибыл в пункт Б, пусть это произошло в точке Проехав пути, водитель заметил, что в сторону пункта А выехал велосипедист. Обозначим эту точку за Пусть расстояние от A до Б равно тогда В то же время, что автомобиль прибыл в пункт Б, из пункта Б выехал автобус в пункт А. Следовательно, момент выезда автобуса соответствует точке Автобус прибыл в пункт А в пусть это будет точка Когда автобусу оставалось проехать пути, он поравнялся с велосипедистом, обозначим эту точку за Пусть расстояние от A до B равно тогда Продлим прямую до пересечения с осью в точке

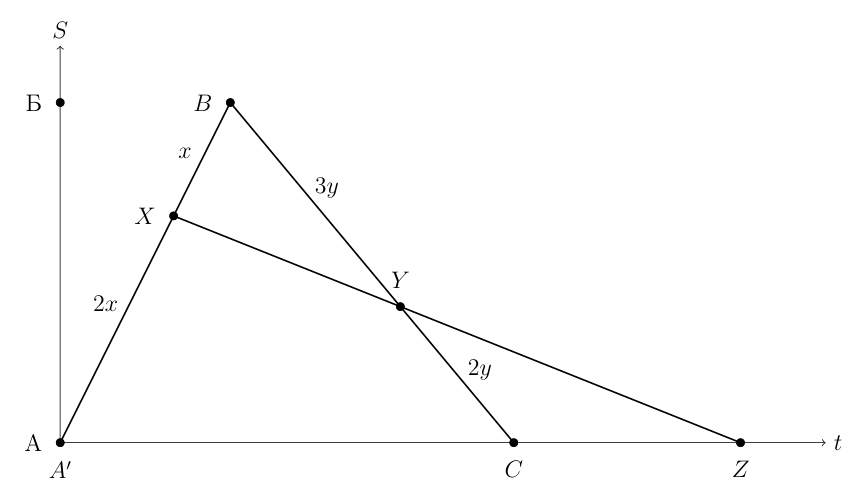
Точка будет соответствовать прибытию велосипедиста в пункт A, так как он двигался с постоянной скоростью. Рассмотрим треугольник и прямую По теореме Менелая

Получим, что

Поскольку точка соответствует точка — выходит, что точка будет соответствовать