Параметры на ДВИ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра 
, при каждом из которых уравнение
имеет единственное решение.
Источники:
Подсказка 1
Пугающая штука… Что может нам помочь?) Симметрии на первый взгляд не видно, идея напрямую выражать корни тоже как будто бы не вдохновляет, остаётся только упрощать то что видим.
Подсказка 2
Выведите слагаемое с параметром в одну сторону, а всё остальное – в другую. Удаётся ли разложить на скобки что-то из подкоренных выражений? А может быть где-то можно вообще вынести множитель из под корня?)
Подсказка 3
Удастся ли нам оставить в левой части только параметр (может быть с каким-то числовым множителем), а всё остальные вывести вправо? Если корень-множитель не равен нулю, то смело можем на него поделить!
Подсказка 4
Попробуйте ввести замену так, чтобы перед нами в итоге осталось квадратное уравнение с параметром! После хорошего исследования замены добить задачу будет не так уж трудно!
Подсказка 5
Если замену не удаётся увидеть, то покажем вам её: t = (¹⁰√((x + 4)(x + 3))/(⁵√(x + 3))
Подсказка 6
Аккуратненько разберём, чем является наше t? Не забывайте, его знаменатель не всегда положителен, поэтому ошибкой будет сразу же сокращать кажущиеся похожими множители! А в целом исследование удобно начать с рассмотрения случаев и работы с подкоренным выражением в итоге!
Подсказка 7
Итак, у нас есть два случая. Под корнем 10-й степени в обоих этих случаях одно и то же выражение. Давайте изобразим его график и сделаем выводы: сколько значений этого выражения соответствуют каждому х? Какие они могут быть?
Подсказка 8
Распространите выводы, сделанные выше, на саму t. Теперь мы знаем, при каких значениях t существуют соответствующие значения х. Осталось понять – когда квадратное уравнение, полученное выше, имеет ровно одно решение в полученном промежутке. Это удобно сделать графическим методом, предварительно заменив всю левую часть на какую-нибудь одну букву (14а² = b)
Пусть 
, тогда уравнение имеет вид
Так как 
не является решением уравнения, то можно разделить обе части равенства на 
, получим
_________________________________________________________________________________________________________________________________________________________________________________
Заметим, что 
, так как 
может быть как положительным, так и отрицательным.
_________________________________________________________________________________________________________________________________________________________________________________
Сделаем замену 
, тогда 
, следовательно, уравнение примет вид
Исследуем замену:
Если обозначить 
— убывающая функция, то
Изобразим график функции 
:
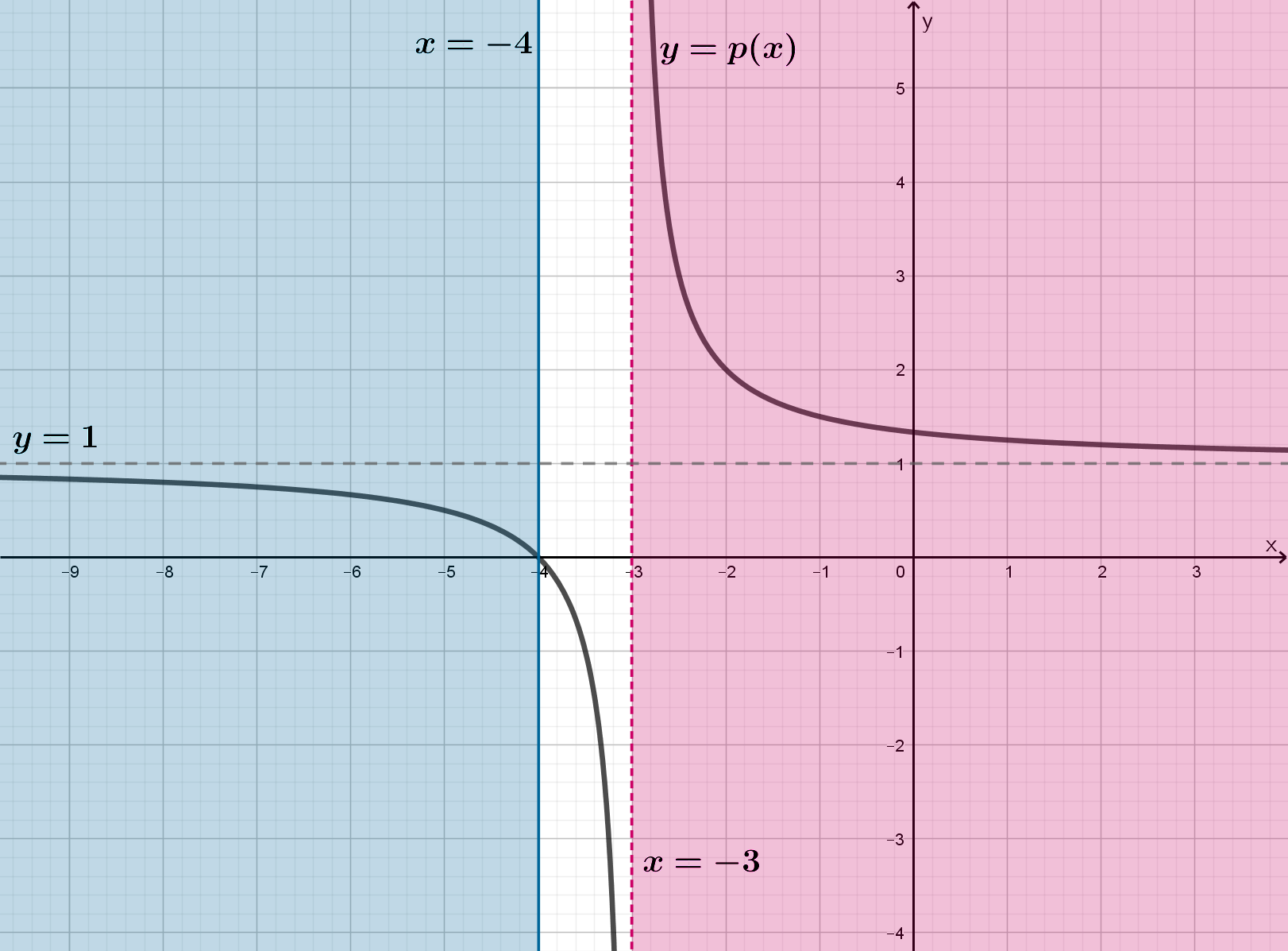
Заметим, что одному значению 
(из области значений) соответствует ровно одно значение 
При 
функция 
принимает значения от 
до 
, значит, 
принимает значения от 
до
.
При ![x∈ (−∞;− 4]](/api/latex-service/v1/GetSession/65166/index-9f6e9e74fbd6b9ebe2c0d30ea9f05d55.svg)
функция 
принимает значения от 
до 
, значит, 
принимает значения от 
до
.
Следовательно, график 
выглядит следующим образом (
и 
— горизонтальные асимптоты):
Значит, область значений ![t∈ (− 1;0]∪(1;+ ∞)](/api/latex-service/v1/GetSession/65166/index-95ba2fa4ae8ef5b2ec0a764c8f5a38fb.svg)
, причем заметим, что одному значению 
(из области значений) соответствует ровно
одно значение 
.
Изобразим график функции 
при ![t∈ (−1;0]∪(1;+∞)](/api/latex-service/v1/GetSession/65166/index-7cc25d2e6243ec799ede205d196caae0.svg)
в системе координат 
и найдем такие положения
горизонтальной прямой 
, при которых она с графиком функции 
имеет ровно одну точку пересечения:
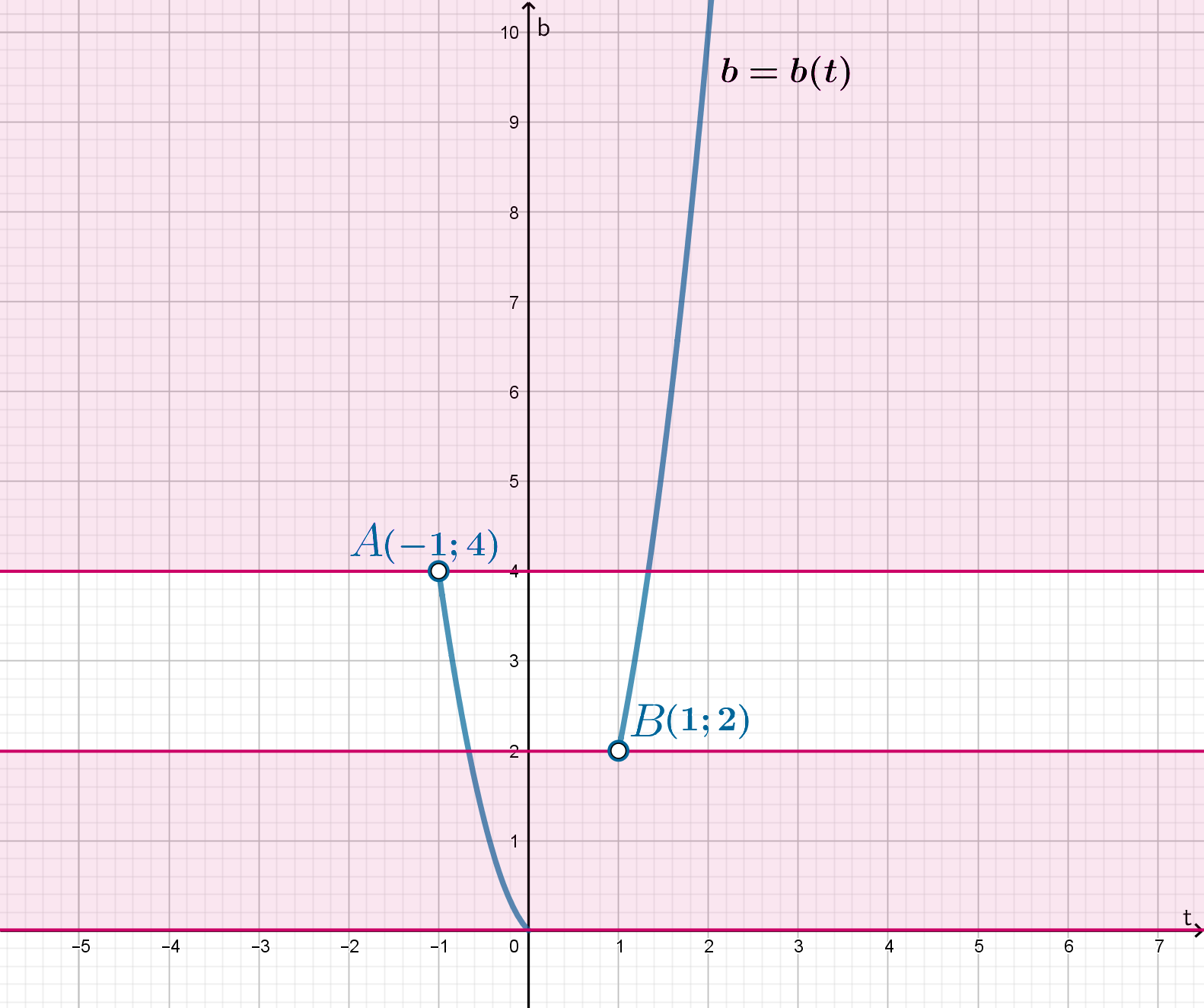
Следовательно,
![⌊ ⌊ 2 1 ( ∘--] [ ∘--∘ -] [∘-- )
⌈ b∈[0;2] ⇒ ||a ≤ 7 ⇔ a∈ −∞; − 2 ∪ − 1; 1 ∪ 2;+ ∞
b≥4 ⌈a2 ≥ 2 7 7 7 7
7](/api/latex-service/v1/GetSession/65166/index-954c251a6c500361c2ebaa976171d4c4.svg)
_____________________________________________________________________________________
Графики функций 
и 
рисовать было необязательно, они изображены лишь для наглядности области значений
функций.
![( ∘-2] [ ∘ 1-∘ 1] [∘-2 )
−∞;− 7 ∪ − 7; 7 ∪ 7;+ ∞](/api/latex-service/v1/GetSession/65165/index-ae45d800042177ada289f3a7ad8965be.svg)
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
