18.01 Робот-сборщик – базовые задания
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клетки. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение
одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку,
по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Для приведенного ниже квадрата определите минимальную денежную сумму и максимальную денежную
сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа
друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную сумму. Для вашего
удобства таблица была прикреплена в виде файла.
Заполним новую таблицу начиная с левой нижней клетки. Далее для каждой ячейки будем брать сумму той же ячейки из исходной таблицы и минимальное/максимальное из клеток слева и снизу новой таблицы.
Минимум:
Первым ответом получаем .
Максимум:
Вторым ответом будет .
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за
одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите минимальную денежную сумму и максимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную сумму.
Исходные данные представляют собой электронную таблицу размером N N, каждая ячейка которой соответствует
клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
Исходная таблица:
Заполним новую таблицу начиная с левой нижней клетки. Далее для каждой ячейки будем брать сумму той же ячейки из исходной таблицы и минимальное/максимальное из клеток слева и снизу новой таблицы.
Минимум:
Первым ответом получаем 1059.
Максимум:
Вторым ответом будет 2216.
Ошибка.
Попробуйте повторить позже
Задание выполняется с использованием прилагаемых файлов.
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
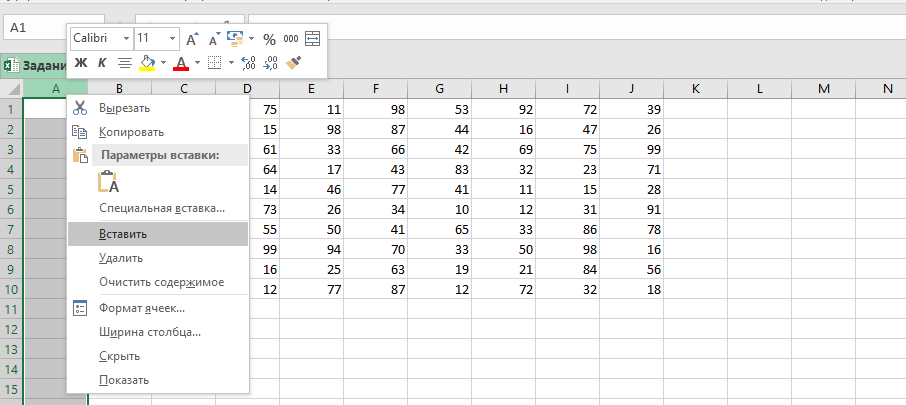
Выделим всю таблицу и добавим границы.
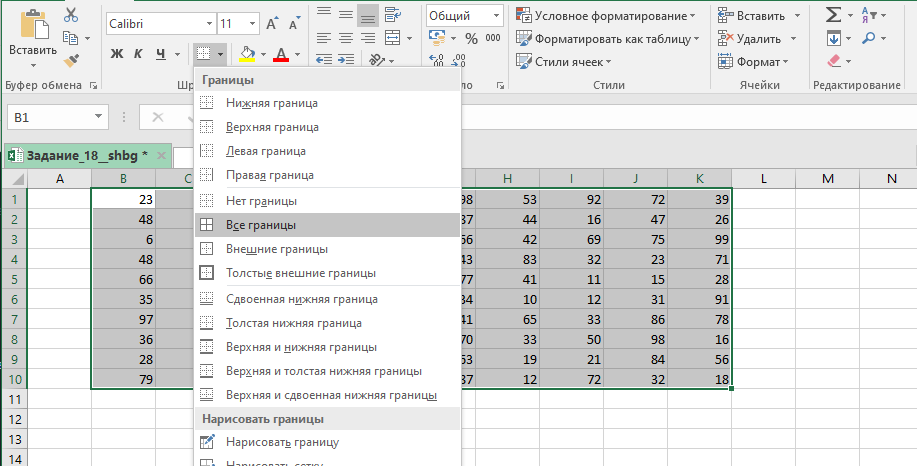
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(C12;B13)+С1

Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки. Заменим все МИН на МАКС.
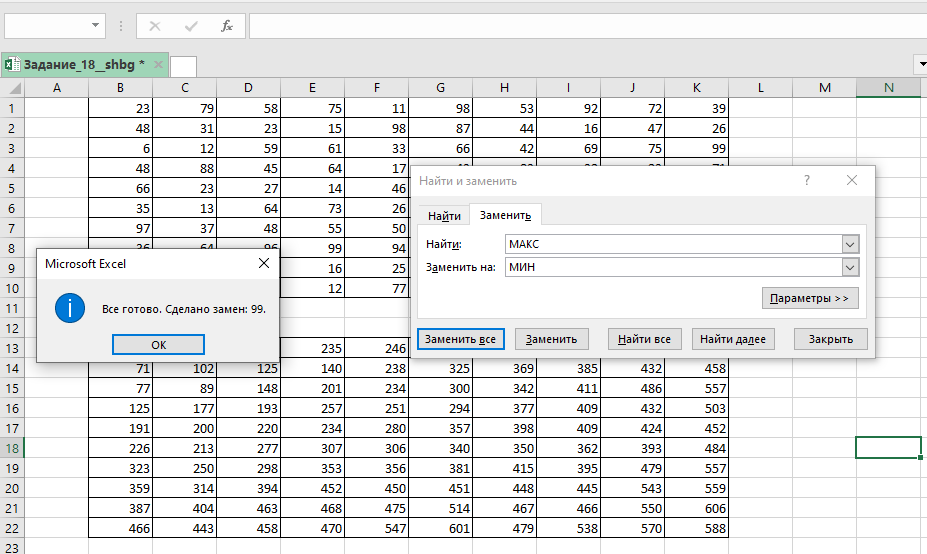
Запишем в ответ сначала максимальное количество монет, затем - минимальное (без разделительных знаков).
Ошибка.
Попробуйте повторить позже
Дан квадрат клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата
стоит робот. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо
вниз. Выходить за пределы квадрата робот не может. Определите максимальную и минимальную сумму
чисел в клетках, которую может собрать Робот (включая начальную и конечную клетки), пройдя из левой
верхней клетки в правую нижнюю. В ответе укажите одно число – сумму максимальной и минимальной
сумм.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
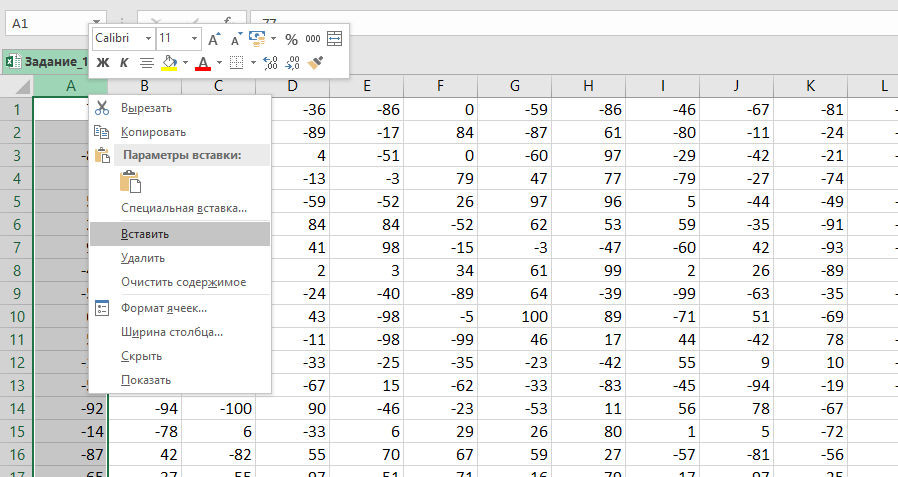
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(C22;B23;B22)+C1
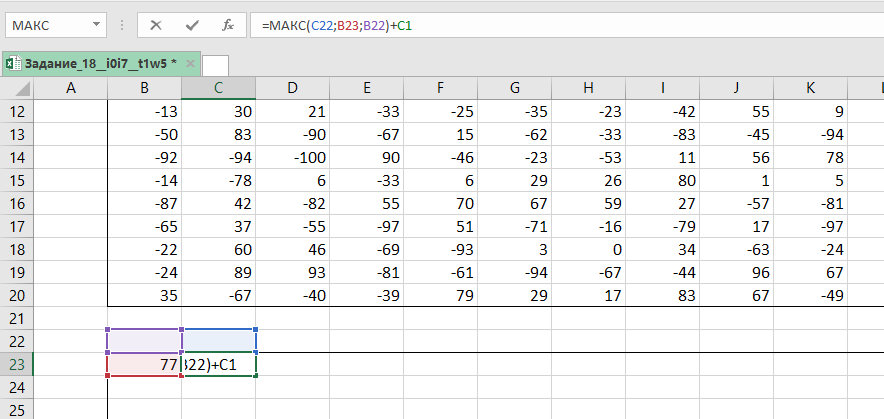
Копируем её на всю таблицу. Выписываем 1909 из правой нижней ячейки. Заменим все МИН на МАКС.
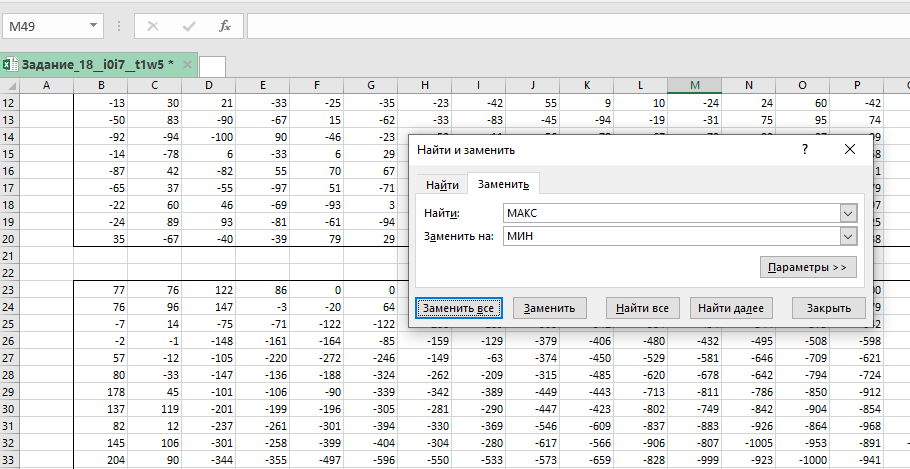
В правой нижней ячейке получим -1473.
Запишем в ответ сумму двух полученных значений: 1909 + (-1473) = 436.
Ошибка.
Попробуйте повторить позже
Дан квадрат клеток, в каждой клетке которого записано целое число. В левом верхнем углу стоит некая фигура.
За один ход она может переместиться в пределах квадрата либо вправо (на одну или две клетки), либо вниз (на одну или
две клетки). Необходимо переместить фигуру в правый нижний угол так, чтобы сумма чисел в клетках, в которых она
останавливалась (включая начальную и конечную), была максимальной.
В ответ запишите максимально возможную сумму.
Добавляем 2 пустых столбца (выделяем столбцы и
, нажимаем правой кнопкой и выбираем Вставить).
Выделим всю таблицу и добавим границы.
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(D22;D23;C24;B24)+D1
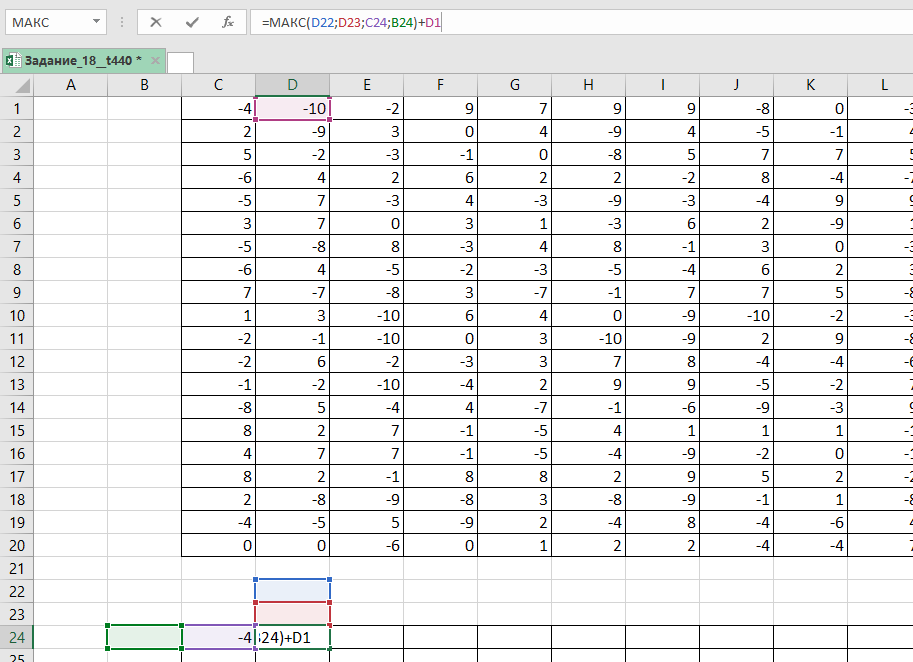
Копируем её на всю таблицу.
Выписываем значение из правой нижней ячейки в ответ.
Ошибка.
Попробуйте повторить позже
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на клеток
. Робот стоит в левом нижнем углу. Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо
Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу
квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до
. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите минимальную денежную сумму и максимальную денежную сумму, которую может собрать Робот. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную сумму.
Исходные данные представляют собой электронную таблицу размером , каждая ячейка которой соответствует
клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
Скопируем табличку вниз. Очистим ее. Вставим левое нижнее число из изначальной ячейки.
Далее левую сторону и нижнюю заполняем как: предыдущее значение + значение из старой ячейки.
Потом встаем в ячейку по диагонали вправо вверх и пишем основную формулу для подсчета:
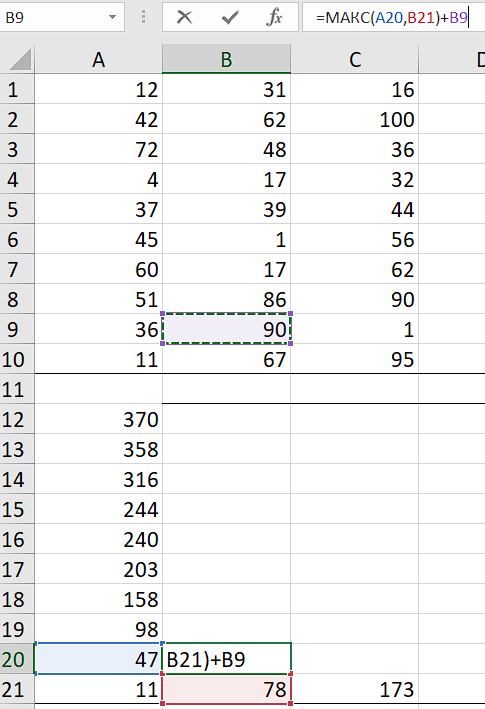
Также поступаем с минимальной суммой - заменяем в формулах на МИН. Пишем ответ.
Ошибка.
Попробуйте повторить позже
Задание выполняется с использованием прилагаемых файлов.
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом через пробел — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером , каждая ячейка которой соответствует
клетке квадрата.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить) и пустую строку перед
самой первой (нажимаем правой кнопкой мыши на строку
и выбираем Вставить).
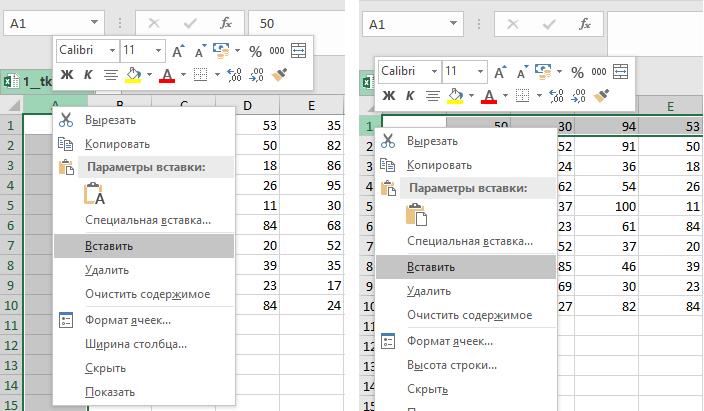
Выделим всю таблицу и добавим границы.
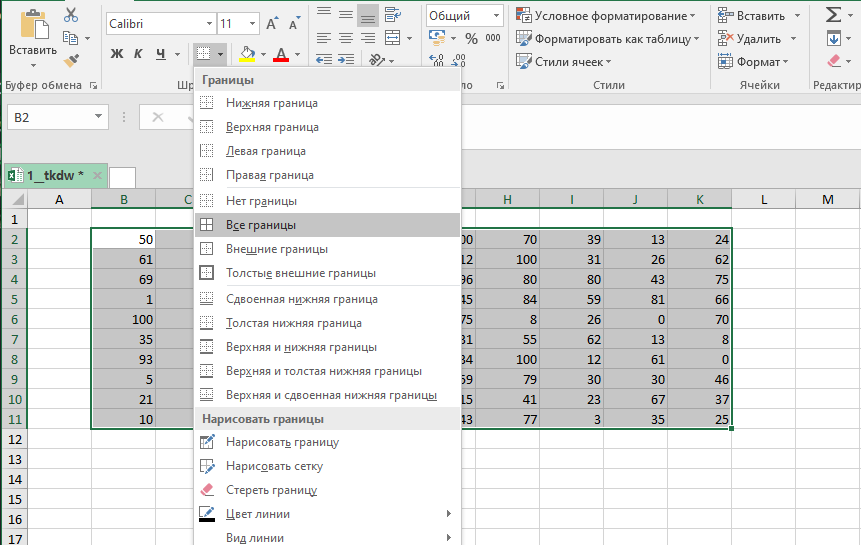
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =C2+МАКС(B14;C13)
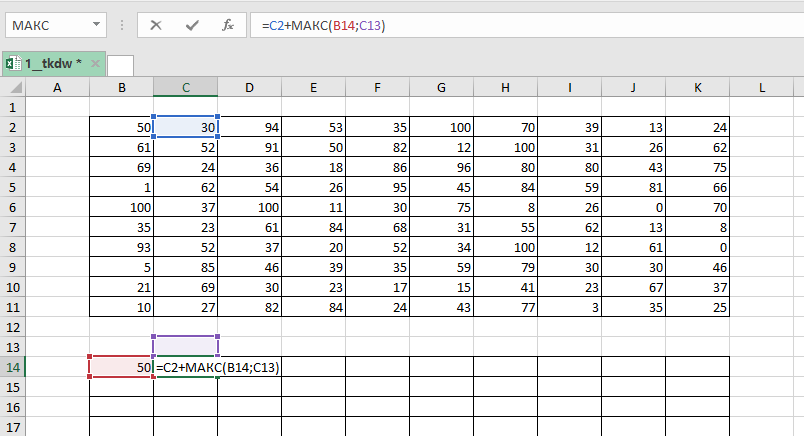
Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки. Заменим все МИН на МАКС.
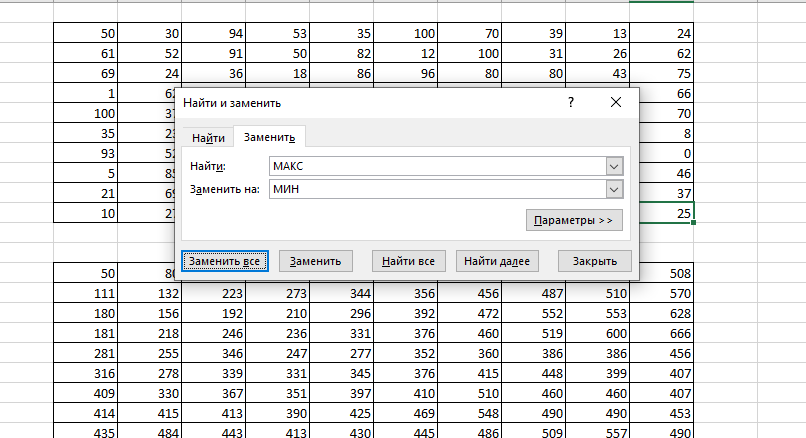
Запишем в ответ сначала максимальное количество монет, затем через пробел - минимальное.
Ошибка.
Попробуйте повторить позже
Задание выполняется с использованием прилагаемых файлов.
Квадрат разлинован на клеток
. В каждой клетке записано целое положительное число.
Исполнитель Робот имеет несколько команд: вправо, вверх и диагональ, которые, соответственно, перемещают его
на одну клетку вправо, на одну клетку вверх, на одну клетку по диагонали, двигаясь в правый верхний
угол.
Робот двигается только в рамках поля, при выходе за границу робот уничтожается. Начало движения робота — левая нижняя клетка, конец — верхняя правая клетка. При прохождении клетки к счету Робота прибавляется число, записанное в соответствующей ячейки таблицы.
Какой максимальный и минимальный счет может быть получен в результате работы исполнителя? В ответе запишите два числа — сначала максимально возможный счет Робота, затем минимальный.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
Выделяем всю таблицу и добавляем границы.

Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой нижней клетки данной нам таблицы. В клетку
записываем формулу =C12+МАКС(B27;B28;C28)
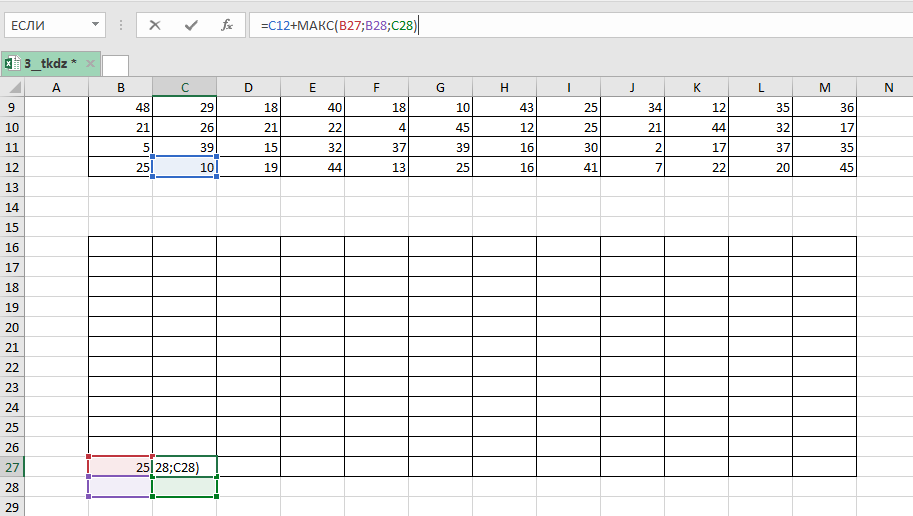
Копируем её на всю таблицу.
Выписываем значение из правой верхней ячейки.
Заменим все МАКС на МИН и также выпишем значение из правой верхней клетки.

Запишем в ответ сначала максимальный счёт, затем через пробел - минимальный.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив
клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
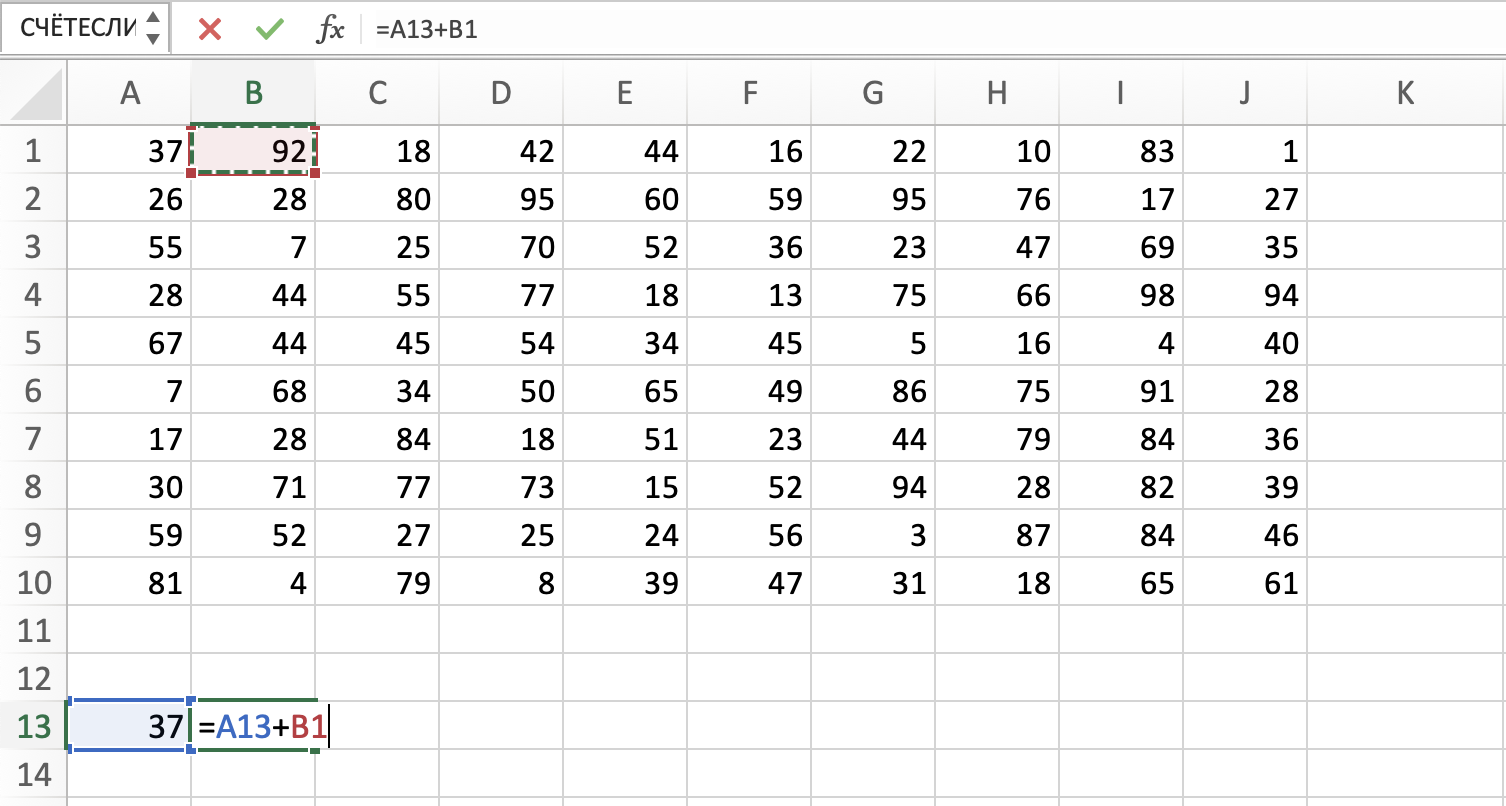
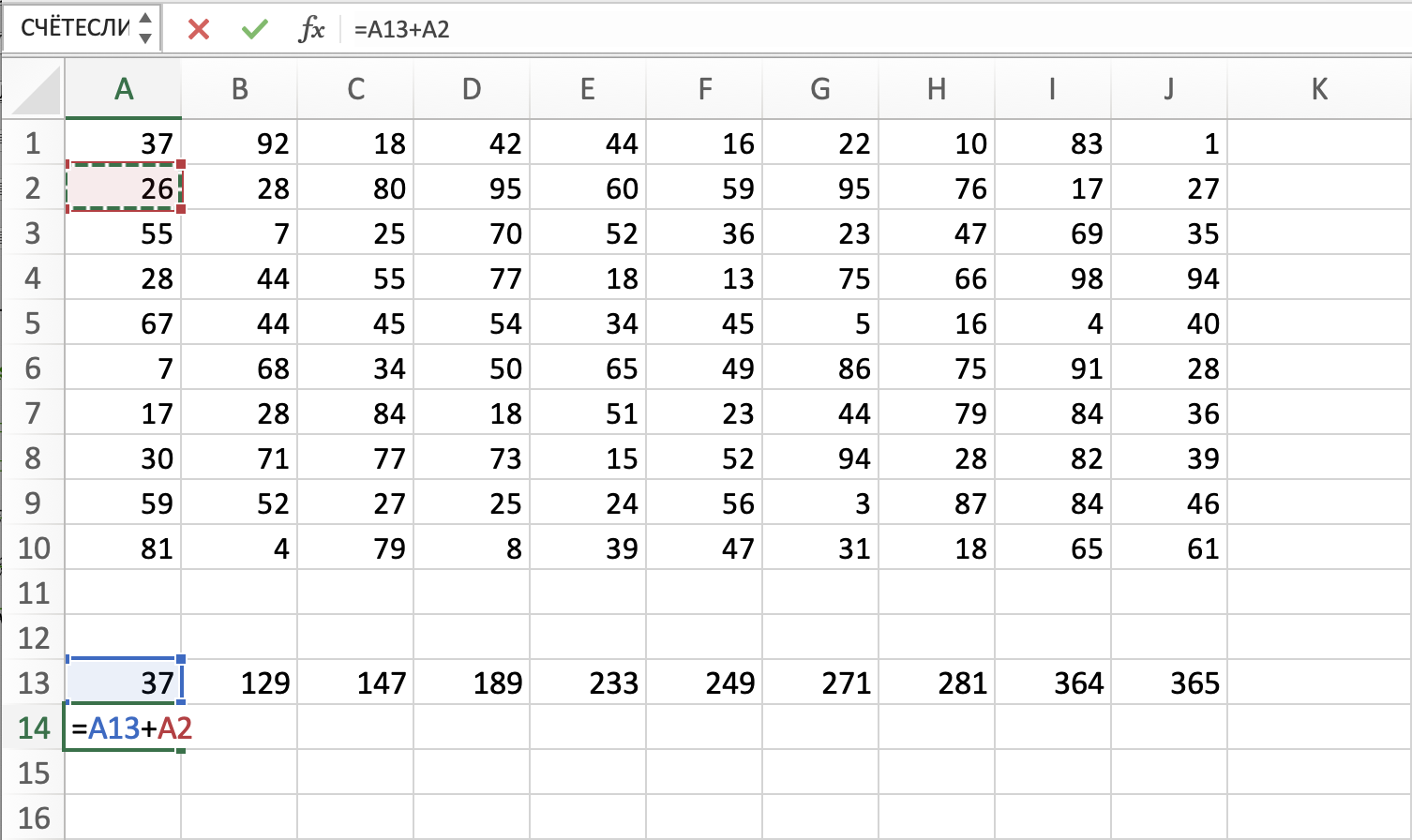
Открываем файл с таблицей. Чуть ниже основной таблицы начинаем создавать свою, в которой будем производить все
вычисления. Так как робот идет из верхней левой в правую нижнюю клетку, то переписываем верхнюю левую ячейку
без измнений. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к
изначальному значению ячейки предыдущее. Растягиваем формулу на всю строку и на весь столбец.

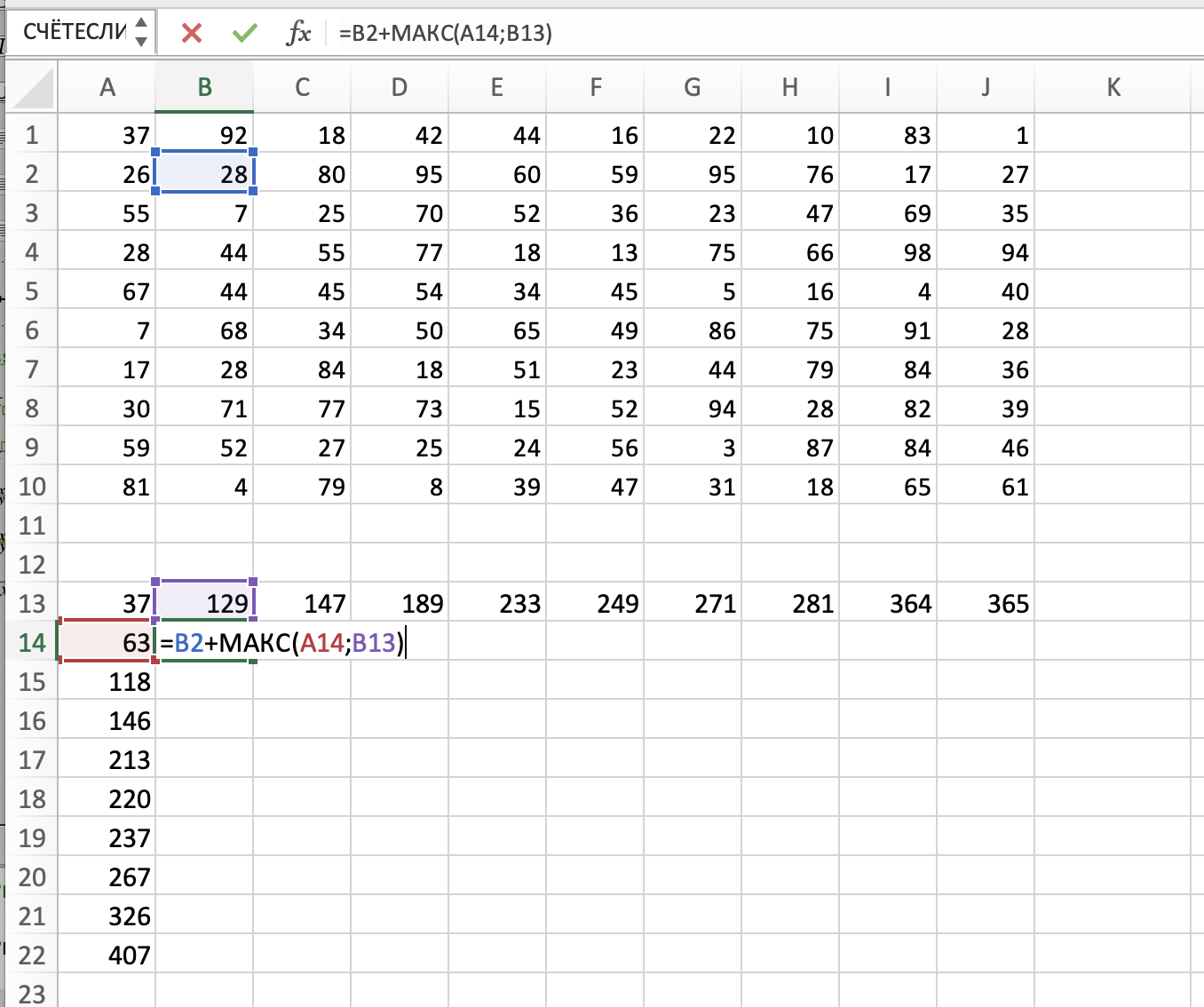
Затем в ячейке В14 пишем следующую формулу:
=В2+МАКС(А14;В13).
Она выбирает максимальное значение из ячеек В13 и А14, а потом прибавляет к изначальным монеткам. Растягиваем эту формулу на диапазон В14:J22. В правой нижней ячейке J22 и будет искомая максимальная сумма. Она равна 1325.

Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН:
=В2+МИН(А14;В13).
Минимальная сумма равна 596.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную.
Открываем файл с таблицей. Чуть ниже основной таблицы начинаем создавать свою, в которой будем производить все
вычисления. Так как робот идет из левой нижней в правую верхнюю клетку, то переписываем нижнюю левую ячейку
без измнений. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к
изначальному значению ячейки предыдущее. Растягиваем формулу на всю строку и на весь столбец.

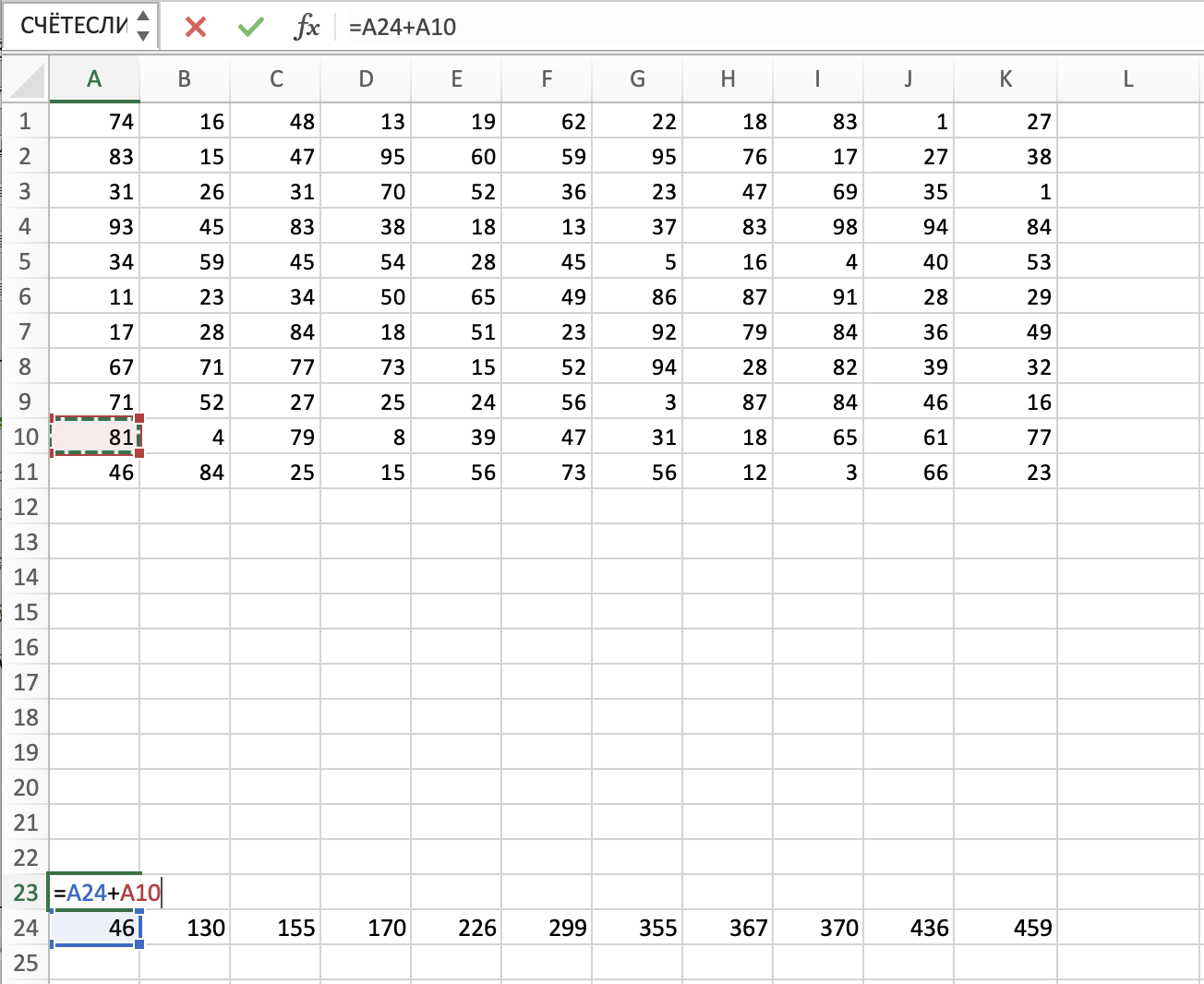
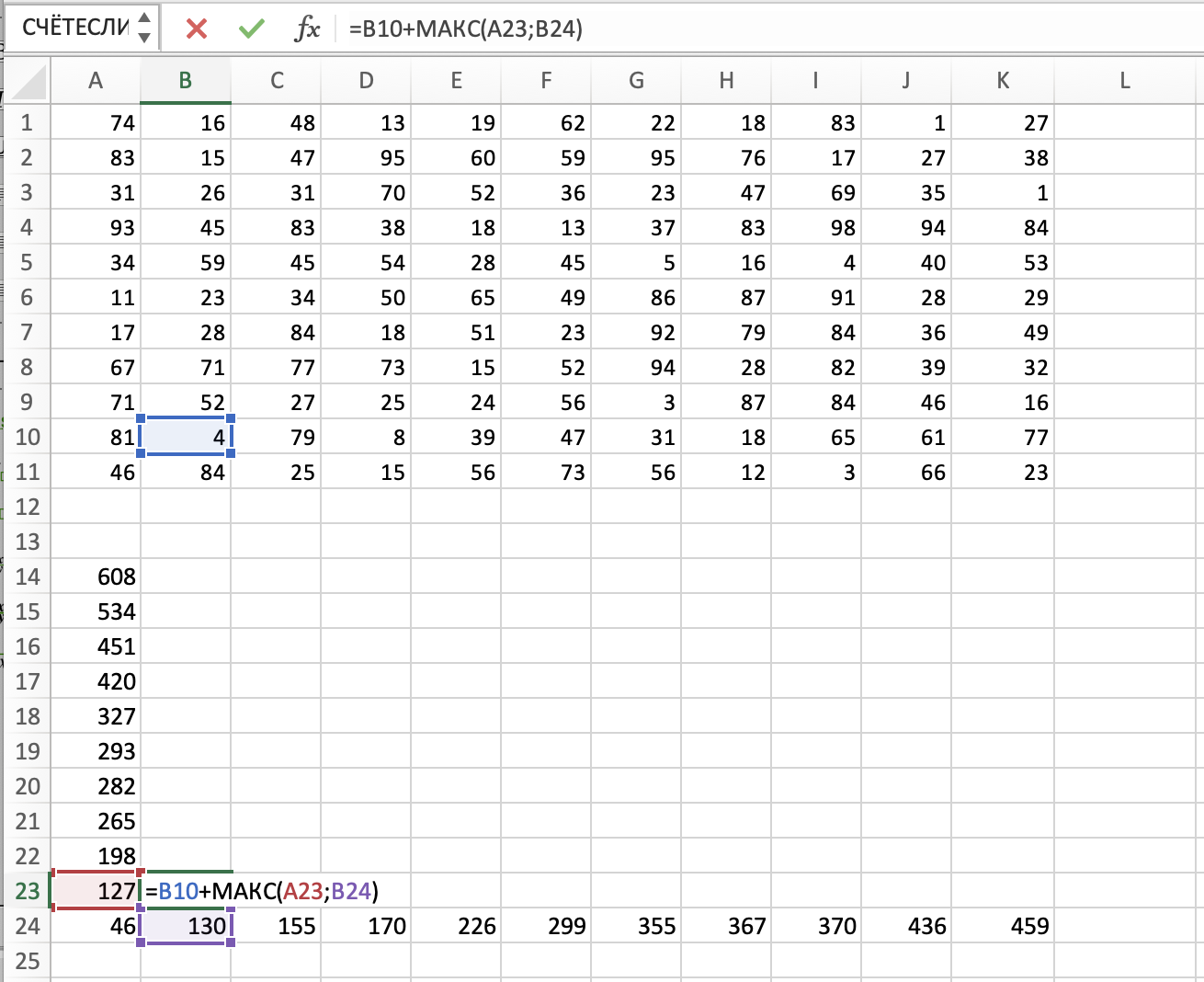
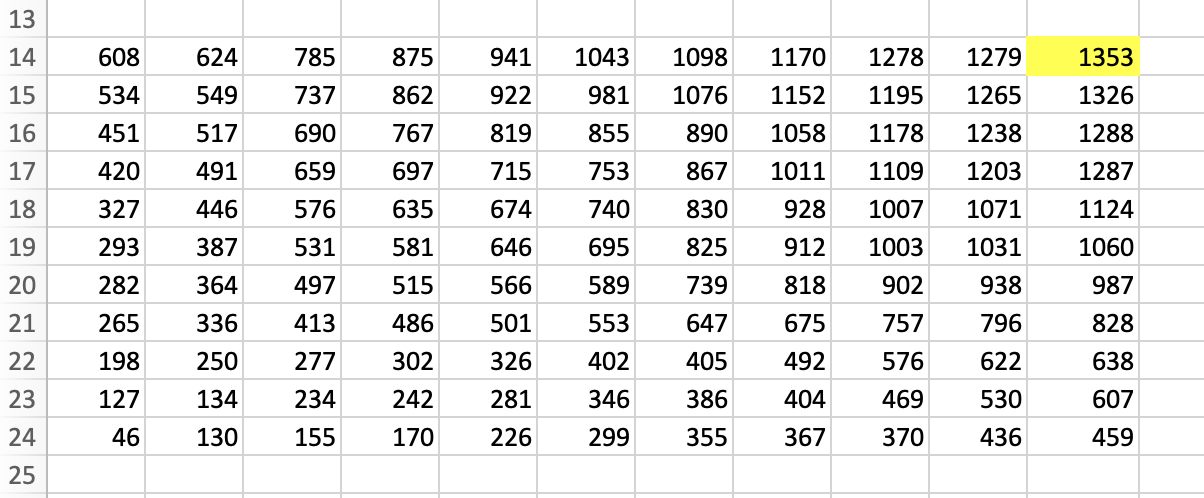
Затем в ячейке В23 пишем следующую формулу:
=В10+МАКС(А23;В24).
Она выбирает максимальное значение из ячеек В14 и А15, а потом прибавляет к изначальным монеткам. Растягиваем эту
формулу на диапазон В23:K14. В правой верхней ячейке К14 и будет искомая максимальная сумма. Она равна
1353.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН:
=В10+МИН(А23;В24).
Минимальная сумма равна 659.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
1) Выделяем таблицу, копируем её и вставляем рядышком. Рамками обозначаем границы.
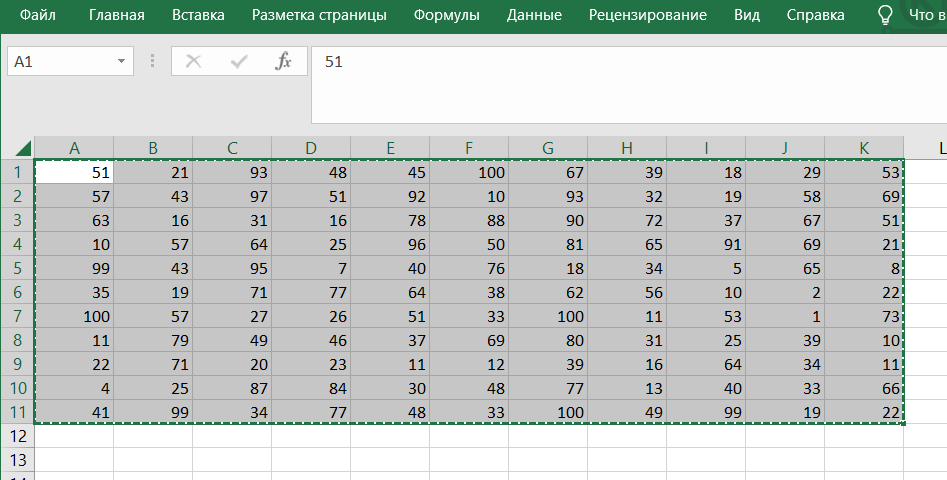
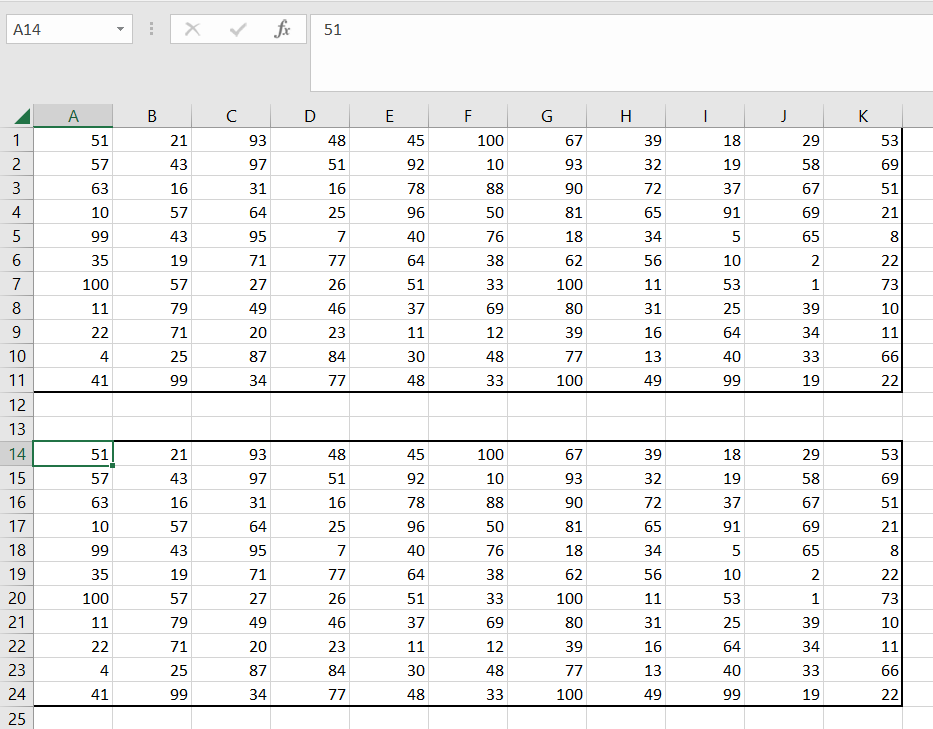
2) Выделяем новую таблицу, очищаем её клавишей delete.
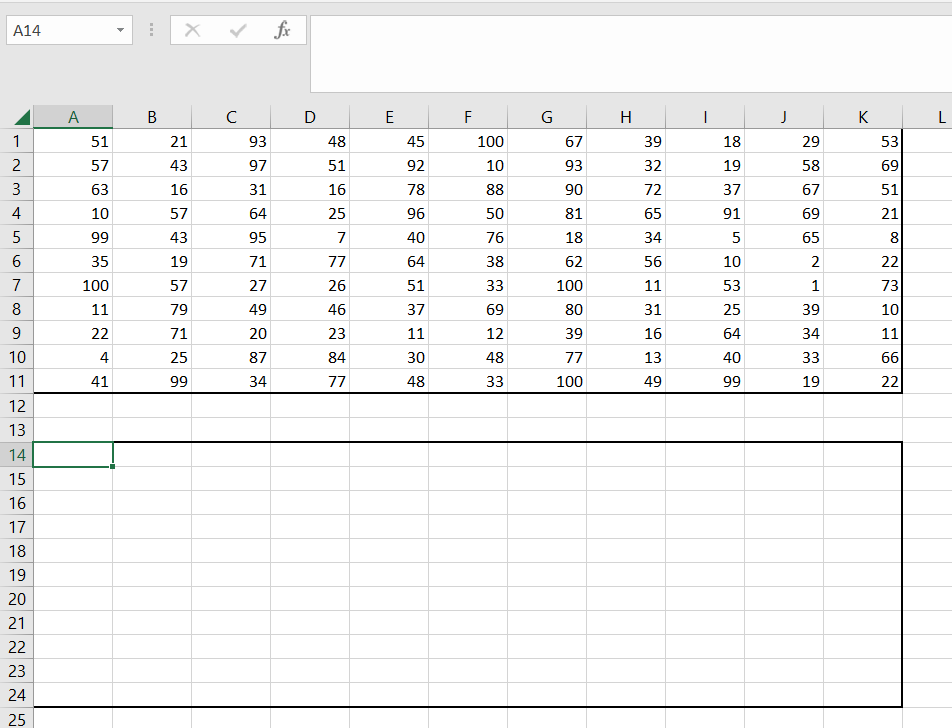
3) Начало с левой нижней клетки, поэтому приравниваем ей значение с левой нижней клетки изначальной таблицы.
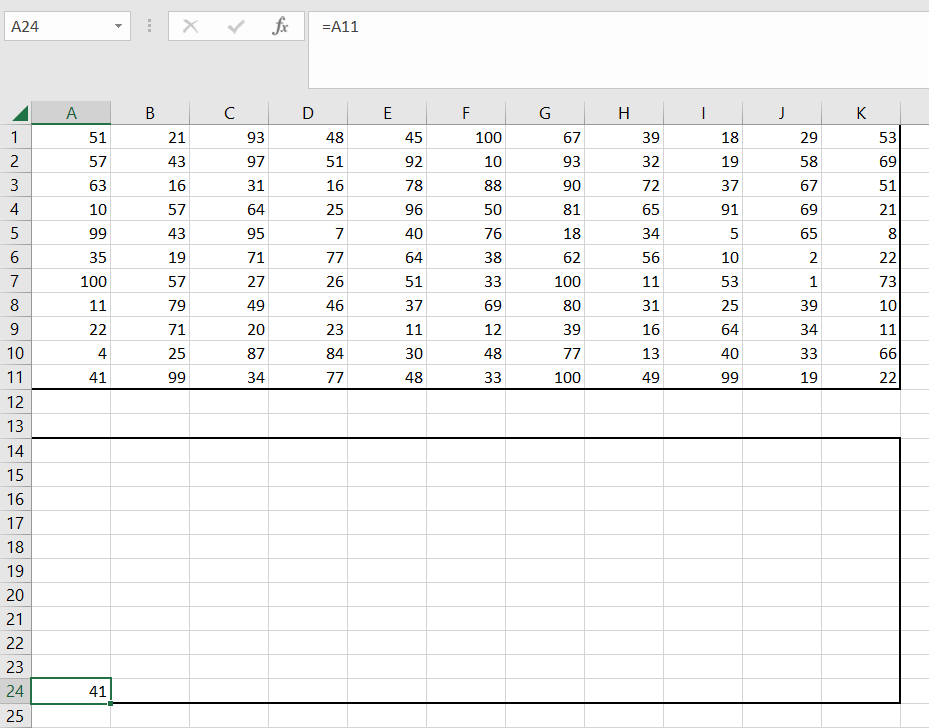
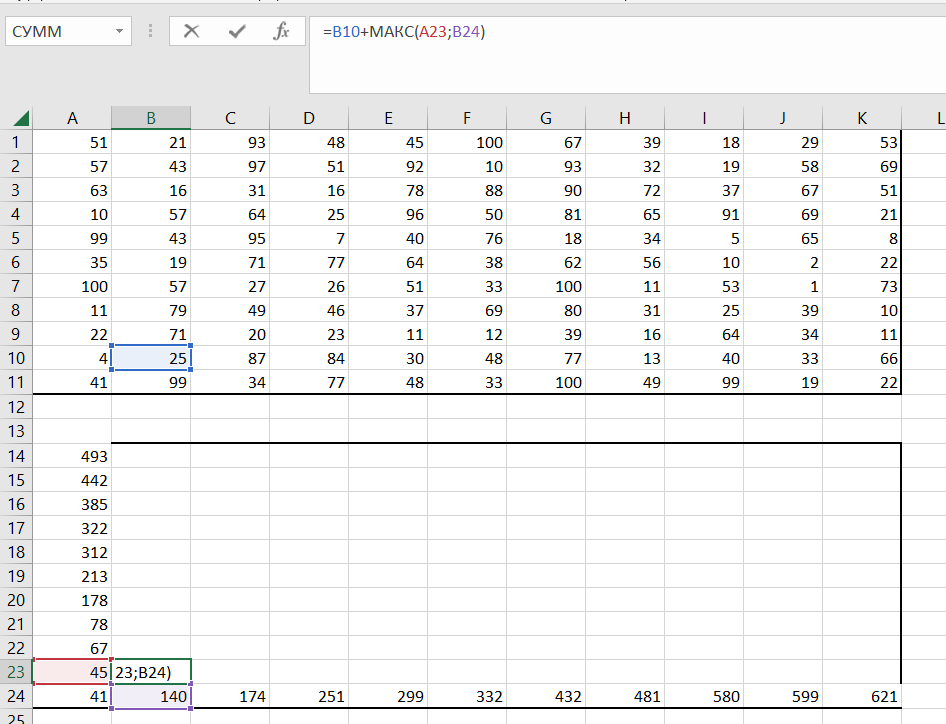
4) В клетках сверху и справа записываем сумму текущего значения(из аналогичной клетки с первой таблицы) и предыдущего. Растягиваем ячейки до границ (удерживая квадратик на уголке ячейки).

5) В клетке с расположением по диагонали записываем сумму значения из аналогичной клетки и макс. числа среди клеток, из которых можно попасть в эту клетку. Растягиваем ячейку по всей таблице, в правом верхнем углу получаем первое число.
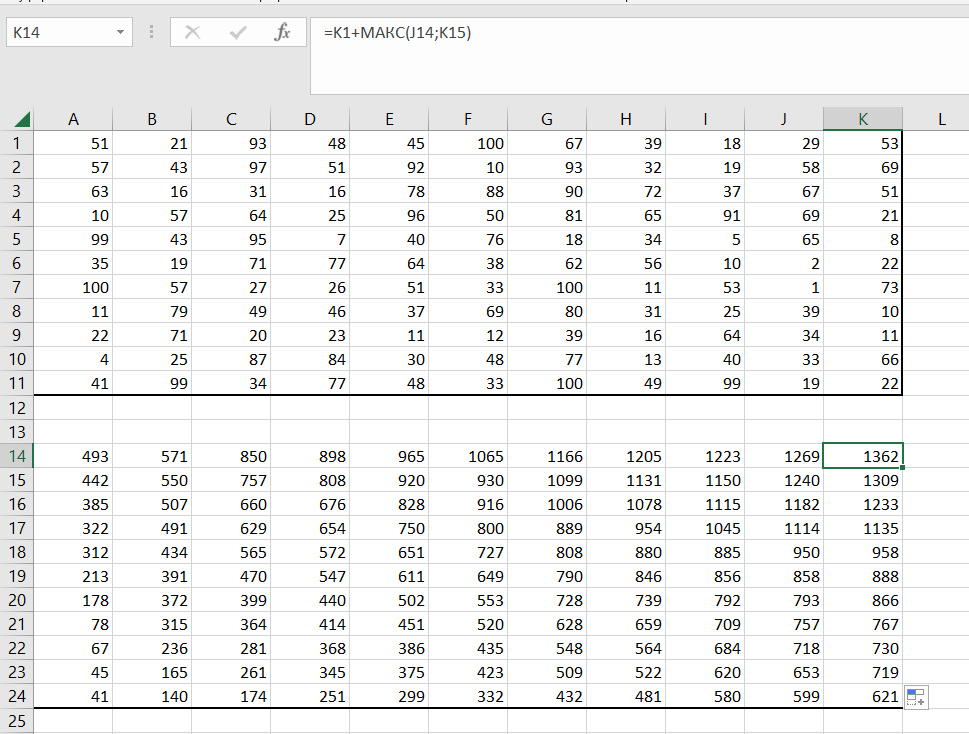
6) С помощью комбинации клавиш Ctrl+F открываем окно поиска, заходим в «Заменить», записываем в первую строку «МАКС», во вторую «МИН», далее нажимаем «Заменить всё». В правой верхней клетке теперь содержится минимальная сумма.
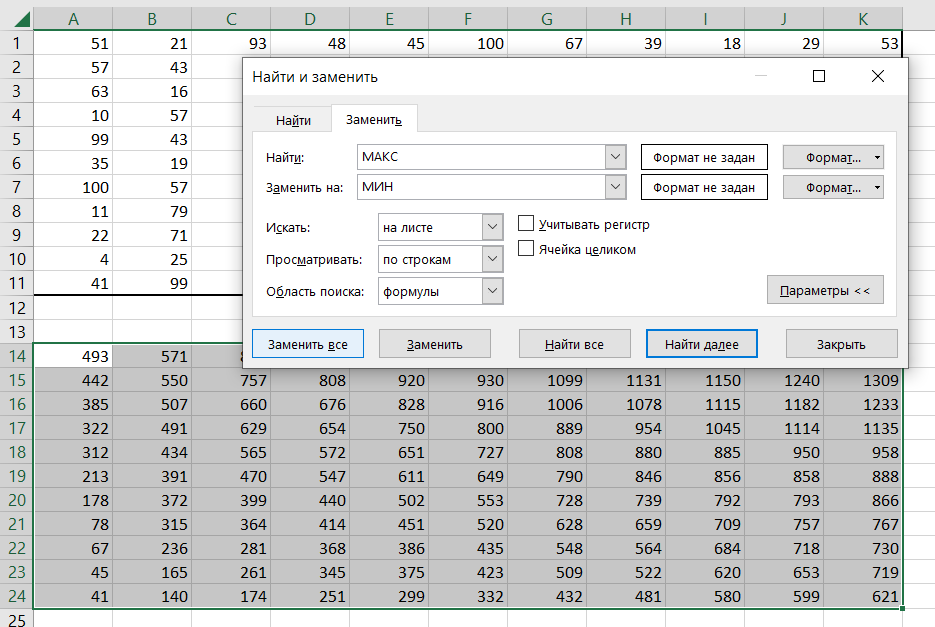
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз – в соседнюю нижнюю. При попытке пересечь границы Робот разрушается. Перед
каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив
клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков – сначала максимальную сумму, затем минимальную.
Нам дано поле 13 на 13, создадим рядом еще одно поле такого же размера (ячейки ) . В левую верхнюю
клетку нового поля, записываем значение из левой верхней клетки исходного поля – 44.
Сначала заполним значениями верхнюю строку. Для этого к значению из левой верхней клетки нового поля,
прибавим значение из клетки , сделаем это с помощью формулы:
=A15+B1
Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.
Найдем максимальное значение суммы. Рассмотрим ячейку , в нее мы можем попасть из
и
, тогда,
чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из
которых можем попасть в эту. В ячейку
запишем формулу:
=МАКС(A16;B15)+B2
Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальной суммой, которую может собрать робот.
Для минимальной суммы порядок действий аналогичный, только формула в будет выглядеть так:
=МИН(A16;B15)+B2
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: влево или вверх. По команде влево Робот перемещается в соседнюю левую
клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед
каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив
клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из правой нижней клетки в левую верхнюю. В ответ запишите два числа через пробел — сначала максимальную сумму, затем минимальную.
1. Открываем файл с таблицей.
2. Чуть ниже основной таблицы начинаем создавать свою, в которой будем производить все вычисления.
3. Так как робот идет из нижней правой в левую верхнюю клетку, то переписываем нижнюю правую ячейку без измнений в ячейку J22.
4. Затем прописываем формулу для первой строки =J22+I10 и для первого столбца = J22+J9. Мы прибавляем к изначальному значению ячейки предыдущее. Растягиваем формулу на всю строку и на весь столбец.
5. Затем в ячейке I21 пишем следующую формулу:
=I9+МАКС(I22;J21).
Она выбирает максимальное значение из ячеек J22 и J21, а потом прибавляет к изначальным монеткам. Растягиваем эту
формула на диапазон I21:A13. В левой верхней ячейке А13 и будет искомая максимальная сумма. Она равна
1307.
6. Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН:
=I9+МИН(I22;J21).
Минимальная сумма равна 658.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз – в соседнюю нижнюю. При попытке пересечь границы Робот разрушается Перед
каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив
клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков – сначала максимальную сумму, затем минимальную.
Нам дано поле 13 на 13, создадим рядом еще одно поле такого же размера (ячейки ) . В левую верхнюю
клетку нового поля, записываем значение из левой верхней клетки исходного поля – 57.
Сначала заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля,
прибавим значение из клетки , сделаем это с помощью формулы:
=A15+B1
Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.
Найдем максимальное значение суммы. Рассмотрим ячейку , в нее мы можем попасть из
и
, тогда,
чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из
которых можем попасть в эту. В ячейку
запишем формулу:
=МАКС(A16;B15)+B2
Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальной суммой, которую может собрать робот.
Для минимальной суммы порядок действий аналогичный, только формула в будет выглядеть так:
=МИН(A16;B15)+B2
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз – в соседнюю нижнюю. При попытке пересечь границы Робот разрушается Перед
каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив
клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков – сначала максимальную сумму, затем минимальную.
Нам дано поле 15 на 15, создадим рядом еще одно поле такого же размера (ячейки ) . В левую верхнюю
клетку нового поля, записываем значение из левой верхней клетки исходного поля – 73.
Сначала заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля,
прибавим значение из клетки , сделаем это с помощью формулы:
=A17+B1
Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.
Найдем максимальное значение суммы. Рассмотрим ячейку , в нее мы можем попасть из
и
, тогда,
чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из
которых можем попасть в эту. В ячейку
запишем формулу:
=МАКС(A18;B17)+B2
Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальной суммой, которую может собрать робот.
Для минимальной суммы порядок действий аналогичный, только формула в будет выглядеть так:
=МИН(A18;B17)+B2
Ошибка.
Попробуйте повторить позже
Дан квадрат клеток, в каждой клетке которого записано целое число. В левом нижнем углу квадрата
стоит Робот. За один ход Робот может переместиться на одну клетку вправо, вверх или по диагонали вправо
вверх. Выходить за пределы квадрата робот не может. Определите максимальную и минимальную сумму
чисел в клетках, которую может собрать Робот (включая начальную и конечную клетки), пройдя из левой
нижней клетки в правую верхнюю. В ответе укажите одно число – сумму максимальной и минимальной
сумм.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
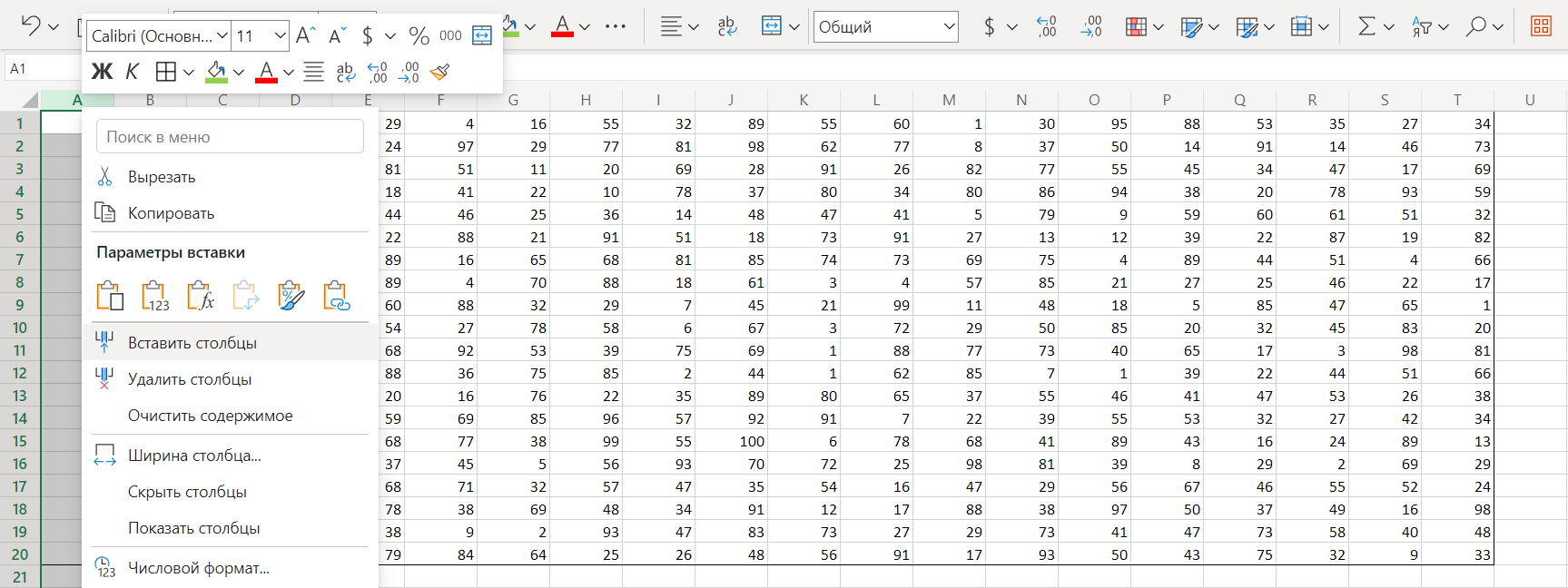
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой нижней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(B41;B42;C42)+C19
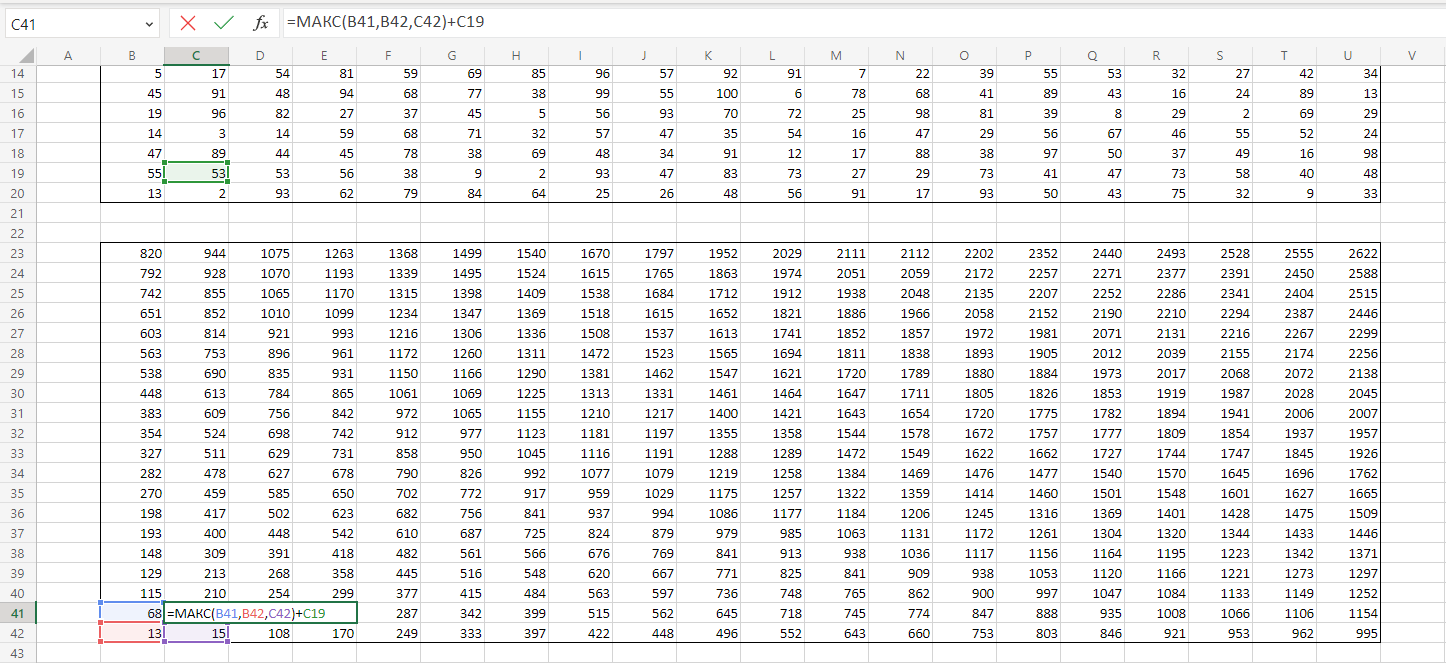
Копируем её на всю таблицу. Выписываем из правой нижней ячейки. Заменим все МИН на МАКС.
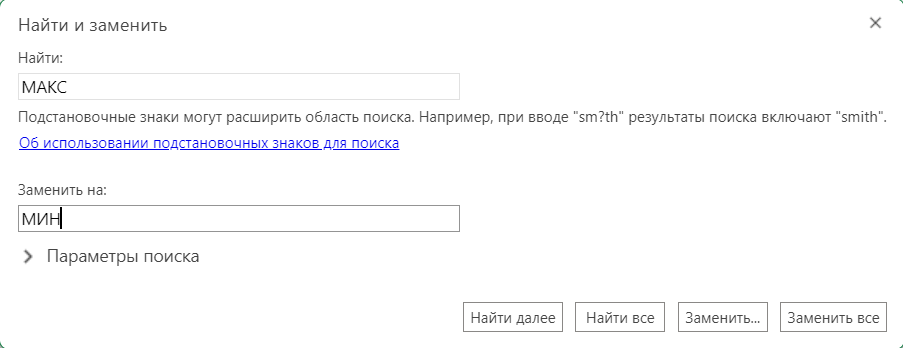
Запишем в ответ сумму двух полученных значений: +
=
.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл 18_1.xlsx. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную.
Так как робот идет из левой нижней в правую верхнюю клетку, то переписываем нижнюю левую ячейку без измнений в ячейку А22. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к изначальному значению ячейки предыдущее. В ячейку А21 пишем: =A22 + A9 и растягиваем до ячейки А13. В ячейку В22 пишем: =A22 + В10 и растягиваем до ячейки J22.
Затем в ячейке В21 пишем следующую формулу: =В9+МАКС(А21;В22). Она выбирает максимальное значение из ячеек В22 и А21, а потом прибавляет к изначальным монеткам. Растягиваем эту формула на диапазон В21:J13. В правой верхней ячейке J13 и будет искомая максимальная сумма. Она равна 1276.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН: =В9+МИН(А21;В22). Минимальная сумма равна 671.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вниз. По команде влево Робот перемещается в соседнюю левую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл 18_2.xlsx. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из правой верхней клетки в левую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Так как робот идет из правой верхней в левую нижнюю клетку, то переписываем правую верхнюю ячейку без измнений в ячейку J12. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к изначальному значению ячейки предыдущее. В ячейку J13 пишем: =J12 + J2 и растягиваем до ячейки J21. В ячейку I12 пишем: =J12 + I1 и растягиваем до ячейки A1.
Затем в ячейке I13 пишем следующую формулу: =I2+МАКС(I12;J13). Она выбирает максимальное значение из ячеек I12 и J13, а потом прибавляет к изначальным монеткам. Растягиваем эту формула на диапазон I13:A21. В левой нижней ячейке А21 и будет искомая максимальная сумма. Она равна 1181.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН: =I2+МИН(I12;J13). Минимальная сумма равна 604.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N×N клеток (1 < N < 17). В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо вниз. Выходить за пределы квадрата робот не может. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
Исходные данные записаны в файле 18_10.xlsx в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата. В ответ запишите два числа друг за другом без пробелов и разделителей — сначала максимальную сумму, затем минимальную.
Так как робот идет из левой верхней в правую нижнюю клетку, то переписываем верхнюю левую ячейку без измнений в ячейку А12. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к изначальному значению ячейки предыдущее. В ячейку А13 пишем: =A12 + A2 и растягиваем до ячейки А21. В ячейку В12 пишем: =A12 + В1 и растягиваем до ячейки J12.
Затем в ячейке В13 пишем следующую формулу: =В2+МАКС(А13;В12;A12). Она выбирает максимальное значение из ячеек A13, В12 и А12, а потом прибавляет к изначальным монеткам. Растягиваем эту формулу на диапазон В13:J21. В правой нижней ячейке J21 и будет искомая максимальная сумма. Она равна 1418.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН: =В2+МИН(А13;В12;A12). Минимальная сумма равна 531.
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную.
Так как робот идет из левой нижней в правую верхнюю клетку, то переписываем нижнюю левую ячейку без измнений в ячейку А22. Затем прописываем формулу для первой строки и для первого столбца. Мы прибавляем к изначальному значению ячейки предыдущее. В ячейку А21 пишем: =A22 + A9 и растягиваем до ячейки А13. В ячейку В22 пишем: =A22 + В10 и растягиваем до ячейки J22.
Затем в ячейке В21 пишем следующую формулу: =В9+МАКС(А21;В22). Она выбирает максимальное значение из ячеек В22 и А21, а потом прибавляет к изначальным монеткам. Растягиваем эту формула на диапазон В21:J13. В правой верхней ячейке J13 и будет искомая максимальная сумма. Она равна 1211.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН: =В9+МИН(А21;В22). Минимальная сумма равна 651.




