18.02 Робот-сборщик – условия
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на клеток (1 < N < 17). Исполнитель Робот может двигаться только вниз и вправо. Робот
может брать монеты только с тех клеток, где количество монет чётно. Если количество монет нечётно, то Робот не
берёт в этой клетке ни одной монеты. Определите максимальную и минимальную денежную сумму, которую может
собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
Исходные данные записаны в файле в виде электронной таблице размером N×N, каждая ячейка которой соответствует клетке квадрата. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную.
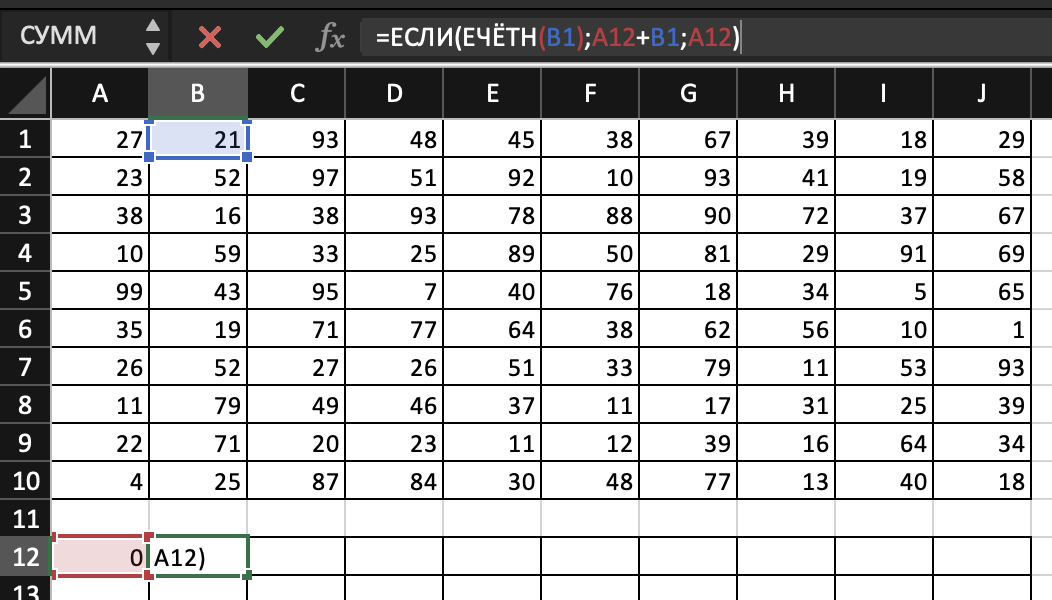
Открываем файл с таблицей. Чуть ниже основной таблицы начинаем создавать свою, в которой будем производить все вычисления. Так как робот идет из верхней левой в правую нижнюю клетку и при этом верхняя левая клетка нечетная (то есть Робот не собирает монеты в ней), то пишем 0 в начальную ячейку. Затем прописываем формулу для первой строки и для первого столбца. С помощью функции ЕЧЕТН(число), которая возрващает ИСТИНА, если число четно, и ЛОЖЬ, если число нечетно, сделаем такую проверку: если число четное, то мы прибавляем только предыдущую ячейку, а если нечетное, то предыдущую ячейку + исходную ячейку. Формула для строки выгляит так:
=ЕСЛИ(ЕЧЁТН(B1);A12+B1;A12).
Для столбца аналогично. Растягиваем формулу на всю строку и на весь столбец.
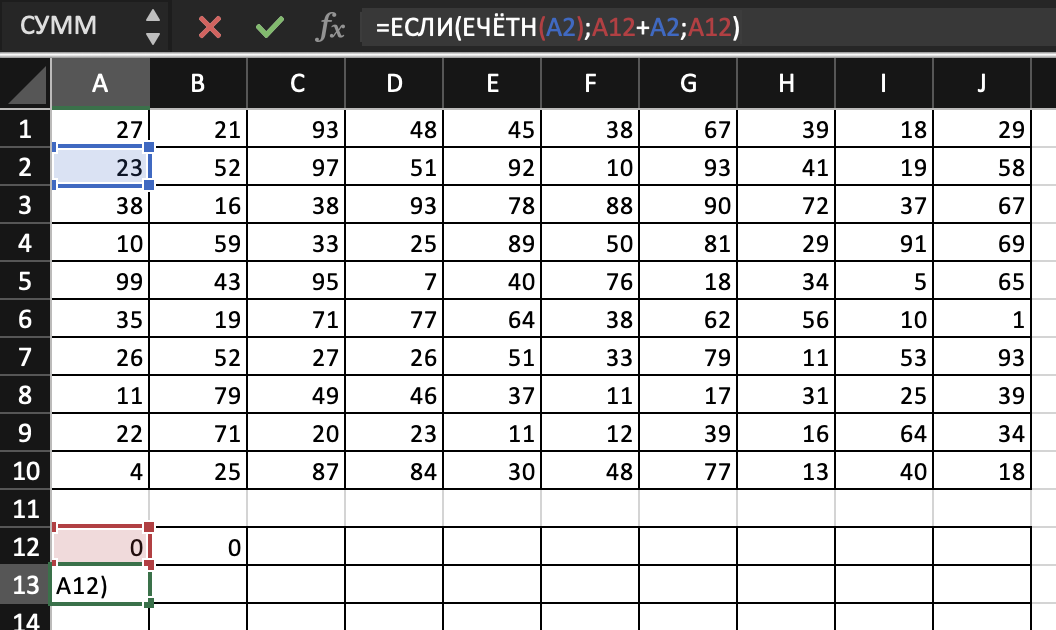
Затем в ячейке В13 пишем следующую формулу:
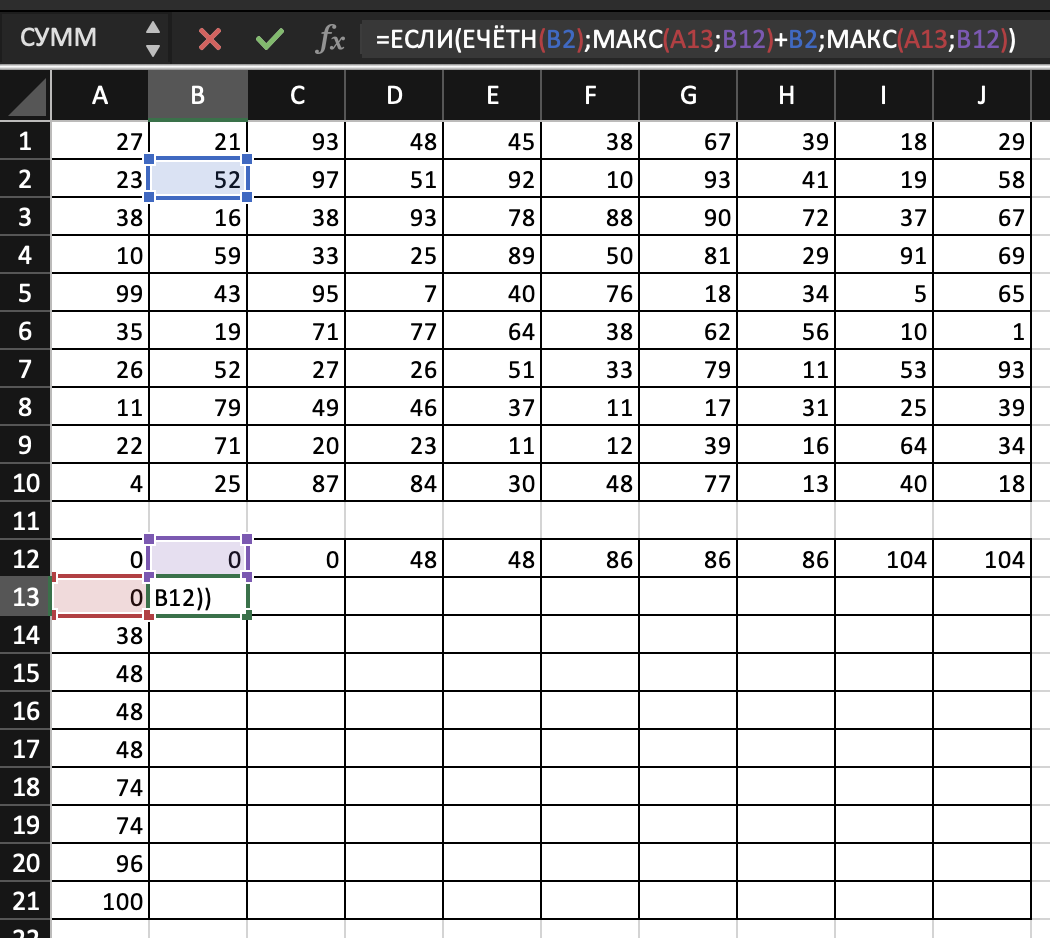
=ЕСЛИ(ЕЧЁТН(B2);МАКС(A13;B12)+B2;МАКС(A13;B12)).
То есть если в ячейке В2 нечетно количество монет, то выбирается максимальное значение из ячеек В12 и А13, а если
количество монет четно, то выбирается максимальное значение из ячеек В12 и А13 и прибавляется к изначальным
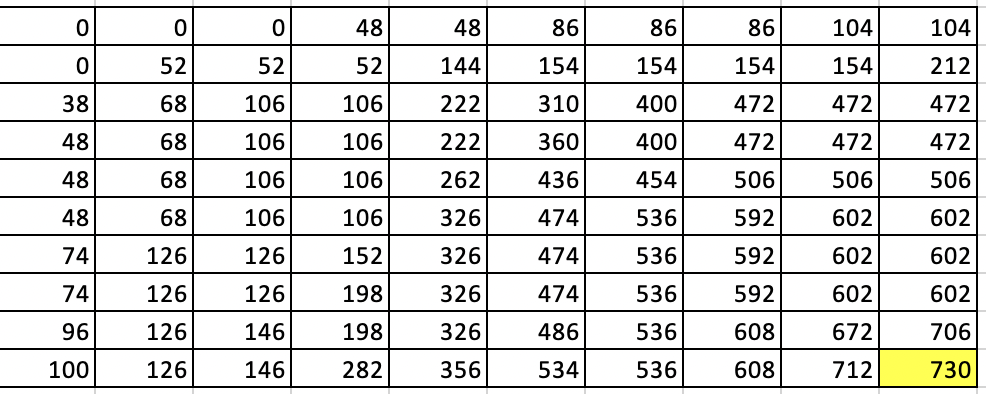
монеткам. Растягиваем эту формулу на диапазон В13:J21. В правой нижней ячейке J21 и будет искомая максимальная
сумма. Она равна 730.
Чтобы найти минимальную сумму, достаточно изменить в формуле функцию МАКС на МИН:
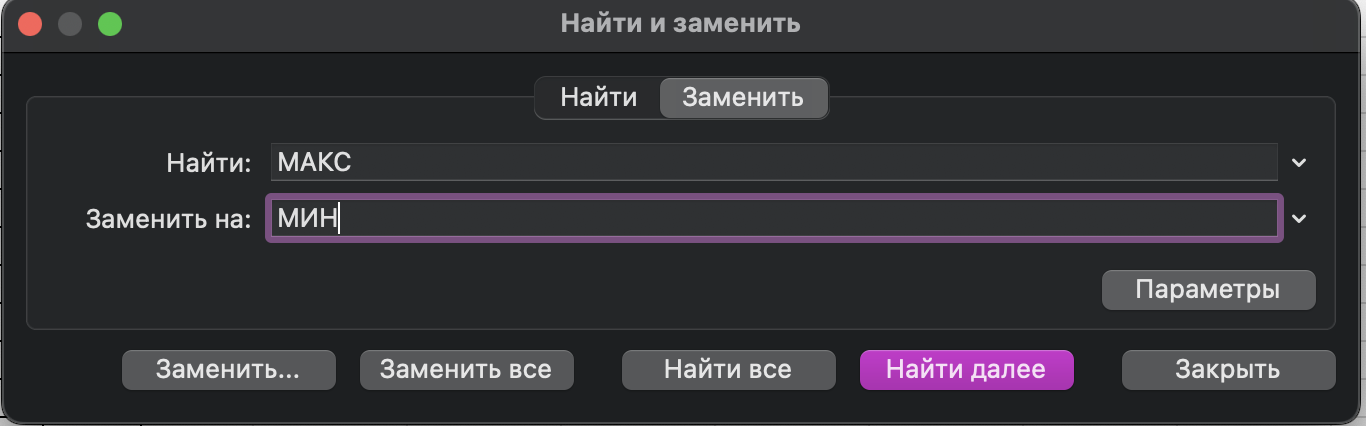
Минимальная сумма равна 78.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





