1.01 Длина кратчайшего пути между пунктами (только таблица)
Ошибка.
Попробуйте повторить позже
Между населёнными пунктами A, B, C, D, E, F, G построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
| A | B | C | D | E | F | G | |
| A | 6 | 4 | 21 | ||||
| B | 6 | 1 | |||||
| C | 4 | 1 | 5 | 27 | |||
| D | 5 | 4 | 8 | 10 | |||
| E | 4 | 1 | 8 | ||||
| F | 8 | 1 | 2 | ||||
| G | 21 | 27 | 10 | 8 | 2 | ||
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
Для удобства представим таблицу в виде графа.
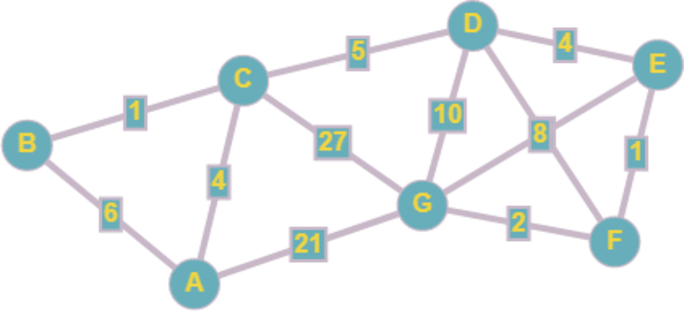
Начнем из пункта А. Из него мы можем попасть в B, С и сразу в G. Запомним, что A-G = 21. Пункт В приведет только к пункту С. A-B-C = 6 + 1 = 7, A-C = 4. Т.к. в обоих случаях мы попадаем в пункт С, выбираем наиболее короткий путь: это прямой путь A-C = 4.
Из пункта C мы можем попасть в пункт D и в пункт G – нашу цель. До пункта C длина пути 4, из С в G – 27, то есть A-G = 31. Это больше, чем прямой путь, посчитанный ранее, поэтому это значение запоминать не будем.
Значит, идем в пункт D. A-D = A-C + 5 = 9. Из пункта D можем попасть в E, F.
Посмотрим, какой маршрут короче. Из пункта F мы можем попасть в E – и оттуда в G – и сразу в G. D-F-E-G = 8 + 1 + 8 = 17, D-F-G = 8 + 2 = 10. Из пункта E можем пойти в F – и потом в G – или сразу в G: D-E-F-G = 4 + 1 + 2 = 7, D-E-G = 4 + 8 = 12. Выбираем кратчайший маршрут: D-E-F-G = 7.
Итак, A-C = 4, D-E-F-G = 7, то есть A-G = 4 + 5 + 7 (учитываем дорогу C-D) = 16. Прямая дорога A-G = 21, а A-C-D-E-F-G = 16.
Значит, ответ – 16.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




