18.06 Прочие прототипы
Ошибка.
Попробуйте повторить позже
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную денежную сумму, которую может собрать Робот, при условии что робот не
может делать больше одинаковых команд подряд, а так же длину этого пути. В ответ запишите два числа друг за
другом без разделительных знаков — сначала максимальную сумму, затем длину пути.
Исходные данные представляют собой электронную таблицу размером , каждая ячейка которой соответствует
клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
Суть решения будет заключаться в том, что мы будем контролировать, чтобы два хода не повторялись, через запоминание предыдущих:
Создадим у новой таблицы границы и с помощью специальной вставки (CTRL + C CTRL + ALT + V
форматы) создадим 4 новые таблицы, которые назовём как на картинке:
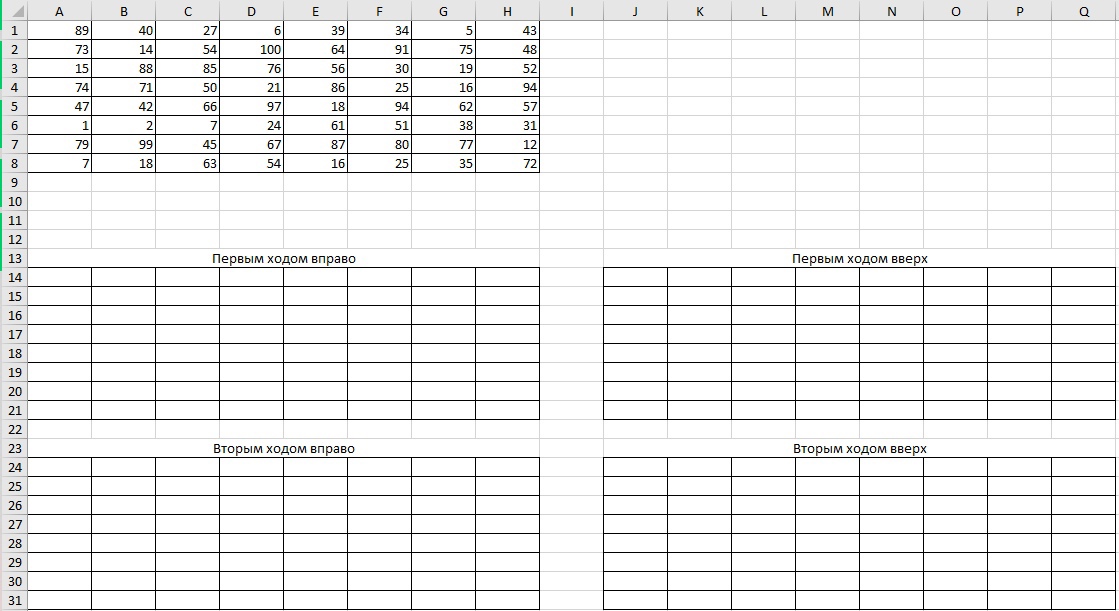
Заполним -10000 ячейки, в которые нельзя попасть их ходами:

Для ячейки B21 пишем формулу =A8+B8, так как это будет первый ход вправо из начальной. Для ячейки J20 пишем формулу =A8+A7, так как это будет первый ход вверх из начальной. Нижние таблицы можем заполнить формулами, в которых будем складывать предыдущее значение из верхней для неё таблицы и текущее значение из основной таблицы, то есть для C31 это формула =B21+C8 и можем этой формулой заполнить всю таблицу. Для правой нижней таблицы то же самое, то есть для ячейки J29 это формула =J20+A6.
Получаем такое:
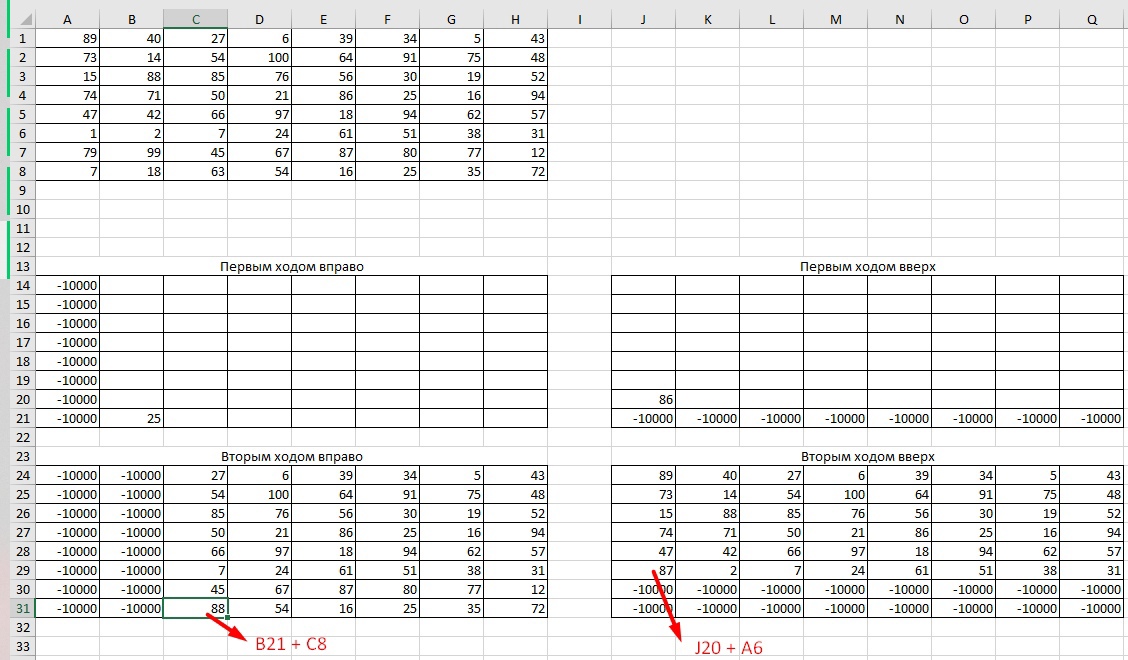
Так как в ячейки, следующие за первым ходом, нельзя попасть повторным ходом, их тоже заполняем -100000
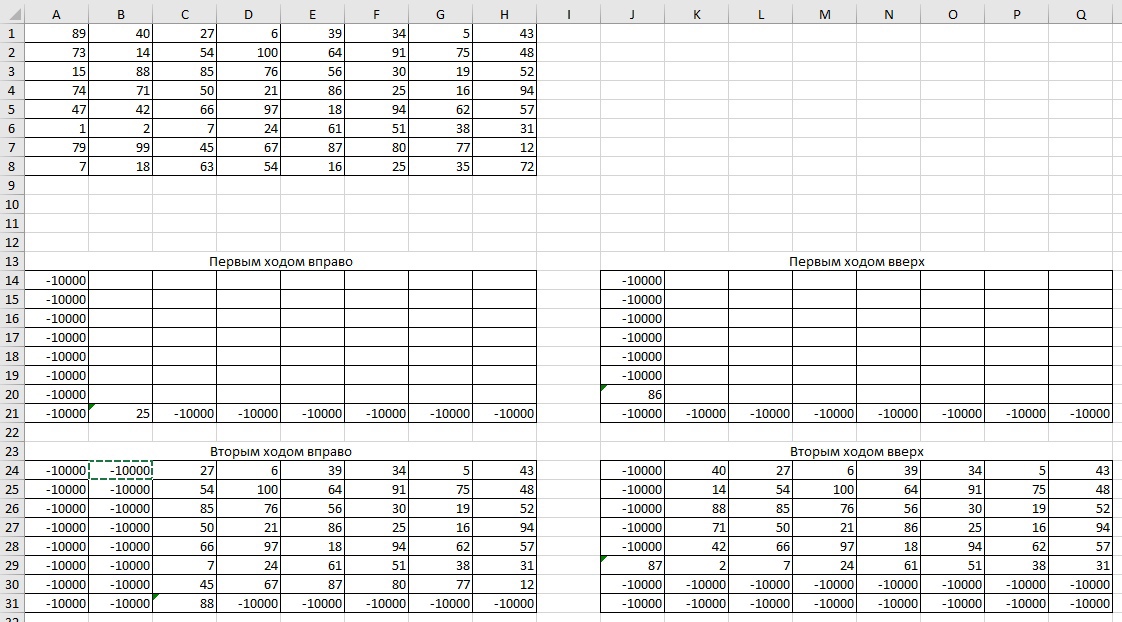
Теперь можем заполнить только конечные формулы и распространить их на оставшиеся ячейки. Для конечной ячейки в таблице первым ходом право: мы можем в неё попасть из предыдущей ячейки таблицы первым ходом вверх и предыдущей ячейки таблицы первым ходом вверх, получается формула: =МАКС(P14;P24)+H1. Такой же логикой заполняем для таблицы первым ходом вверх: =МАКС(H15;H25)+H1. Распространяем обе формулы и получаем:
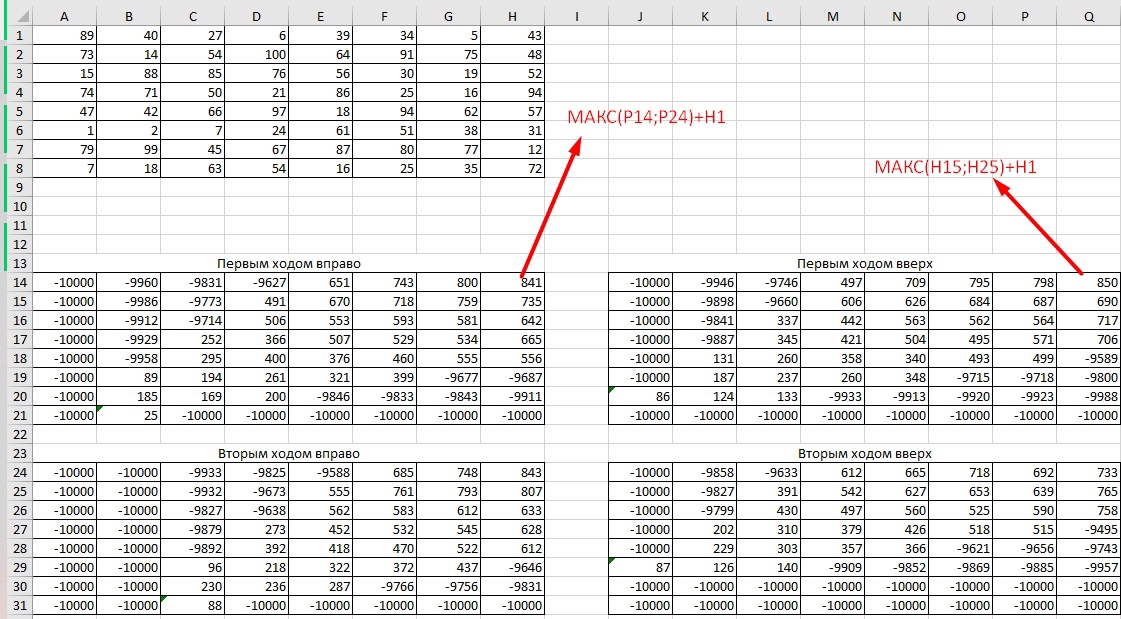
Находим максимум из 4 таблиц - это и есть ответ - 850.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





