Прочие прототипы —Каталог задач по ЕГЭ - Информатика БУ

Ошибка.
Попробуйте повторить позже

Задача 1#22898

Задание выполняется с использованием прилагаемых файлов

Дан квадрат $N × N$ клеток $(1 < N < 20)$ . В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы квадрата робот не может. При этом ведётся подсчёт суммы по следующим правилам: число в очередной клетке, через которую проходит робот, включается в сумму, если оно меньше числа в предыдущей клетке на пути робота. Если число в очередной клетке не меньше числа в предыдущей, сумма не изменяется. Число в начальной клетке всегда включается в сумму. Необходимо переместить робота в правый нижний угол так, чтобы полученная сумма была максимальной.

В ответе запишите максимально возможную сумму.

Вложения к задаче

Задание 18.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

Выделяем всю таблицу и добавляем границы.

$PIC$

Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B18$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C18$ записываем формулу =МАКС(ЕСЛИ(C2<B2;C2+B18;B18);ЕСЛИ(C2<C1;C2+C17;C17))

$PIC$

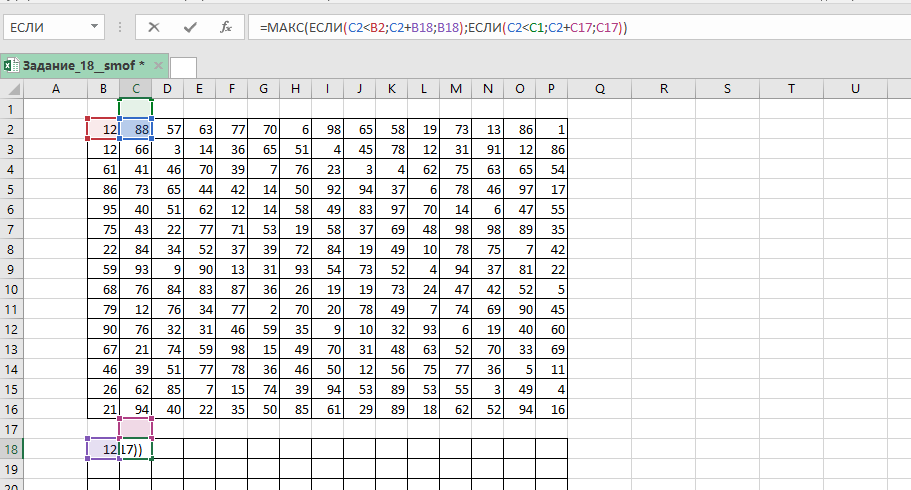
Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки в ответ.

Ответ: 876

Ошибка.
Попробуйте повторить позже

Задача 2#25964

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на $N × N$ клеток $(1 < N < 30)$ . Крабу нужно перейти через пляж со стороны джунглей (верхняя строка) в сторону океана (нижняя строка). Он может начать переход с любой клетки верхней строки и закончить на любой клетке нижней строки. Краб за одно перемещение может попасть в одну из трех клеток следующей строки: на клетку вниз или на одну из клеток слева/справа от нижней. При попытке сходить влево или вправо (без смены строки), назад (в предыдущую строку) или за границы поля Краба съедают. На пляже могут быть песчаные ловушки (помечены красным). При попадании в ловушку Краб становится чьим-то ужином. В каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Краб забирает монету с собой; это также относится к начальной и конечной клетке маршрута Краба.

Определите максимальную денежную сумму, которую может собрать Краб, пройдя со стороны джунглей (сверху) до океана (снизу).

Вложения к задаче

Задание 18.xlsx

Показать ответ и решение

Так как нам ни в коем случае нельзя проходить через красные клетки, то в исходной таблице заменим их на -1 000 000.

$PIC$

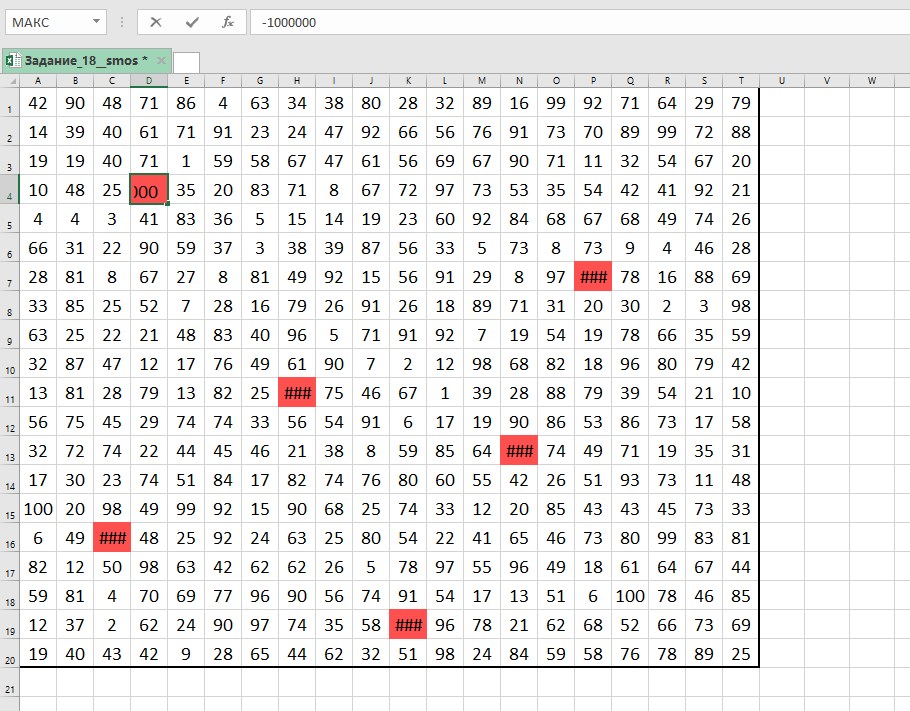
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В первую строку полученной таблицы копируем первую строку исходной таблицы. Слева добавим столбец, чтобы не пришлось менять формулу для некоторых ячеек (нажимаем правой кнопкой мыши на столбец $A$ и выбираем «Вставить»).

$PIC$

В ячейку $B24$ записываем формулу =МАКС $(A23;B23;C23 )+ B2$ .

$PIC$

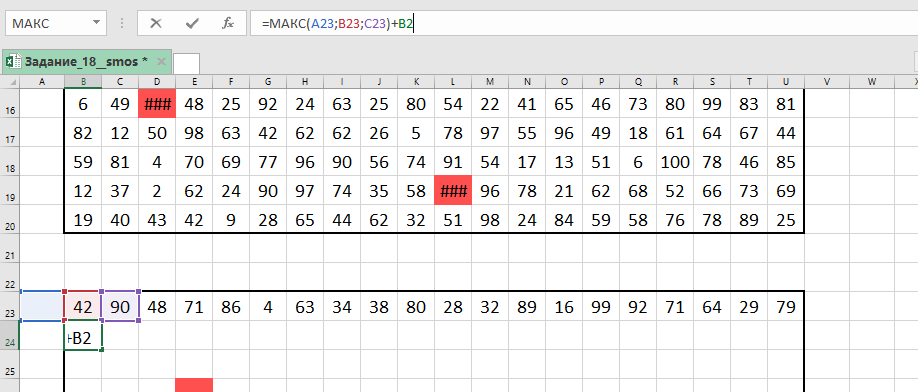
Копируем её на все ячейки таблицы.
Находим максимум из всех значений в последней строке и запишем ответ.

$PIC$

Ответ: 1643

Ошибка.
Попробуйте повторить позже

Задача 3#25991

Задание выполняется с использованием прилагаемых файлов

Дан квадрат $N × N$ клеток $(1 < N < 20)$ . Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке пересечь границы квадрата, обозначенные жирными линиями, Робот умирает. В каждой клетке квадрата указан её тип латинскими буквами $A$ , $B$ или $C$ . Посетив клетку, Робот платит или получает деньги за её посещение; это также относится к начальной и конечной точке маршрута. За посещение клетки $A$ взимается плата $10$ монет, за посещение клетки $B$ Роботу выплачивают $2$ монеты, за посещение клетки $C$ Роботу выплачивают $3$ монеты. Определите минимальное и максимальное количество монет, которое может получить Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа через пробел — сначала наименьшее число монет, затем наибольшее.

Вложения к задаче

Задание_18__g57r.xlsx

Показать ответ и решение

С помощью найти и заменить заменяем все A на -10, B на 2, C на 3.

$PIC$

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

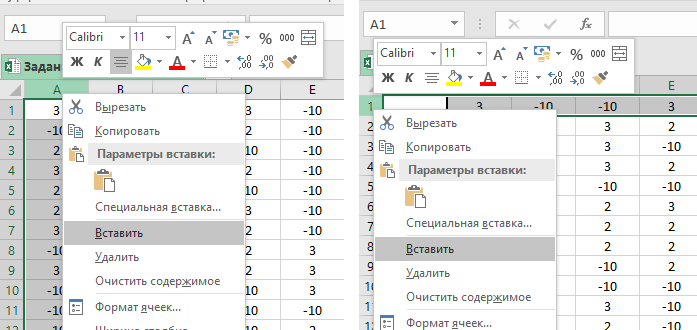
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B21$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C21$ записываем формулу =МАКС(C20;B21)+C2.

$PIC$

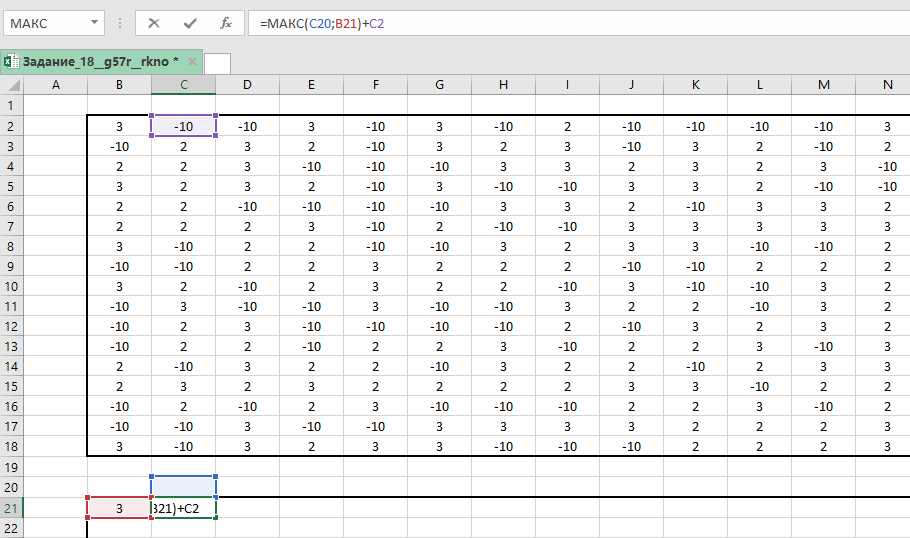
Копируем формулу на все оставшиеся клетки и выписываем значение из правой нижней ячейки.
Заменим все МАКС на МИН и также выпишем значение из правой нижней клетки.

$PIC$

Запишем в ответ сначала минимальный результат, затем через пробел - максимальный.

Ответ: -184 51

Ошибка.
Попробуйте повторить позже

Задача 4#26070

Квадрат разлинован на $N × N$ клеток $(1 < N < 30).$ Исполнитель № $456$ попал в «Игру в кальмара», чтобы ему выбраться, придется пройти $3$ уровня игры. На первом уровне у № $456$ есть зеленые зоны, через которые ему обязательно нужно пройти, иначе № $456$ умирает и теряет шанс выбраться из игры. На втором уровне у № $456$ есть красные зоны, при попадании в которые он умирает и теряет шанс выбраться из игры. На третьем уровне у № $456$ появляются стены, через которые он не может пройти, при попытке пересечь стену № $456$ умирает и теряет шанс выбраться из игры. В каждой клетке квадрата есть монета достоинством от $1$ до $100$ . Определите максимальное количество монет, которое может собрать № $456$ , пройдя «Игру в кальмара». В ответе укажите одно число — наибольшее количество монет (сумму максимального количества монет на трёх уровнях).

1 Уровень: из левой верхней клетки попасть в правую нижнюю клетку, обязательно проходя через зеленые клетки, с помощью команд: вниз на одну клетку, вправо на одну клетку.

2 Уровень: из левой нижней клетки попасть в правую верхнюю клетку, не проходя через красные клетки, с помощью команд: вверх на одну клетку, вправо на одну клетку.

3 Уровень: из правой нижней клетки попасть в левую верхнюю клетку, не проходя через стены, с помощью команд: влево на одну клетку, вверх на одну клетку.

Исходные данные представляют собой электронную таблицу с $3$ -мя листами, где каждый лист — отдельный уровень, в котором содержится квадрат размером $N × N$ , каждая ячейка которого соответствует количеству монет в клетке квадрата.

Пример входных данных:

$PIC$

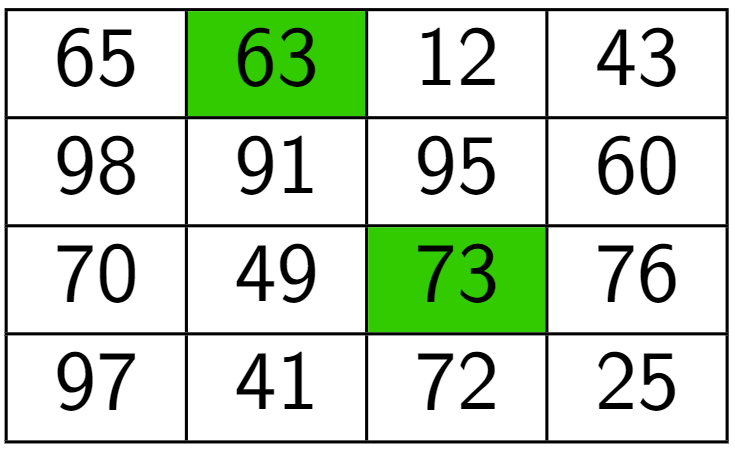
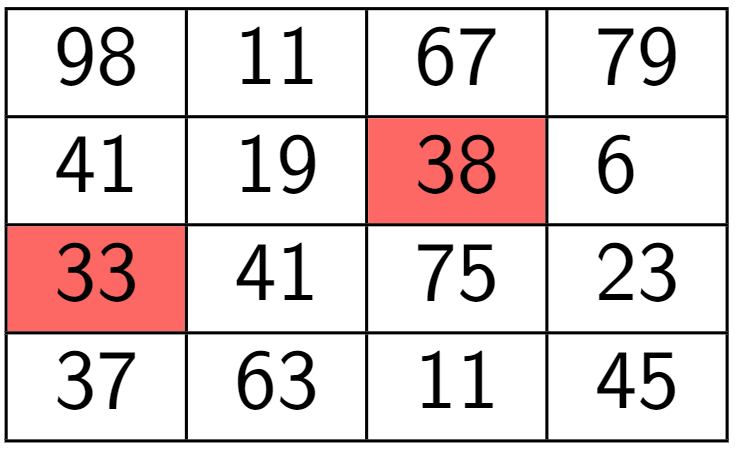
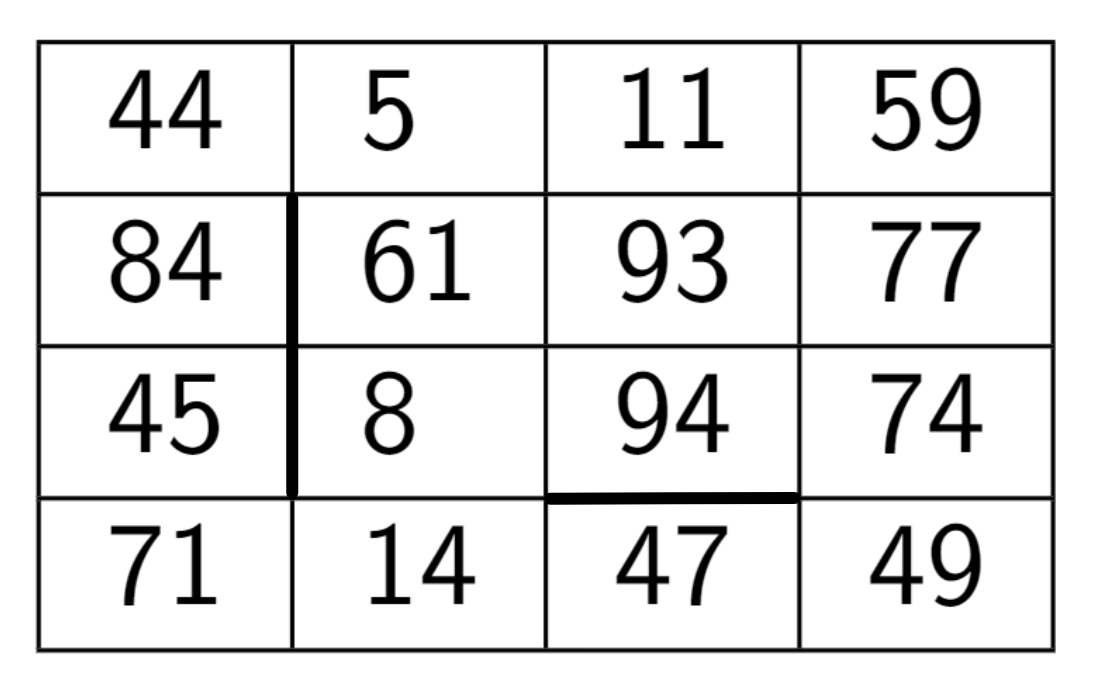
Для указанных входных данных ответом будет сумма трёх чисел $488 + 324 + 420 = 1232$ .

Вложения к задаче

Задание_18__gmt3.xlsx

Показать ответ и решение

1 Уровень.
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
Так как нам обязательно нужно пройти через зелёные клетки, то в исходной таблице добавим в каждую по 1 000 000.

$PIC$

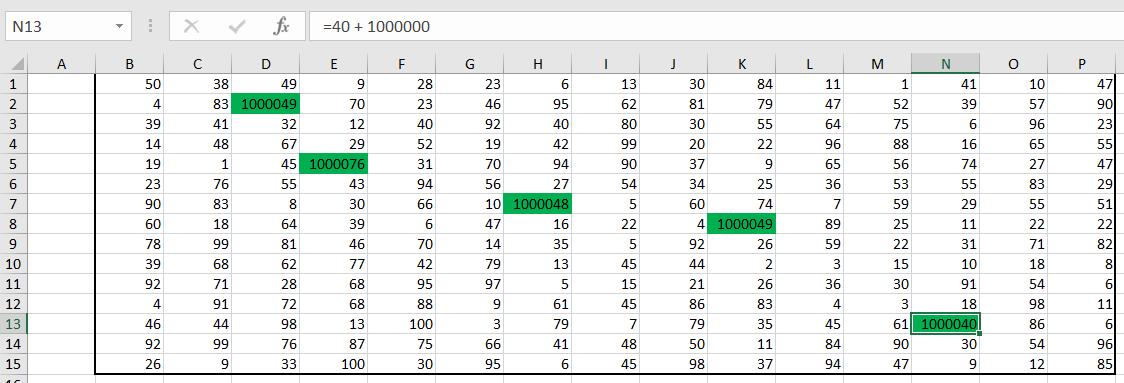
В начало маршрута (в нашем случае $A19$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $B19$ записываем формулу = $A19 + B1$ и копируем её на всю строку. В ячейку $A20$ записываем формулу = $A19 + A2$ и копируем её на всю строку. В $B20$ записываем =МАКС $(B19;A20 )+ B2$ и вставляем эту формулу во все оствшиеся клетки таблицы.

$PIC$

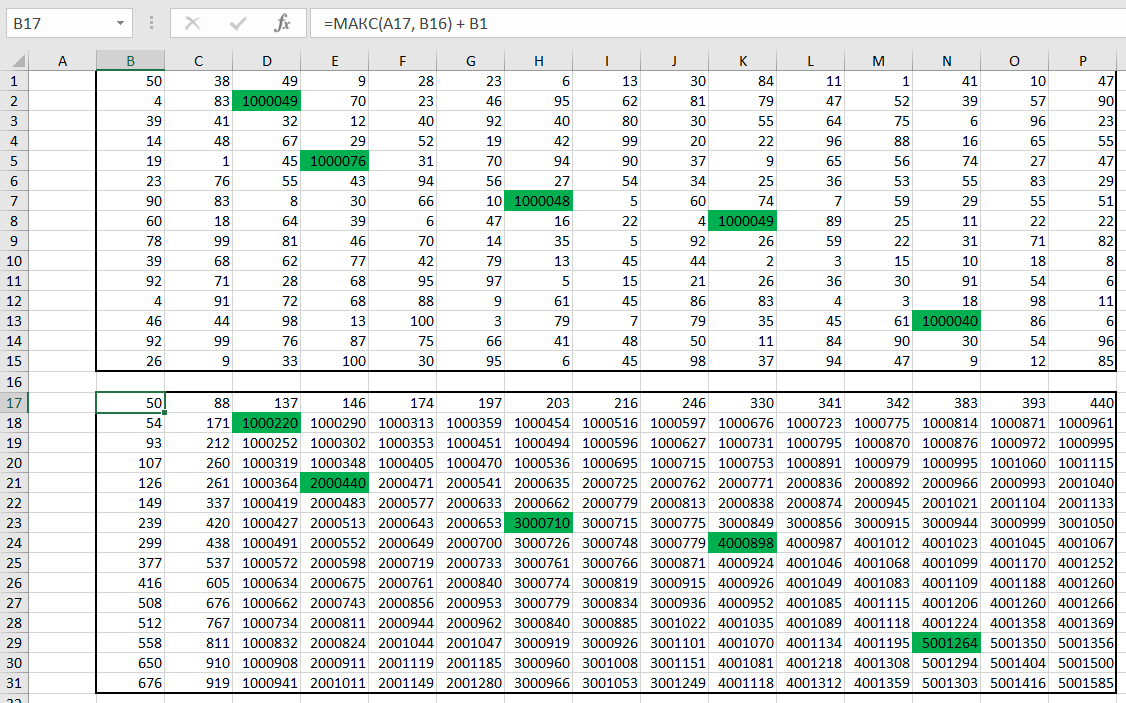
На данном уровне мы нашли максимальное количество монет, которое можем собрать, соблюдая все условия, но не забываем, что мы специально добавили несколько миллионов.
Так как у нас $5$ зеленых клеток, то запишем в любую свободную ячейку формулу = $O33 − 5000000$

$PIC$

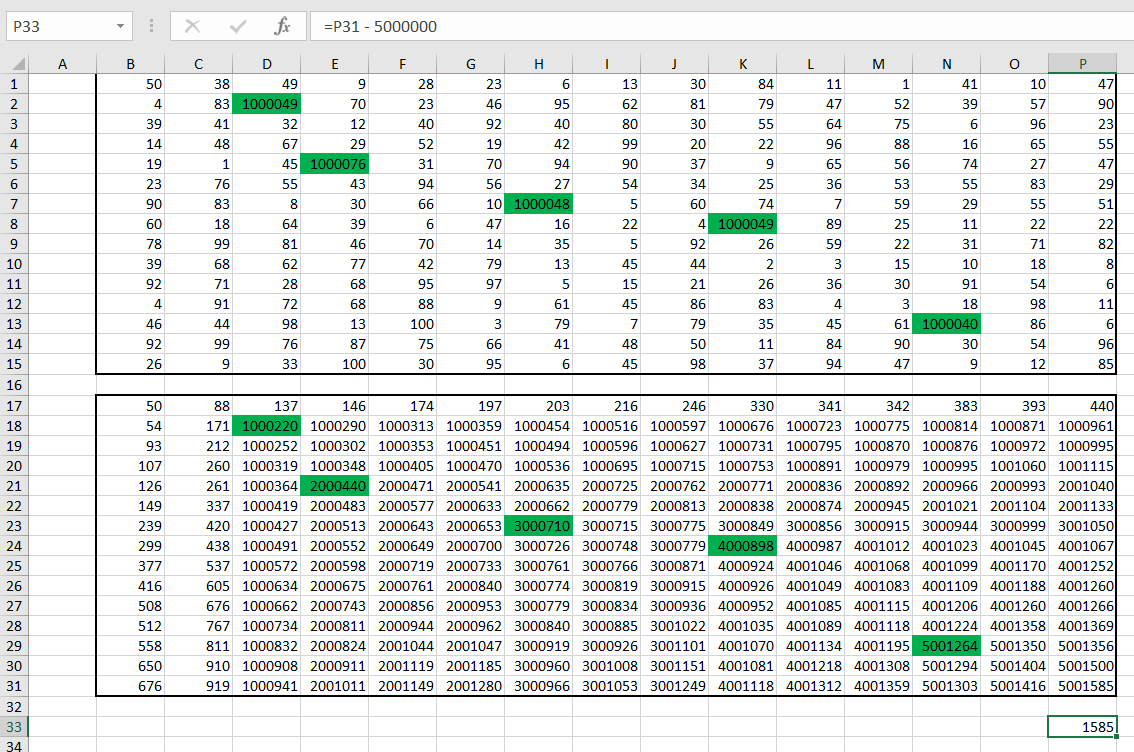
Теперь у нас есть ответ для данного уровня, перейдём к следующему.

2 Уровень.
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
Так как нам ни в коем случае нельзя проходить через красные клетки, то в исходной таблице заменим их на -1 000 000.

$PIC$

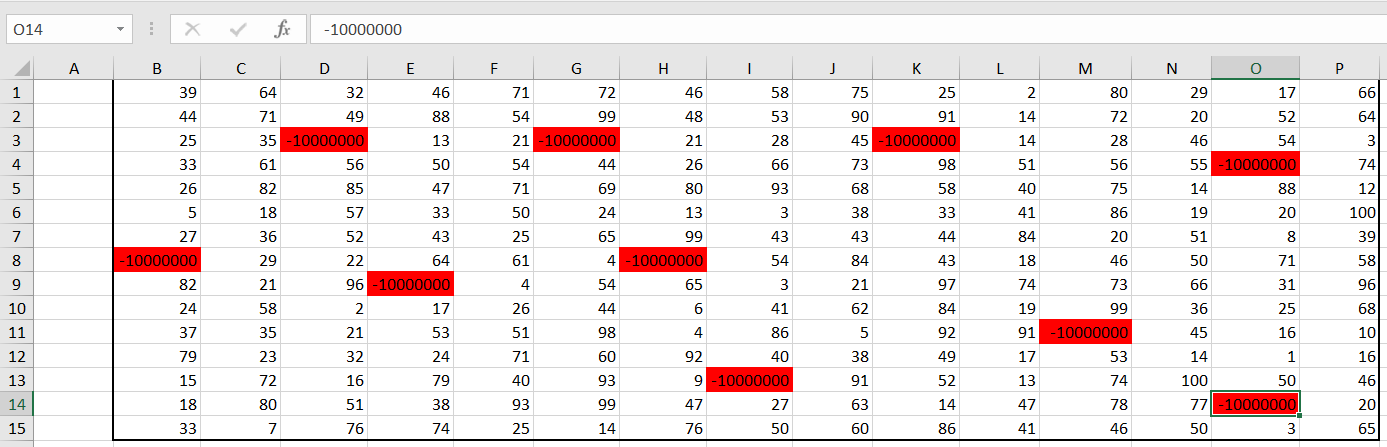
В начало маршрута (в нашем случае $A33$ ) записываем значение левой нижней клетки данной нам таблицы. В клетку $B33$ записываем формулу = $A33 + B15$ и копируем её на всю строку. В ячейку $A32$ записываем формулу = $A33 + A14$ и копируем её на всю строку. В $B32$ записываем =МАКС $(B33;A32) +B14$ и вставляем эту формулу во все оствшиеся клетки таблицы.

$PIC$

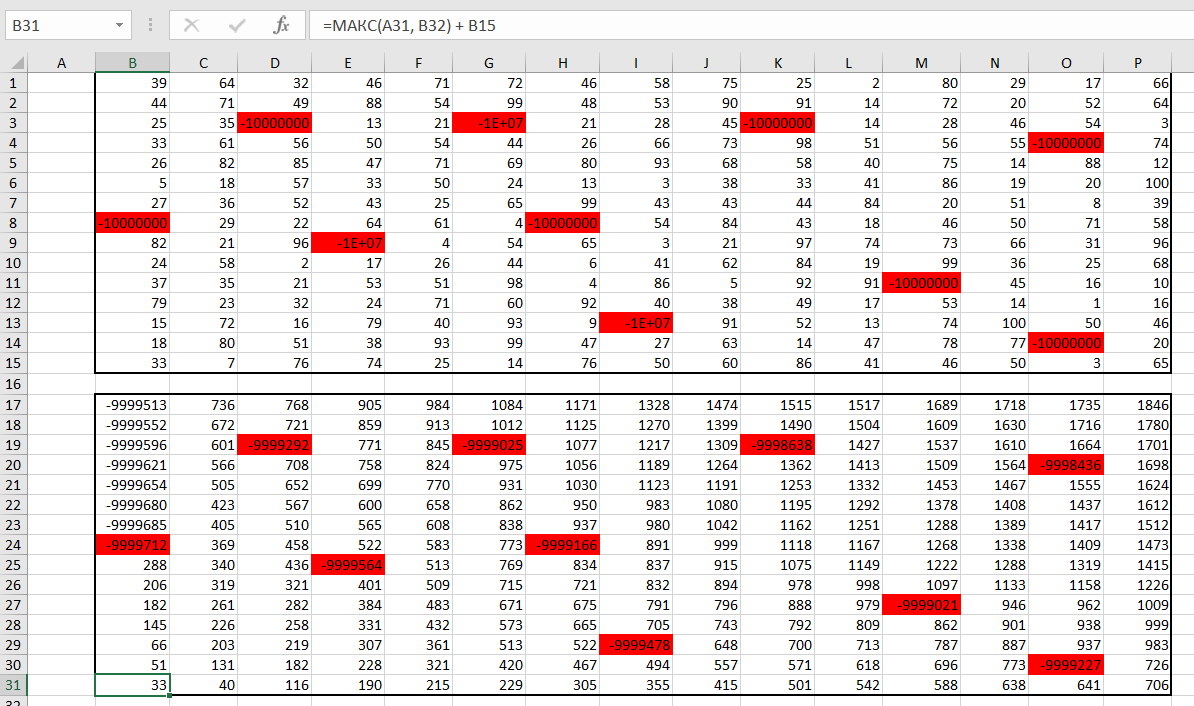
На данном уровне мы нашли максимальное количество монет (ячейка $O19$ ), которые можем собрать, соблюдая все условия, перейдём к следующему.

3 Уровень.
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (ячейка $O33$ ) скопируем значение из ячейки $O15$ . В $O32$ запишем формулу =МАКС $(P32;O33 )+ O14$ и заполним ей все оставшиеся ячейки таблицы.

$PIC$

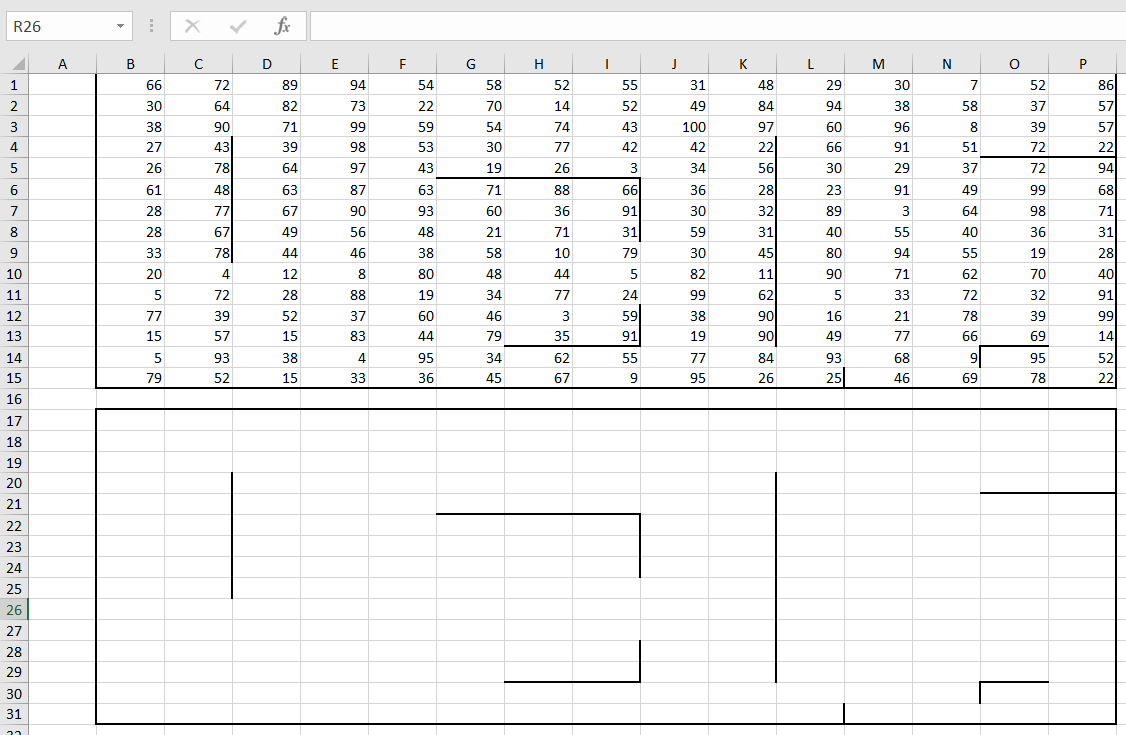
Теперь изменим формулы там, где у нас находятся границы.
Если границы мешают нам пройти выше, то меняем формулы в клетках, находящихся под границами, то есть убираем из них значение ячейки идущей выше границы.

$PIC$

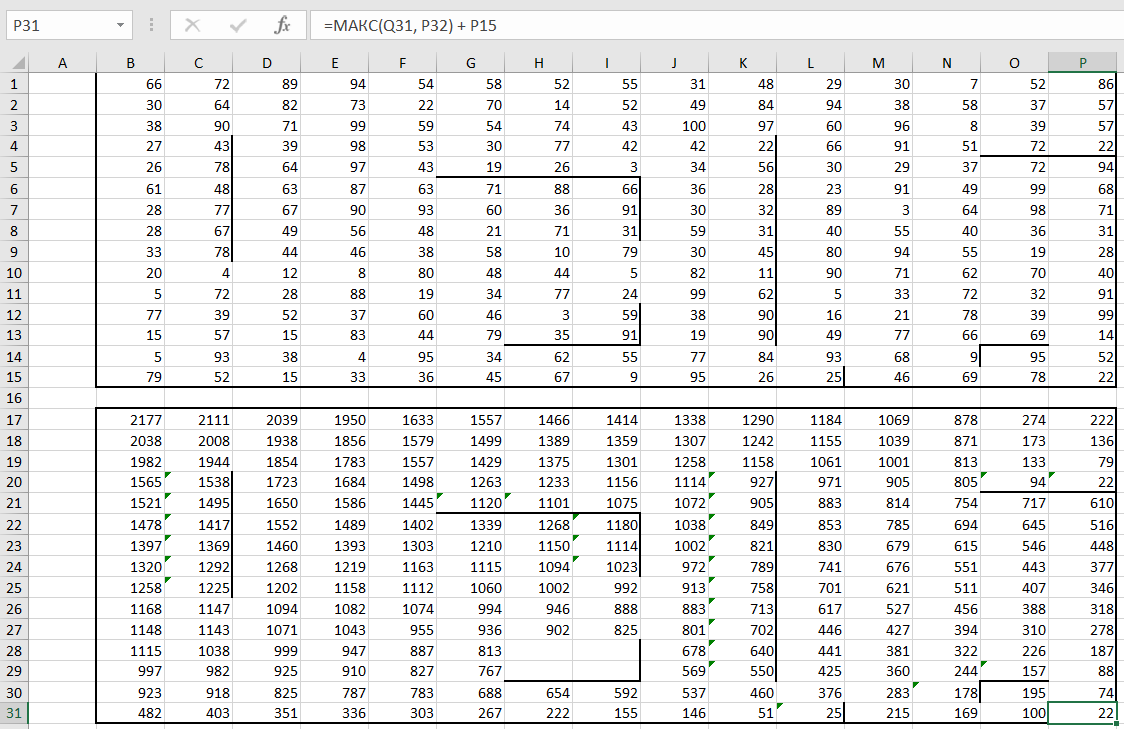
Если граница мешает нам идти влево, то убираем из текущей формулы значение ячейки, идущей после границы.

$PIC$

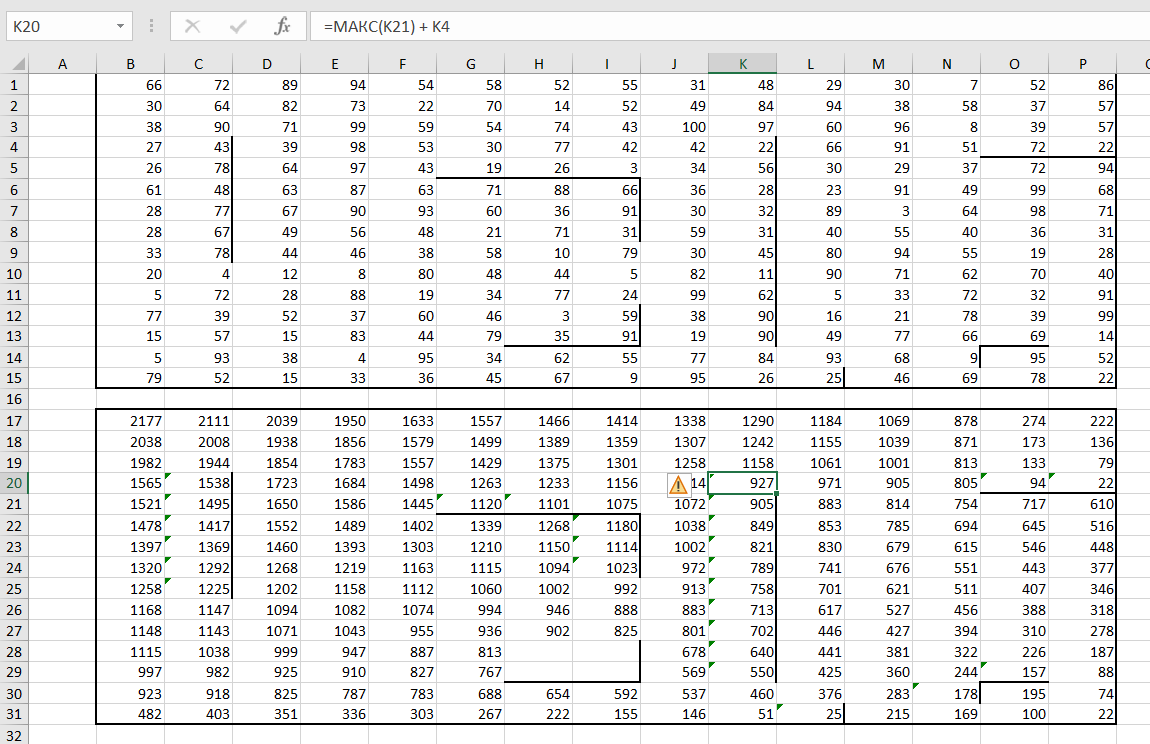
В клетке $A19$ ответ для текущего уровня.

Суммируем все три полученных числа и получаем итоговый ответ.

Ответ: 5608

Ошибка.
Попробуйте повторить позже

Задача 5#26124

Роботу нужно перейти через поле с верхней строки на нижнюю строку. Он может начать переход с любой клетки верхней строки и закончить на любой клетке нижней строки. С каждым шагом Робот переходит в следующий ряд и может за одно перемещение попасть в одну из трех клеток следующей строки (на клетку прямо или боковые с ней). Ходы только в бок (без смены строки) и назад запрещены. В каждой клетке поля лежит монета достоинством от $1$ до $100$ . Робот собирает все монеты по пройденному маршруту. Известно, что Робот собрал максимальное количество монет, пройдя с верхней строки до нижней строки. В ответе укажите сумму количества монет из первой и последней клетки маршрута.

Вложения к задаче

Задание_18__hi6u.xlsx

Показать ответ и решение

Выделяем всю таблицу и добавляем границы.

$PIC$

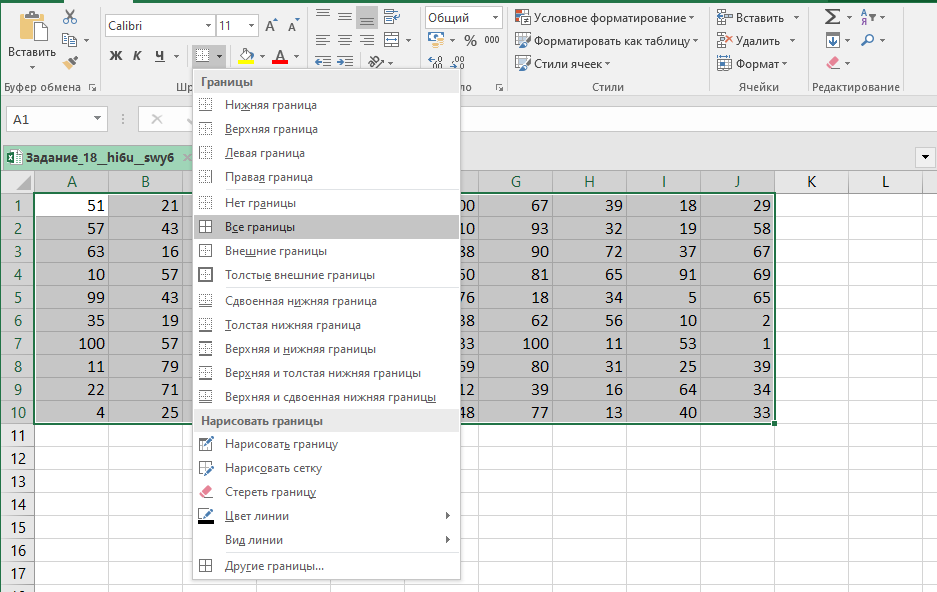
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат. В первую строку полученной таблицы копируем первую строку исходной таблицы. Слева добавим столбец, чтобы не пришлось менять формулу для некоторых ячеек (нажимаем правой кнопкой мыши на столбец $A$ и выбираем «Вставить»).

$PIC$

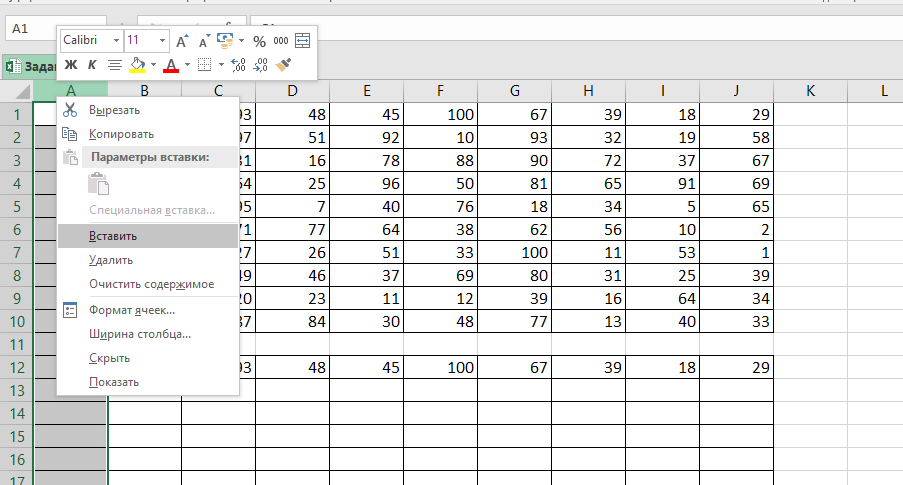
В ячейку $B13$ записываем формулу =МАКС $(A12;B12;C12 )+ B2$

$PIC$

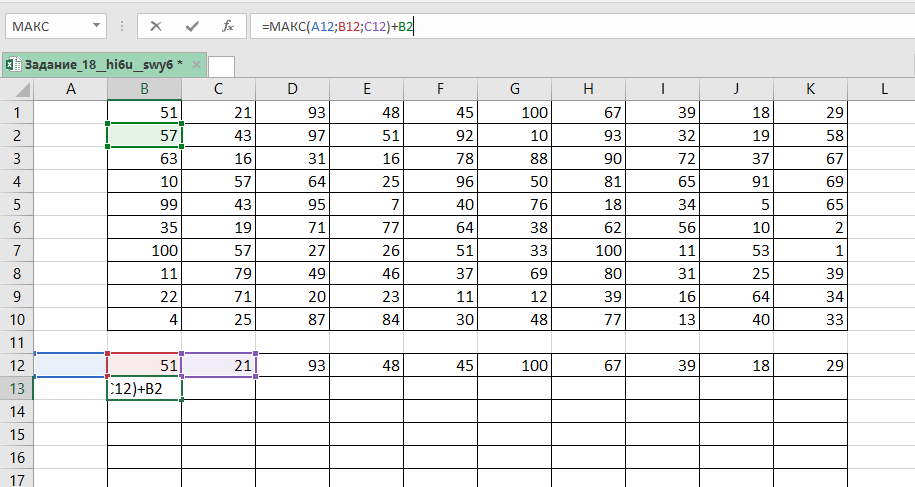
Копируем её на все ячейки таблицы.
Находим максимум из всех значений в последней строке, выпишем найденное число.

$PIC$

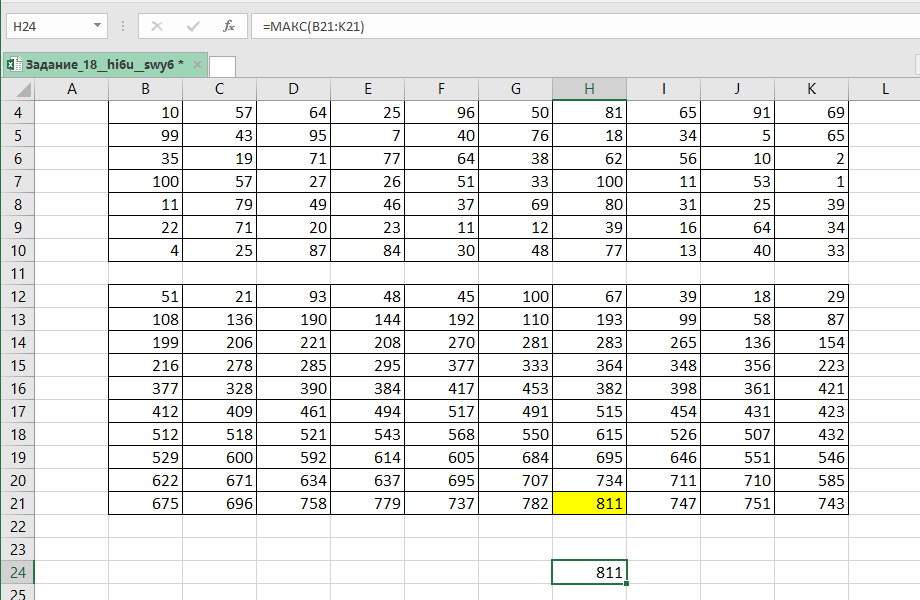
Теперь восстановим маршрут робота, начиная с этого числа, выбираем максимальное число из клеток, в которые мог заходить робот ходом ранее. Таким образом доходим до верхней строки.

$PIC$

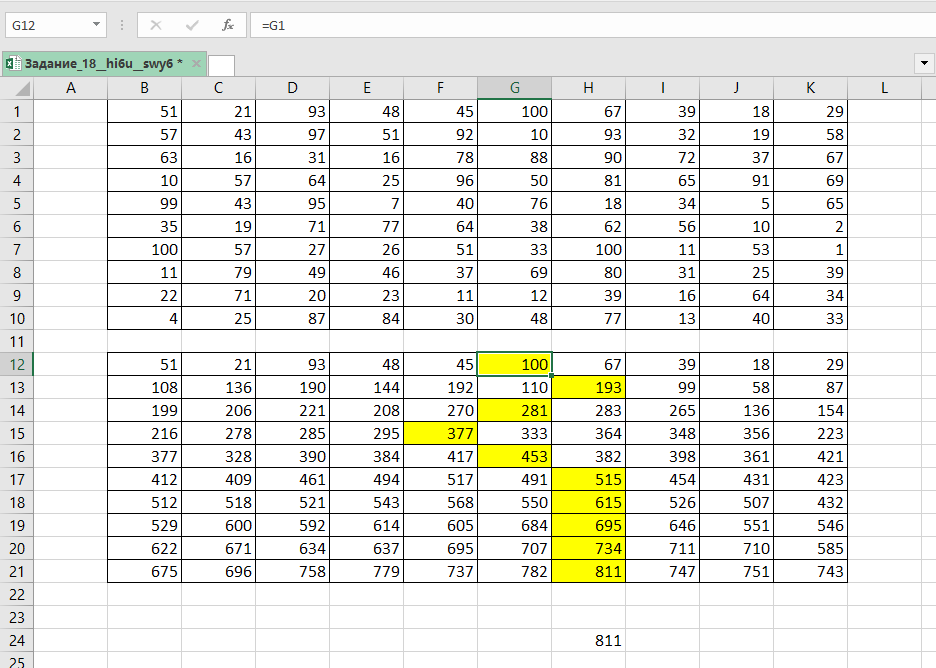
Суммируем это число с выписанным и записываем ответ.

Ответ: 911

Ошибка.
Попробуйте повторить позже

Задача 6#28000

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на $N × N$ клеток $(1 < N < 17)$ . Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную денежную сумму, которую может собрать Робот, при условии что робот не может делать больше $2$ одинаковых команд подряд, а так же длину этого пути. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем длину пути.

Исходные данные представляют собой электронную таблицу размером $N × N$ , каждая ячейка которой соответствует клетке квадрата.

Пример входных данных:

$|---|---|---|--| |-7-|9--|8--|6-| |10 |12 |2 |5 | |-1-|8--|15-|2-| |---|---|---|--| --1--6---12--8-|$

Для указанных входных данных ответом должна быть пара чисел:

$|---|--| -47--6-|$

Вложения к задаче

Задание 18.xlsx

Показать ответ и решение

Суть решения будет заключаться в том, что мы будем контролировать, чтобы два хода не повторялись, через запоминание предыдущих:

Создадим у новой таблицы границы и с помощью специальной вставки (CTRL + C $→$ CTRL + ALT + V $→$ форматы) создадим 4 новые таблицы, которые назовём как на картинке:

$PIC$

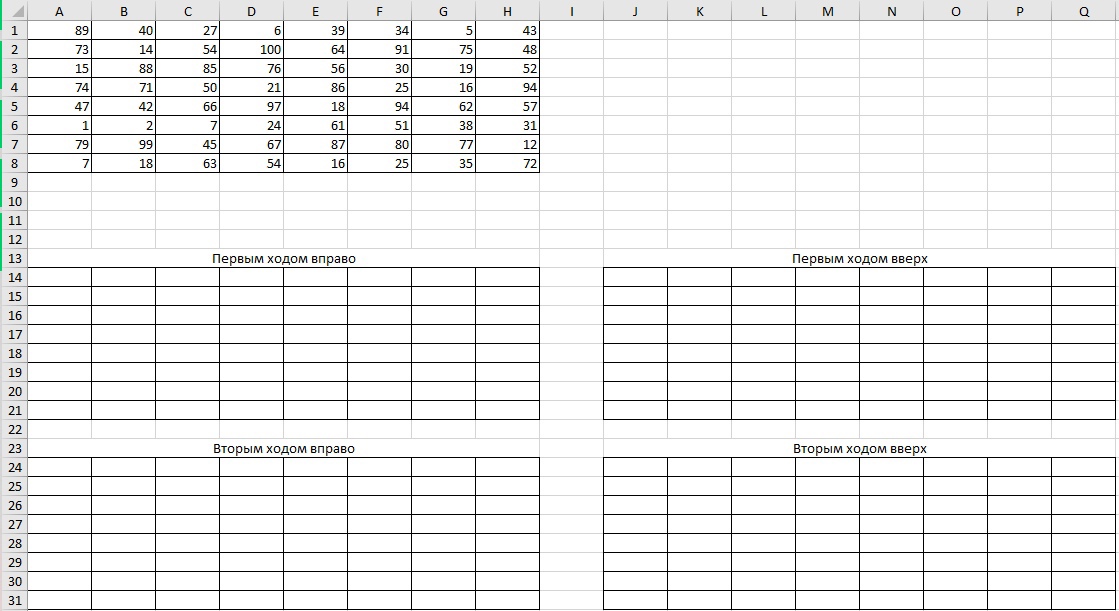
Заполним -10000 ячейки, в которые нельзя попасть их ходами:

$PIC$

Для ячейки B21 пишем формулу =A8+B8, так как это будет первый ход вправо из начальной. Для ячейки J20 пишем формулу =A8+A7, так как это будет первый ход вверх из начальной. Нижние таблицы можем заполнить формулами, в которых будем складывать предыдущее значение из верхней для неё таблицы и текущее значение из основной таблицы, то есть для C31 это формула =B21+C8 и можем этой формулой заполнить всю таблицу. Для правой нижней таблицы то же самое, то есть для ячейки J29 это формула =J20+A6.

Получаем такое:

$PIC$

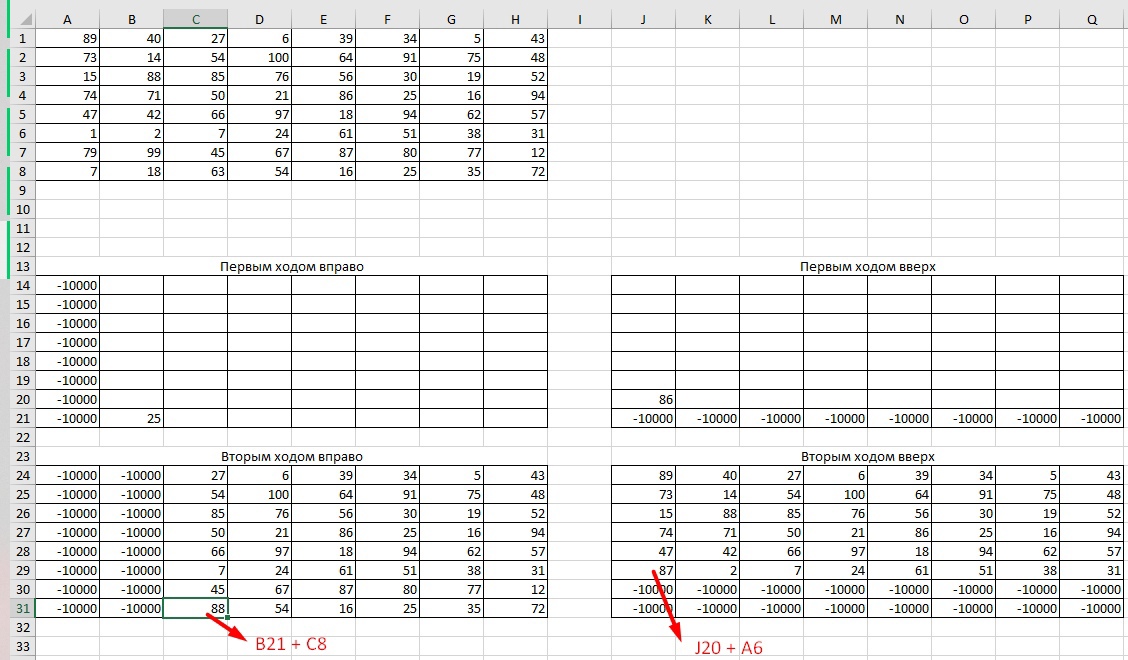
Так как в ячейки, следующие за первым ходом, нельзя попасть повторным ходом, их тоже заполняем -100000

$PIC$

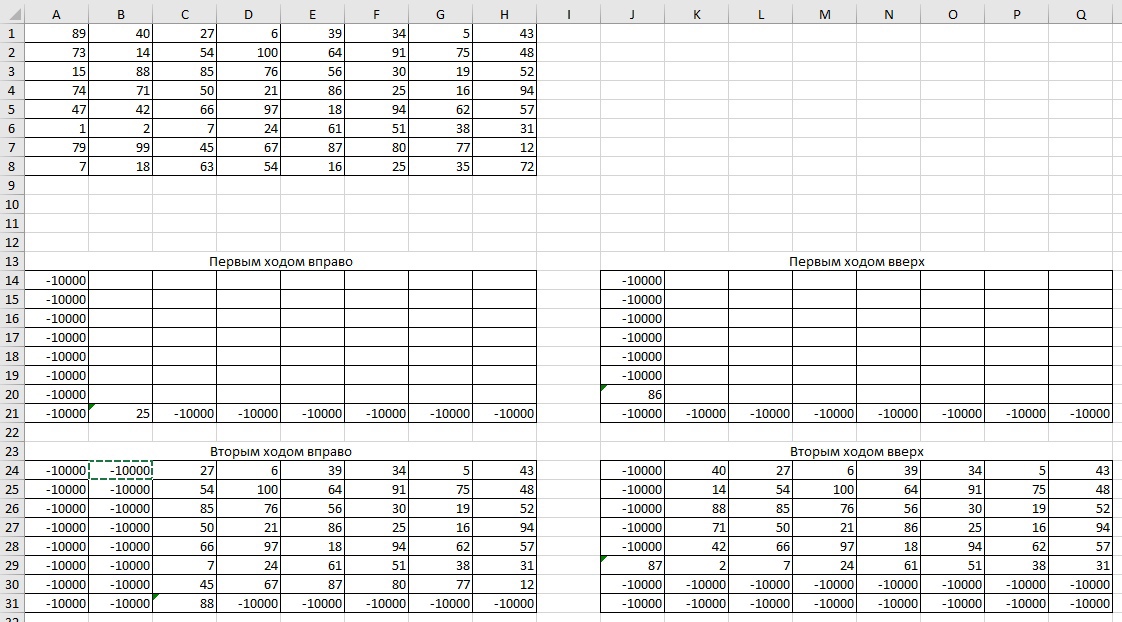
Теперь можем заполнить только конечные формулы и распространить их на оставшиеся ячейки. Для конечной ячейки в таблице первым ходом право: мы можем в неё попасть из предыдущей ячейки таблицы первым ходом вверх и предыдущей ячейки таблицы первым ходом вверх, получается формула: =МАКС(P14;P24)+H1. Такой же логикой заполняем для таблицы первым ходом вверх: =МАКС(H15;H25)+H1. Распространяем обе формулы и получаем:

$PIC$

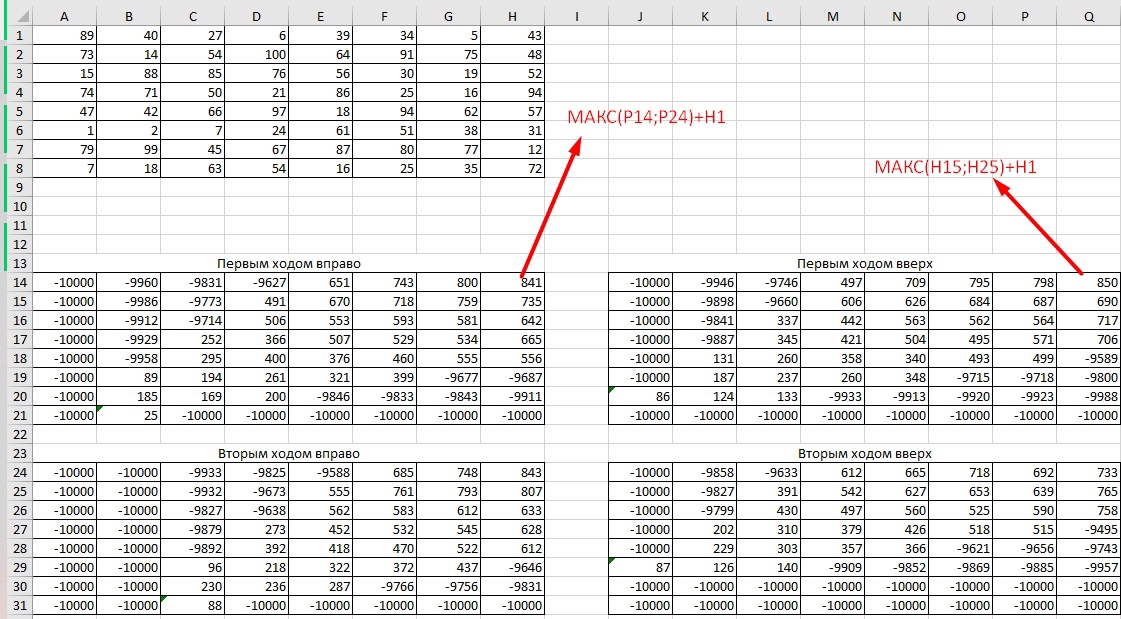
Находим максимум из 4 таблиц - это и есть ответ - 850.

Ответ: 85014

Ошибка.
Попробуйте повторить позже

Задача 7#30153

Задание выполняется с использованием прилагаемых файлов.

Квадрат разлинован на $N × N$ клеток $(1 < N < 17)$ . Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. В квадрате есть клетки, помеченные зеленым. В них сидят котики. Робот очень любит котиков и обязательно пройдет через эти клетки, чтобы погладить котиков. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную денежную сумму, которую может собрать Робот, начиная путь из верхней левой клетки. В ответ запишите одно число — максимальную сумму, которую может собрать Робот.

Исходные данные представляют собой электронную таблицу размером $N × N$ , каждая ячейка которой соответствует клетке квадрата.

Вложения к задаче

4.xlsx

Показать ответ и решение

Так как нам обязательно нужно пройти через зелёные клетки, то в исходной таблице добавим в каждую по $1000000$ .

$PIC$

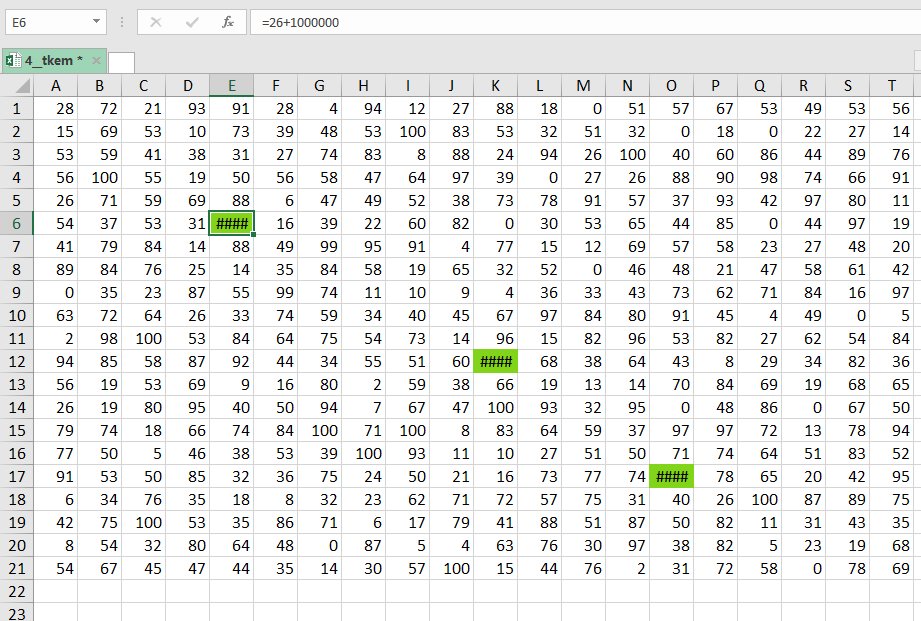
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить).

$PIC$

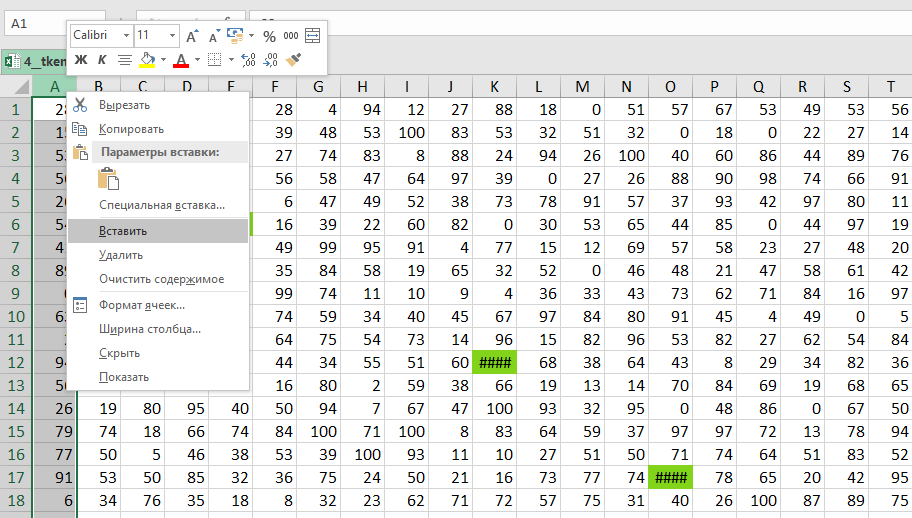
Выделяем всю таблицу и добавляем границы.

$PIC$

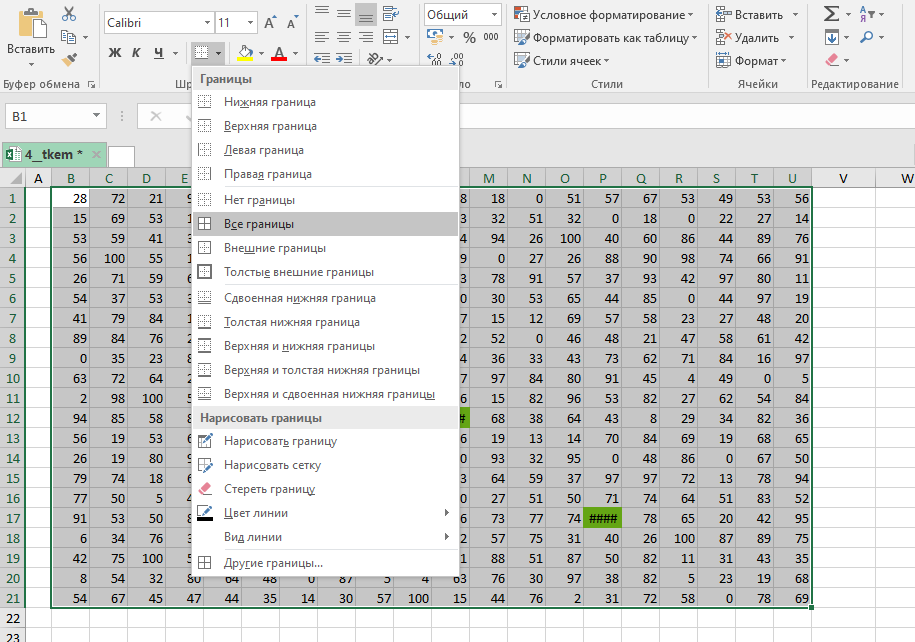
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B25$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C25$ записываем формулу =МАКС(C24;B25)+C1

$PIC$

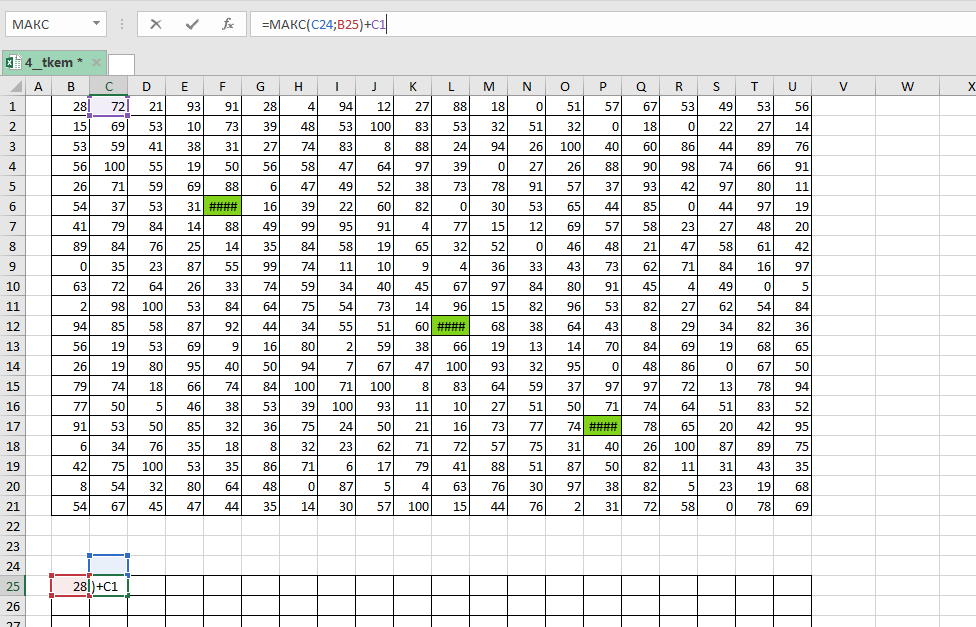
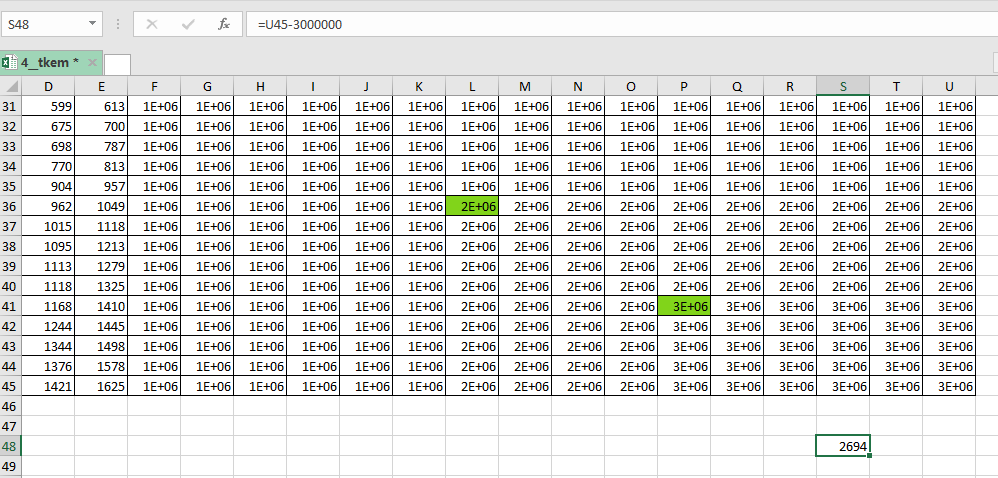
Вставляем эту формулу во все оствшиеся клетки таблицы. Не забываем, что мы специально добавили несколько миллионов. Так как у нас $3$ зеленые клетки, то запишем в любую свободную ячейку формулу =U45-3000000, полученное число и есть ответ.

$PIC$

Ответ: 2694

Ошибка.
Попробуйте повторить позже

Задача 8#30155

Задание выполняется с использованием прилагаемых файлов.

Квадрат разлинован на $N × N$ клеток $(1 < N < 20)$ . Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вверх. По команде влево Робот перемещается в соседнюю левую клетку, по команде вверх — в соседнюю верхнюю. Если робот пересекает границу поля, то он уничтожается. Каждая клетка заполнена одним из двух чисел: $0$ или $1$

Если в клетке записано число $1$ , то Робот может попасть в эту клетку

Если в клетке записано число $0$ , то Робот не может попасть в такую клетку.

Определите количество способов, которыми Робот может попасть из правой нижней клетки в левую верхнюю. В ответе укажите искомое число.

Вложения к задаче

6.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить).

$PIC$

Выделяем всю таблицу и добавляем границы.

$PIC$

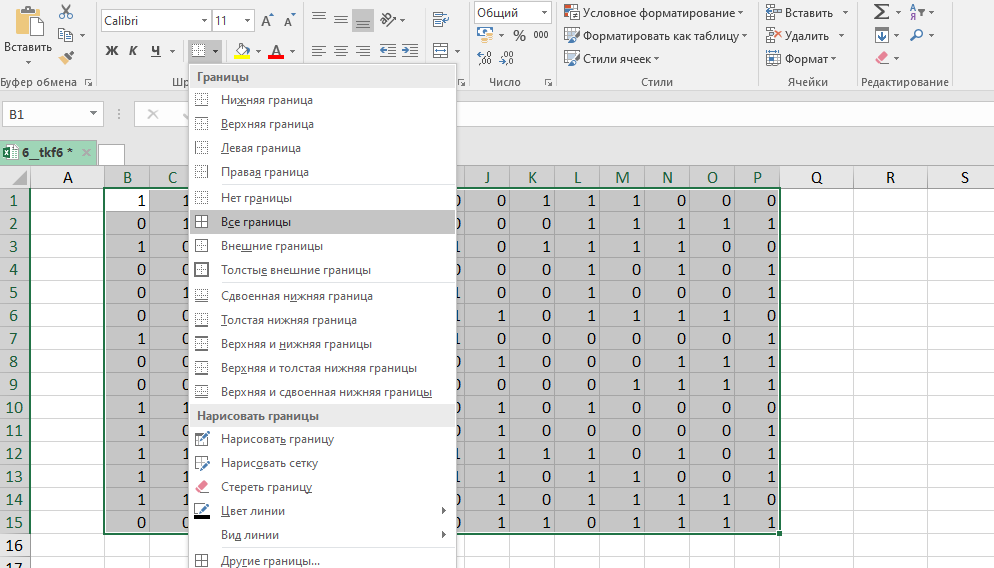
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $P 32$ ) записываем значение правой нижней клетки данной нам таблицы. В клетку $O32$ записываем формулу =ЕСЛИ(O15=0;0;O33+P32)

$PIC$

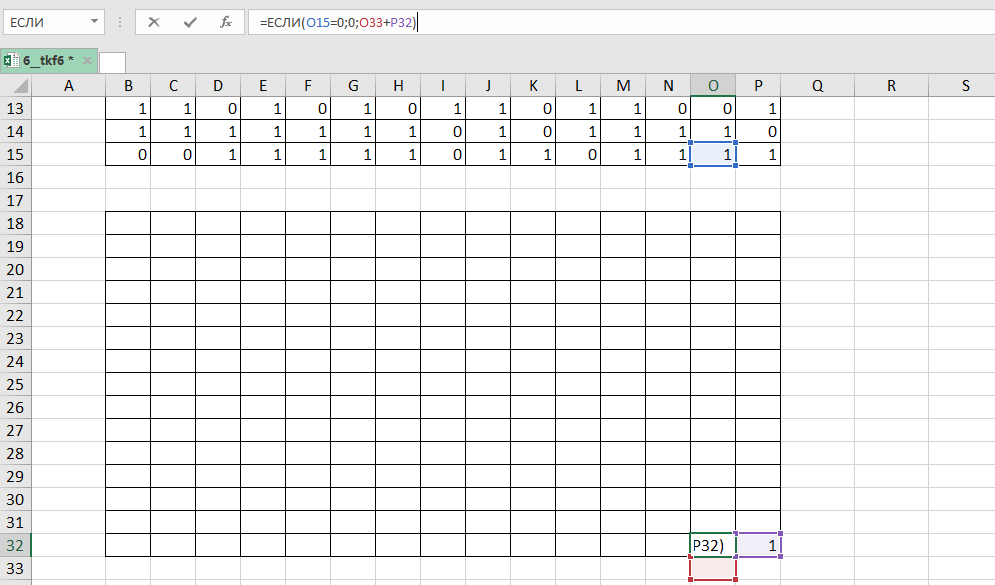
Копируем её на всю таблицу.
Полученное в левой верхней клетке значение запишем в ответ.

Ответ: 12

Ошибка.
Попробуйте повторить позже

Задача 9#30156

Квадрат разлинован на N $×$ N клеток (3 < N < 15). В каждой клетке записано целое число. На поле работает исполнитель Контур, которого можно разместить в любой клетке поля; далее он не перемещается. Контур суммирует числа во всех клетках вокруг клетки, в которой он находится. Для клеток, находящихся на краю квадрата, он находит сумму значений клеток, которые лежат внутри квадрата. Например, для ячейки А1 нужно найти сумму В1, А2, В2. Необходимо найти минимальный и максимальный результаты работы исполнителя и записать их в ответ через пробел.

Вложения к задаче

7.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

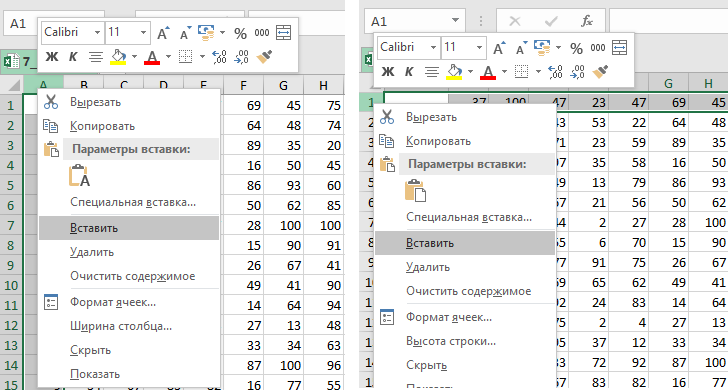
Выделяем всю таблицу и добавляем границы.

$PIC$

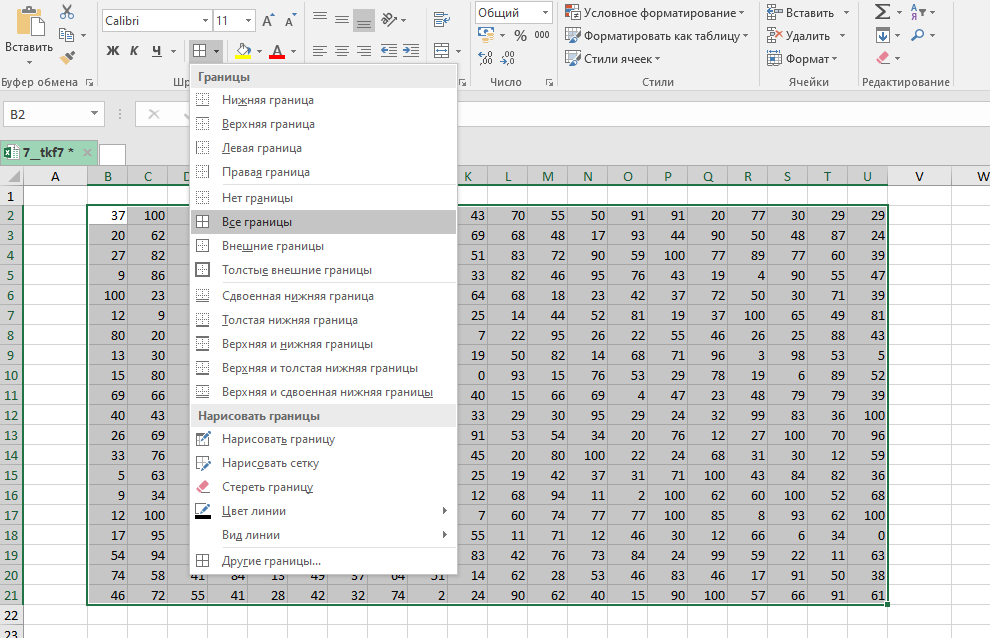
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
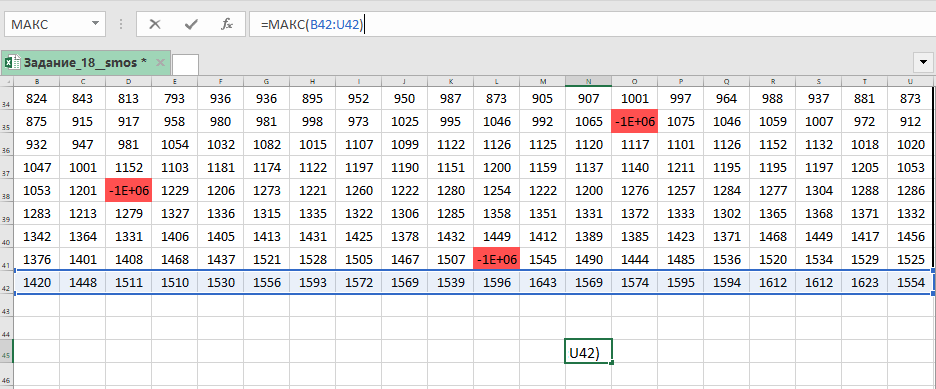
В клетку $B24$ записываем формулу =A1+B1+C1+C2+C3+B3+A3+A2 и копируем её на всю таблицу.

$PIC$

В свободной клетке запишем формулу =МАКС(B24:U43), а в другой - =МИН(B24:U43).
Запишем в ответ сначала минимальный результат, затем через пробел - максимальный.

Ответ: 84 669

Ошибка.
Попробуйте повторить позже

Задача 10#30159

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на N $×$ N клеток (1 < N < 25). Исполнитель Пассажир на Самокатике перемещается из левой верхней клетки в правую нижнюю, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо он перемещается в соседнюю правую клетку, по команде вниз - в соседнюю нижнюю. При попытке выхода за границу квадрата Самокатик разваливается на части и прекращает движение. В каждой клетке квадрата записано целое число в диапазоне от -100 до 100. Самокатик - электрический; начальный уровень заряда его батареи указан в левой верхней клетке квадрата. При посещении очередной клетки уровень заряда батареи Самокатика изменяется на указанное в ней значение, но не может стать меньше 0 или больше 100. Это также относится к конечной клетке маршрута. Всякий раз, когда уровень заряда батареи Самокатика опускается до нуля, Пассажир спешивается и тащит его на себе. Определите максимально возможный уровень заряда батареи Самокатика в конечной клетке, если Пассажиру на протяжении всего маршрута:

A) запрещено спешиваться (Если добраться до конца невозможно, в ответ запишите -1);

B) разрешено спешиваться.

В ответе запишите сначала ответ на вопрос А, затем - ответ на вопрос B.

Вложения к задаче

10.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

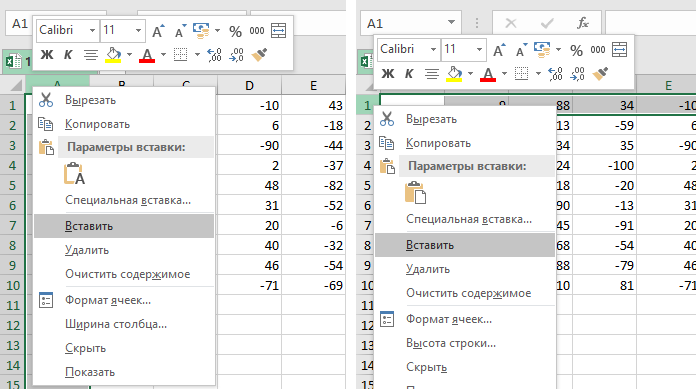
Выделяем всю таблицу и добавляем границы.

$PIC$

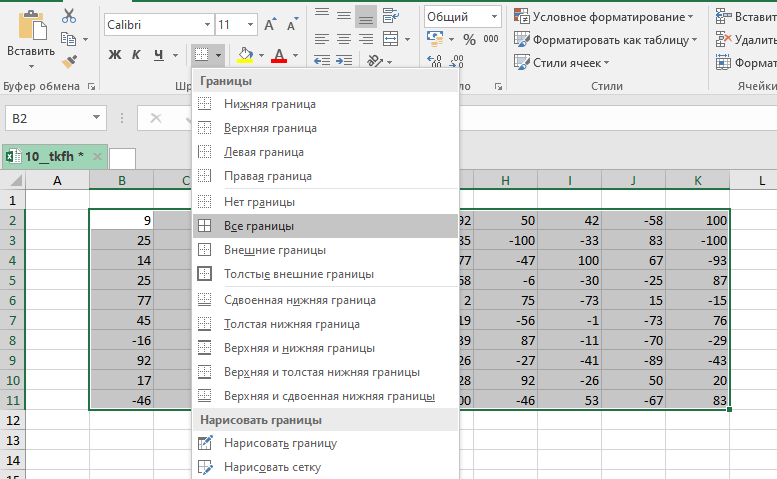
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
Решение для пункта A:
В начало маршрута (в нашем случае $B14$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C14$ записываем формулу =ЕСЛИ(МАКС(ЕСЛИ(C2+C13>0;C2+C13;-1000000);ЕСЛИ(C2+B14>0;C2+B14;-100000))>100;100;МАКС(ЕСЛИ(C2+C13>0;C2+C13;-1000000);ЕСЛИ(C2+B14>0;C2+B14;-100000))).

$PIC$

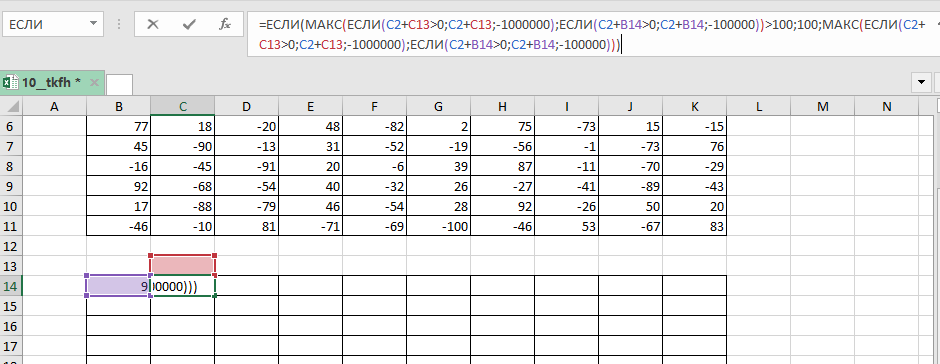
Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки.
Решение для пункта B:
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B26$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C26$ записываем формулу =ЕСЛИ(МАКС(ЕСЛИ(C2+C25>0;C2+C25;0);ЕСЛИ(C2+B26>0;C2+B26;0))>100;100;МАКС(ЕСЛИ(C2+C25>0;C2+C25;0);ЕСЛИ(C2+B26>0;C2+B26;0))).

$PIC$

Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки.

Запишем в ответ сначала первое полученное число, затем - второе.

Ответ: 100 100

Ошибка.
Попробуйте повторить позже

Задача 11#30160

Дан квадрат N $×$ N клеток, в каждой клетке которого записано целое число.

В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы квадрата робот не может. При этом ведётся подсчёт суммы по следующим правилам: число в очередной клетке, через которую проходит робот, включается в сумму, если оно больше числа в предыдущей клетке на пути робота. Если число в очередной клетке не больше числа в предыдущей, сумма не изменяется.

Число в начальной клетке всегда включается в сумму.

Необходимо переместить робота в правый нижний угол так, чтобы полученная сумма была максимальной.

В ответе запишите максимально возможную сумму.

Вложения к задаче

11.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

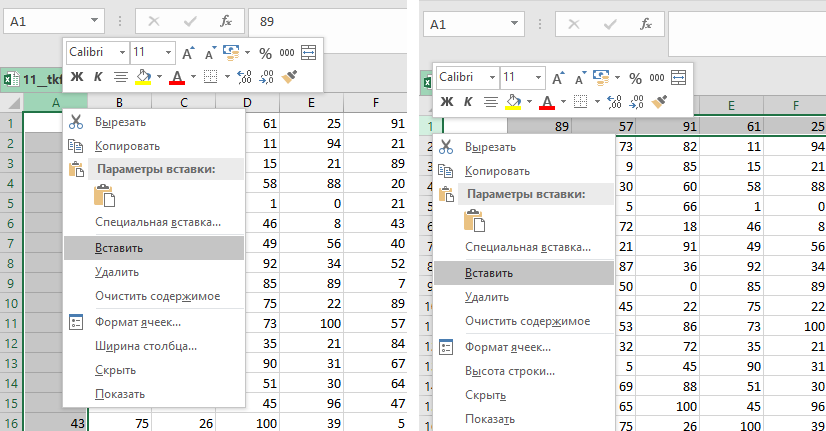
Выделяем всю таблицу и добавляем границы.

$PIC$

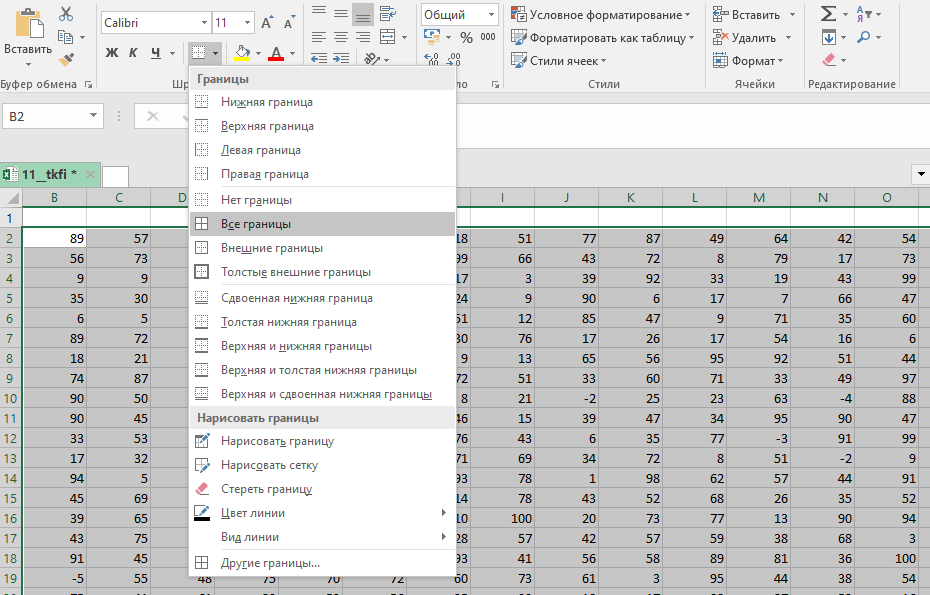
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B34$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C34$ записываем формулу =МАКС(ЕСЛИ(C2>C1;C33+C2;C33);ЕСЛИ(C2>B2;C2+B34;B34)).

$PIC$

Копируем её на всю таблицу.
Выписываем значение из правой нижней ячейки в ответ.

Ответ: 3042

Ошибка.
Попробуйте повторить позже

Задача 12#30163

Квадрат разлинован на N $×$ N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: влево или вниз. По команде влево Робот перемещается в соседнюю левую клетку, по команде вниз - в соседнюю нижнюю. Квадрат ограничен внешними стенами. В начальный момент запас энергии робота равен числу, записанному в стартовой клетке. После каждого шага робота запас энергии изменяется по следующим правилам: если число в очередной клетке больше или равно предыдущему, запас увеличивается на величину этого числа, если меньше - уменьшается на эту же величину. Определите максимальный запас энергии, который может быть у робота после перехода из правой верхней клетки поля в левую нижнюю.

Вложения к задаче

14.xlsx

Показать ответ и решение

Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

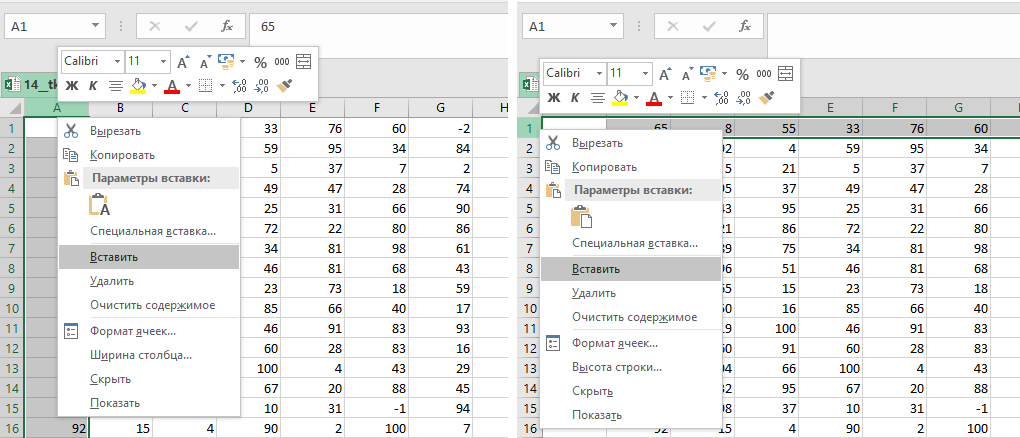
Выделяем всю таблицу и добавляем границы

$PIC$

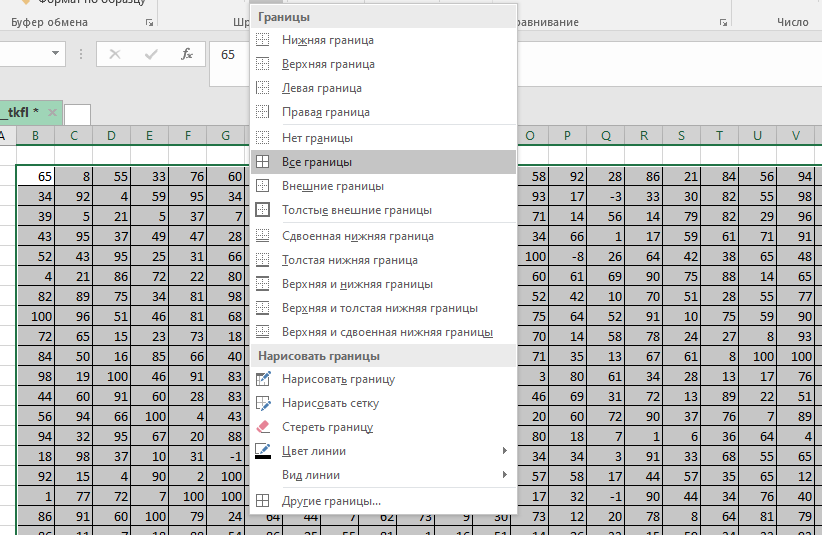
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат. В начало маршрута (в нашем случае $Z30$ ) записываем значение правой верхней клетки данной нам таблицы. В клетку $Y30$ записываем формулу =МАКС(ЕСЛИ(Y2>=Y1; Y29+Y2; Y29-Y2); ЕСЛИ(Y2>=Z2; Z30+Y2; Z30-Y2)).

$PIC$

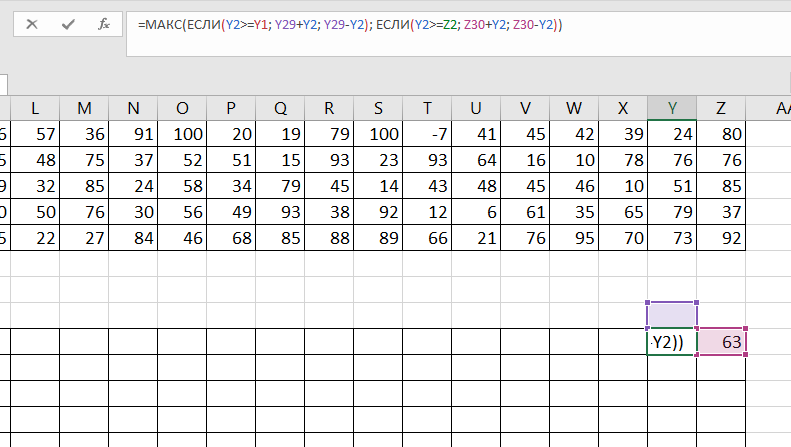
Копируем её на всю таблицу. Выписываем значение из левой нижней ячейки в ответ.

Ответ: 2613

Ошибка.
Попробуйте повторить позже

Задача 13#30164

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на $N × N$ клеток $(1 < N < 20)$ . Исполнитель Оборотень может перемещаться по клеткам вправо и вниз, но когда он делает $3$ хода в одном направлении (не обязательно подряд), он перевоплощается (если он был в первом стостоянии перевоплощается во второе, если во втором - в первое). При перевоплощении счетчики его ходов обнуляются. В первом своем состоянии по команде вниз Оборотень перемещается на одну клетку вниз, по команде вправо - на одну клетку вправо. Во втором состоянии при таких же командах он перепрыгивает через одну клетку в соответствующем направлении. При попытке выхода за границу квадрата Оборотень умирает. Перед каждым запуском Оборотня в каждой клетке квадрата лежит кусок мяса сытностью от $1$ до $100$ . Посетив клетку, Оборотень насыщается и съедает мясо (увеличивает значение насыщенности на сытность мяса); это также относится к начальной и конечной клетке маршрута Оборотня. Изначально значение насыщенности равно сытности мяса в стартовой клетке.

Откройте файл. Определите максимальное значение насыщенности, которого может достичь Оборотень, пройдя из верхней левой клетки в правую нижнюю.

Исходные данные представляют собой электронную таблицу размером $N × N$ , каждая ячейка которой соответствует клетке квадрата.

Вложения к задаче

15.xlsx

Показать ответ и решение

Откроем файл в Excel. Выделим все числа и скопируем их в текстовый документ. Для удобства с помощью комбинации Ctrl + H заменим большие отступы между числами одним пробелом. Получим вот такой файлик:

Теперь напишем программу для решения задачи:

#хватит 9 ходов вправо и 9 ходов вниз
f = open(’15.txt’)
a = []
for i in range(13):
    a.append([int(s) for s in f.readline().split()])
#стартуем из a[0][0], заканчиваем в a[12][12]

#генерируем маршрут из 18 ходов двоичной маской
#вправо - 1 вниз - 0
ma = -10**20
for k in range(2**18):
    t = k
    mask = []
    for j in range(18):
        mask.append(t%2)
        t//=2
    #погнали теперь пробежимся по этой маске!
    state = 1
    x,y=0,0
    right,down = 0,0
    s = a[0][0]
    for j in range(18):
        if mask[j]==0:
            y+=state
            right+=1
        else:
            x+=state
            down+=1
        if right==3 or down==3:
            state = 3-state
            right = 0
            down = 0
        if x>12 or y>12:
            break
        s+=a[x][y]
        if x==12 and y==12:
            #успешный конец миссии!
            if s>ma:
                                                                                                     
                                                                                                     
                ma = s
            break
print(ma)

Ответ: 1238

Ошибка.
Попробуйте повторить позже

Задача 14#54241

Квадрат разлинован на $N × N$ клеток $(2 < N < 19)$ . В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 1.

Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый имеет две команды – вверх и вправо, второй – вниз и вправо, которые, соответственно, перемещают исполнитель на одну клетку вверх, вниз или вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке, исполнитель НИЗ – в левой верхней.

Откройте файл. Какой из исполнителей соберет большее количество монет в результате своей работы, если известно, что каждый из них запрограммирован собрать максимальное количество монет?

В ответе запишите без пробелов и разделителей сначала название исполнителя (ВЕРХ илм НИЗ), а затем максимальную сумму, которую он соберет.

Вложения к задаче

6.xlsx

Показать ответ и решение

Нам дано поле 14 на 14, создадим рядом еще одно поле такого же размера (ячейки $A16 : N 29$ ). Сначала найдем максимальную сумму для исполнителя НИЗ.

В левую верхнюю клетку нового поля, записываем значение из левой верхней клетки исходного поля – 48.

Заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля, прибавим значение из клетки $B1$ , сделаем это с помощью формулы:

=A16+B1

Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.

Найдем максимальное значение суммы. Рассмотрим ячейку $B2$ , в нее мы можем попасть из $B1$ и $A2$ , тогда, чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из которых можем попасть в эту. В ячейку $B17$ запишем формулу:

=МАКС(A17;B16)+B2

Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальной суммой, которую может собрать исполнитель НИЗ – 1930.

Теперь найдем максимальную сумму, которую может собрать исполнитель ВЕРХ. Для этого будем использовать уже созданное поле (ячейки $A16 : N 29$ ), отчистим его.

В левую нижнюю ячейку нового поля, записываем значение из левой нижнец клетки исходного поля – 41.

Заполним значениями нижнюю строку и левый столбец. Сделаем это по аналогии с тем как мы заполняли верхнюю строку и левый столбец в решении для исполнителя НИЗ.

Найдем максимальное значение суммы. Рассмотрим ячейку $B13$ , в нее мы можем попасть из $B14$ и $A13$ , тогда, чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из которых можем попасть в эту. В ячейку $B28$ запишем формулу:

=МАКС(A28;B29)+B13

Теперь растянем эту формулу на все свободные ячейки поля. В правом верхнем углу будет число, которое является максимальной суммой, которую может собрать исполнитель ВЕРХ – 1708.

Тогда ответ будет НИЗ1930.

Ответ: НИЗ1930

Ошибка.
Попробуйте повторить позже

Задача 15#54242

Дан файл, в котором есть два поля – красное и зеленое. Зеленое поле – поле подзарядки, проходя по его клетке самокат Курьера заряжается на то число условных едениц, которое указано в этой клетке. Зарядка начинается в левой верхней клетке и заканчивается в правой нижней клетке зеленого поля. Красное поле – поле доставки, по нему Курьеру необходимо доставить заказ из левой верхней клетки в правую нижнюю. Проходя по клетке красного поля, самокат Курьера разряжается на то число условных едениц, которое указано в этой клетке. Если заряд становится меньше или равен нулю, то курьер не может двигаться дальше.

За один ход Курьер может переместиться на одну клетку вправо или на одну клетку вниз. Выходить за пределы полей Курьер не может. В начальный момент заряд самоката равен нулю. Определите, сможет ли курьер доставить заказ, если сначала пройдет по зеленому полю, а потом по красному.

Курьер очень предусмотрительный, поэтому старается зарядить свой самокат как можно больше, а при доставке старается потратить как можно меньше энергии.

В ответе запишите без пробелов и разделителей ДА и остаток заряда если сможет и НЕТ и количество заряда которое ему не хватило, если заказ не будет доставлен.

Вложения к задаче

7.xlsx

Показать ответ и решение

Сначала найдем число у. е. на которое самокат Курьера сможет зарядиться пройдя по Зеленому полю, так как Курьер предусмотрительный, то будем искать максимальное число у. е. .

Нам дано Зеленое поле 10 на 10, создадим рядом еще одно поле такого же размера (ячейки $A23 : J32$ ). В левую верхнюю клетку нового поля, записываем значение из левой верхней клетки исходного поля – 24.

Сначала заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля, прибавим значение из клетки $B1$ , сделаем это с помощью формулы:

=A23+B1

Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.

Найдем максимальное значение суммы. Рассмотрим ячейку $B2$ , в нее мы можем попасть из $B1$ и $A2$ , тогда, чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из которых можем попасть в эту. В ячейку $B24$ запишем формулу:

=МАКС(A16;B15)+B2

Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальным количеством у. е., на которое Курьер может зарядить самокат – 821.

Теперь идем доставлять заказ, так как Курьер предусмотрительный, то будем искать минимальное числ у. е., которое можно потратить пройдя по Красному полю.

Нам дано Красное поле 10 на 10, создадим рядом еще одно поле такого же размера (ячейки $K33 : T42$ ). В левую верхнюю клетку нового поля, записываем значение равное заряд самоката минус значение из левой верхней клетки исходного поля: =J32-K11.

Далее заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля, отнимем значение из клетки $L11$ , сделаем это с помощью формулы:

=K33-L11

Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.

Так как мы хотим потратить как можно меньше энергии, то в каждую следующую клетку следует попадать из клетки с максимальным числом (остатком энергии). Запишем в клетку $L34$ формулу и растянем на весь необходимый диапазон.

=МАКС(K34;L33)-L12

В правом нижнем углу будет число, которое является максимальным количеством у. е., которое останется после доставки – 508.

Ответ: ДА508

Ошибка.
Попробуйте повторить позже

Задача 16#56319

Задание выполняется с использованием прилагаемых файлов.

Квадрат разлинован на $N × N$ клеток $(1 < N < 12)$ . Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. В квадрате есть клетки, помеченные зеленым. В них сидят котики. Робот очень любит котиков и обязательно пройдет через эти клетки, чтобы погладить котиков. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

Откройте файл. Определите максимальную денежную сумму, которую может собрать Робот. В ответ запишите одно число — максимальную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.

Исходные данные представляют собой электронную таблицу размером $N × N$ , каждая ячейка которой соответствует клетке квадрата.

Вложения к задаче

18.xlsx

Показать ответ и решение

Так как нам обязательно нужно пройти через зелёные клетки, то в исходной таблице добавим в каждую по $1000000$ .

$PIC$

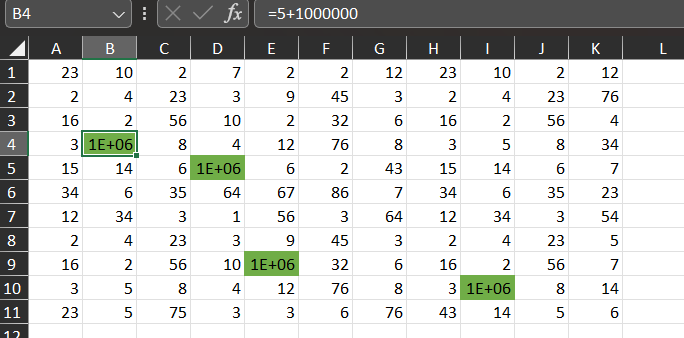
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить).

$PIC$

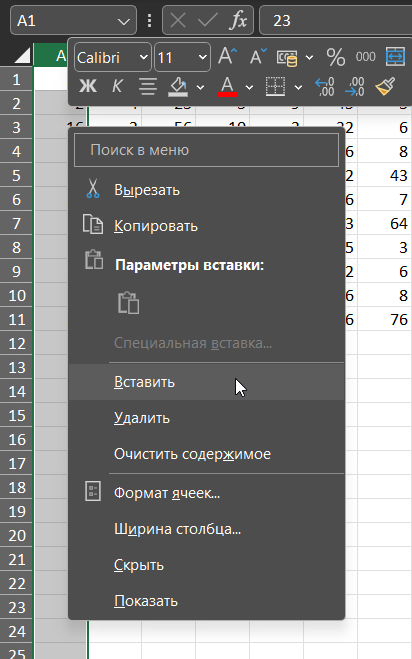
Выделяем всю таблицу и добавляем границы.

$PIC$

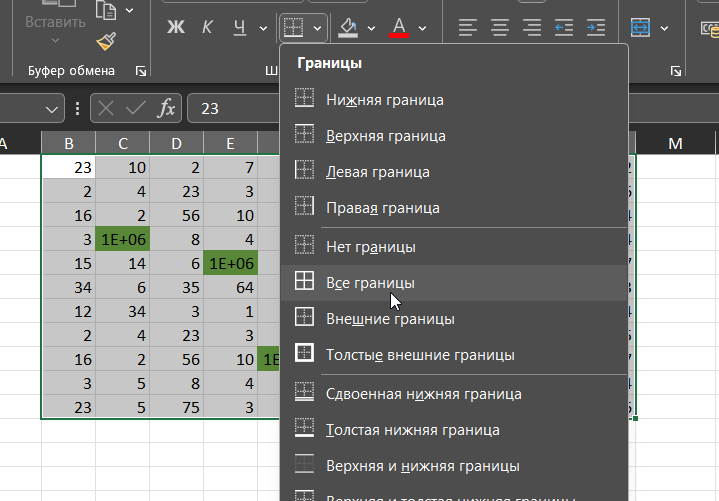
Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат.
В начало маршрута (в нашем случае $B14$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C14$ записываем формулу =МАКС(C13;B14)+C1

$PIC$

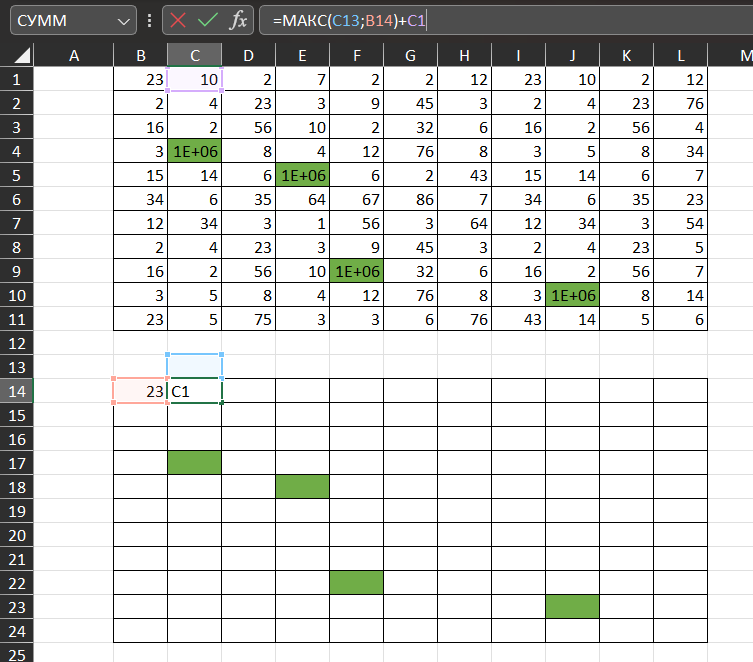
Вставляем эту формулу во все оствшиеся клетки таблицы. Не забываем, что мы специально добавили несколько миллионов. Так как у нас $4$ зеленые клетки, то запишем в любую свободную ячейку формулу =L24-4000000, полученное число и есть ответ.

Ответ: 427

Ошибка.
Попробуйте повторить позже

Задача 17#56473

Квадрат разлинован на $N ×N$ клеток $(1 < N < 17).$ Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается.

В начальный момент запас энергии робота равен числу, записанному в стартовой (левой верхней) клетке. После каждого шага робота запас энергии изменяется по следующим правилам: если число в очередной клетке больше или равно предыдущему, запас увеличивается на величину этого числа, если меньше — уменьшается на эту же величину.

Откройте файл. Определите минимальный и максимальный запас энергии, который может быть у робота после перехода из левой верхней клетки поля в правую нижнюю. В ответ запишите два числа через пробел — минимальный и максимальный запас энергии, который может быть собран роботом.

Исходные данные представляют собой электронную таблицу размером $N × N$ , каждая ячейка которой соответствует клетке квадрата.

Вложения к задаче

18_new.xlsx

Показать ответ и решение

Копируем таблицу и с помощью специальной вставки ( $Ctrl+ Alt+ V$ ) вставляем только её формат. Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец $A$ и выбираем Вставить) и пустую строку перед самой первой (нажимаем правой кнопкой мыши на строку $1$ и выбираем Вставить).

$PIC$

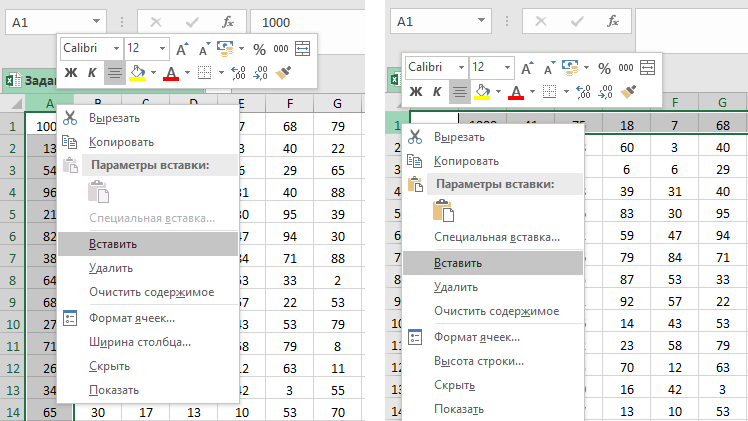
В начало маршрута (в нашем случае $B22$ ) записываем значение левой верхней клетки данной нам таблицы. В клетку $C22$ записываем формулу

=МИН(ЕСЛИ(C2>=B2;B22+C2;B22-C2);ЕСЛИ(C2>=C1;C21+C2;C21-C2)) и копируем её на всю таблицу. Выписываем значение из правой нижней ячейки. Заменим все МИН на МАКС и также выпишем значение из правой нижней клетки.
Запишем в ответ сначала минимальный запас энергии, затем через пробел - максимальный.

Ответ: 851 2065

Ошибка.
Попробуйте повторить позже

Задача 18#57335

Квадрат разлинован на $N × N$ клеток $(2 < N < 19)$ . В каждой клетке лежат монеты, количество которых соответствует записанному числу. Количество монет не может быть меньше 1.

Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый имеет две команды – вверх и вправо, второй – вниз и вправо, которые, соответственно, перемещают исполнитель на одну клетку вверх, вниз или вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке, исполнитель НИЗ – в левой верхней.

Откройте файл. Какой из исполнителей соберет большее количество монет в результате своей работы, если известно, что каждый из них запрограммирован собрать максимальное количество монет?

В ответе запишите модуль разницы между максимальной суммой, которую может собрать исполнитель НИЗ, и максимальной суммой, которую может собрать исполнитель ВЕРХ.

Вложения к задаче

18-6.xlsx

Показать ответ и решение

Нам дано поле 14 на 14, создадим рядом еще одно поле такого же размера (ячейки $A16 : N 29$ ). Сначала найдем максимальную сумму для исполнителя НИЗ.

В левую верхнюю клетку нового поля, записываем значение из левой верхней клетки исходного поля – 45.

Заполним значениями верхнюю строку. Для этого к значенею из левой верхней клетки нового поля, прибавим значение из клетки $B1$ , сделаем это с помощью формулы:

=A16+B1

Теперь, чтобы заполнить оставшиеся ячейки верхней строки нового поля, растянем эту формулу на всю строку. Подобным образом заполним левый столбец нового поля.

Найдем максимальное значение суммы. Рассмотрим ячейку $B2$ , в нее мы можем попасть из $B1$ и $A2$ , тогда, чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из которых можем попасть в эту. В ячейку $B17$ запишем формулу:

=МАКС(A17;B16)+B2

Теперь растянем эту формулу на все свободные ячейки поля. В правом нижнем углу будет число, которое является максимальной суммой, которую может собрать исполнитель НИЗ – 2065.

Теперь найдем максимальную сумму, которую может собрать исполнитель ВЕРХ. Для этого будем использовать уже созданное поле (ячейки $A16 : N 29$ ), отчистим его.

В левую нижнюю ячейку нового поля, записываем значение из левой нижнец клетки исходного поля – 84.

Заполним значениями нижнюю строку и левый столбец. Сделаем это по аналогии с тем как мы заполняли верхнюю строку и левый столбец в решении для исполнителя НИЗ.

Найдем максимальное значение суммы. Рассмотрим ячейку $B13$ , в нее мы можем попасть из $B14$ и $A13$ , тогда, чтобы в этой клетке суммы была максимальной, необходимо выбрать максимальную сумму из тех двух клеточек, из которых можем попасть в эту. В ячейку $B28$ запишем формулу:

=МАКС(A28;B29)+B13

Теперь растянем эту формулу на все свободные ячейки поля. В правом верхнем углу будет число, которое является максимальной суммой, которую может собрать исполнитель ВЕРХ – 2064.

Тогда ответ будет 2065 - 2064 = 1.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 19#59625

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на $20$ * $20$ клеток. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх - в соседнюю верхнюю. При попытке выхода за границу квадрата Робот умирает. В квадрате могут быть ямы (помечены красным). Попадая в ямку Робот не может из нее выбраться и от горя ломается. В квадрате есть клетки, помеченные зеленым, в них сидят котики. Робот очень любит котиков, он старается пройти через эти клетки, чтобы погладить их. Первостепенная задача – погладить как можно больше котиков. К сожалению, котики расположены в таблице так, что робот не сможет погладить всех котиков, но он попытается погладить как можно большее количество котиков.

Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

При условии, что Робот погладил максимально возможное количество котиков и не упал в яму, определите максимальную денежную сумму, которую может собрать Робот. В ответ запишите одно число - максимальную сумму, которую может собрать Робот.

Вложения к задаче

Книга 5.xlsx

Показать ответ и решение

Зеленые клетки мы обязаны пройти - значит прибавим к ним $1000000$ , чтобы мы точно при поиске максимума из клеток прошли через нее(потом вычтем лишнее). С красными клетками поступим также, но чуть по-другому - присвоим им значение $− 1000000$ . Так мы в них не наступим при написании дальнейшей формулы.

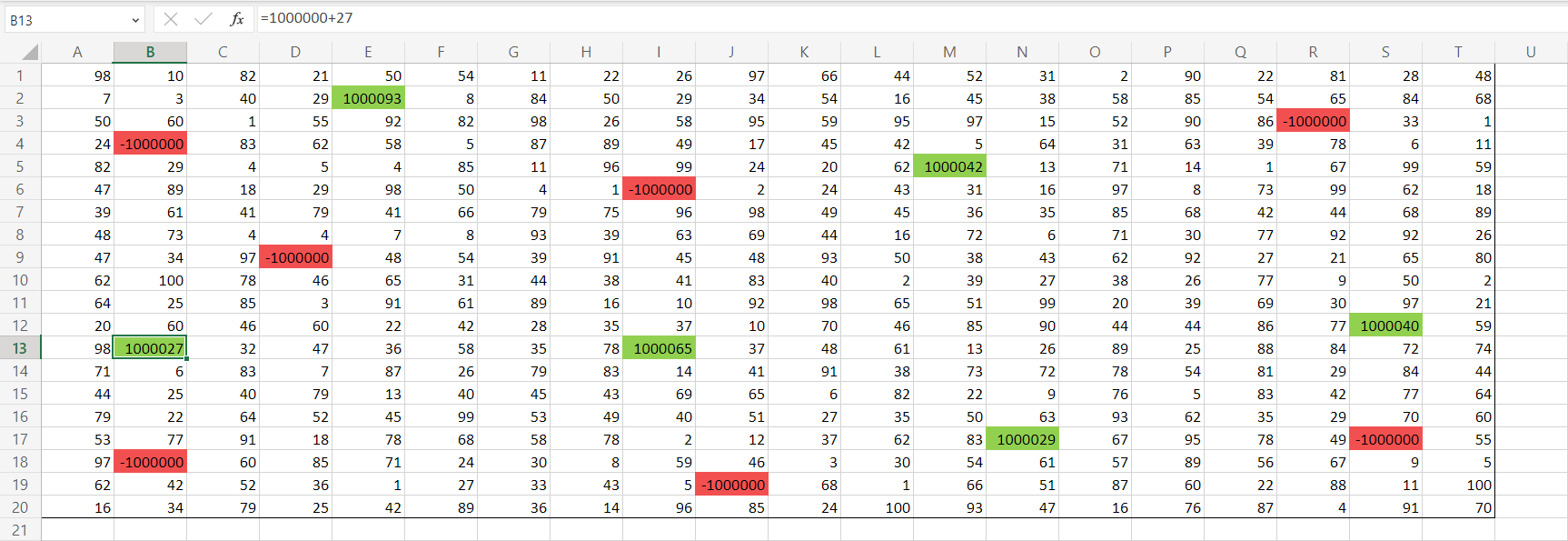
Теперь приступаем к нашей формуле. Выбираем максимум среди прошлых и прибавляем настоящие.

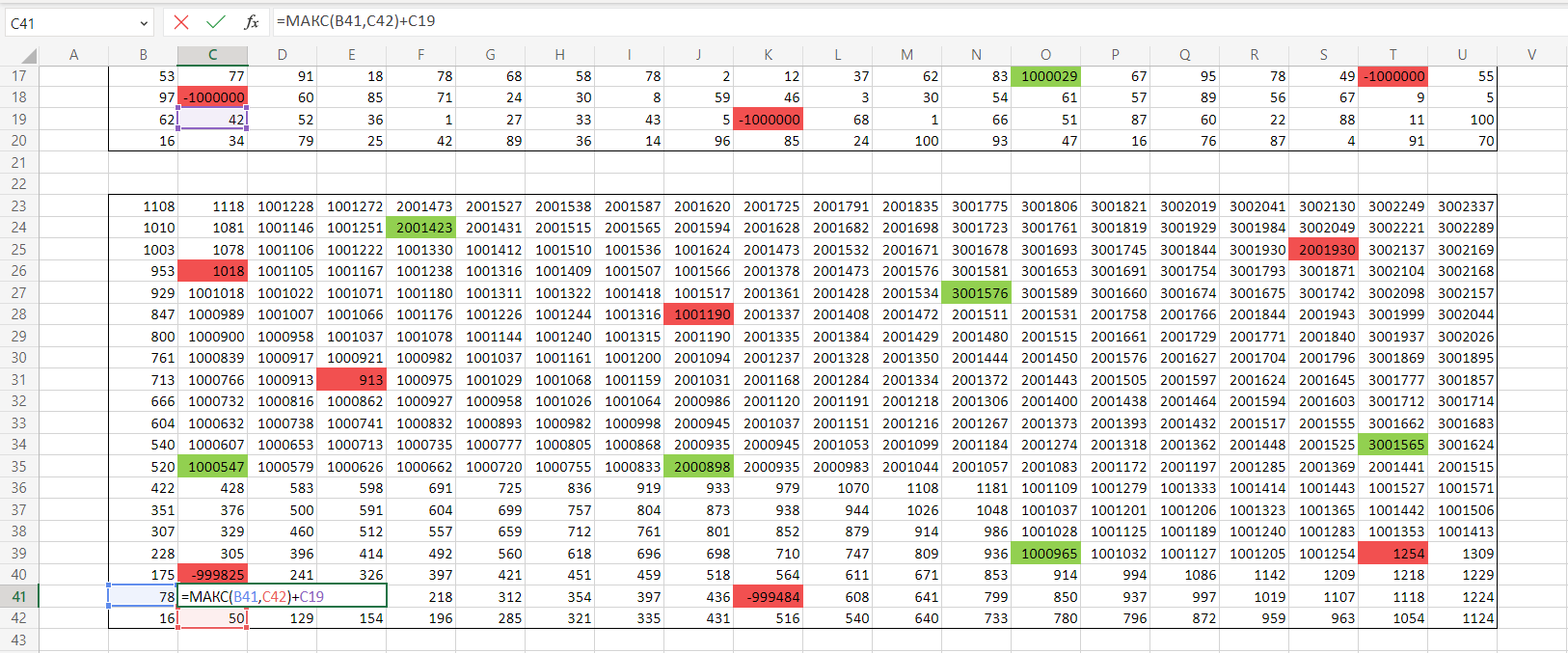
Скопируем формулу на все ячейки таблицы. Смотрим самое верхнее правое значение - оно больше на 3 миллиона. Вычитаем их и получаем наш ответ.

Ответ: 2337

Ошибка.
Попробуйте повторить позже

Задача 20#59626

Задание выполняется с использованием прилагаемых файлов

Квадрат разлинован на $N$ * $N$ клеток. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз - в соседнюю нижнюю. Робот изначально находится в левом верхнем углу. При попытке выхода за границу квадрата Робот умирает. В квадрате могут быть ямы (помечены красным). Попадая в ямку Робот не может из нее выбраться и от горя ломается. В квадрате есть клетки, помеченные зеленым, в них сидят котики. Робот очень любит котиков, он старается пройти через эти клетки, чтобы погладить их. К сожалению, котики расположены в таблице так, что робот не сможет погладить всех котиков. Но его первостепенная задача – погладить как можно большее количество котиков!

Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от $1$ до $100$ . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.

При условии, что Робот погладил максимально возможное количество котиков и не упал в яму, определите максимальную денежную сумму, которую может собрать Робот. В ответ запишите одно число - максимальную сумму, которую может собрать Робот.

Вложения к задаче

Книга 5.xlsx

Показать ответ и решение

Зеленые клетки мы обязаны пройти - значит прибавим к ним $1000000$ , чтобы мы точно при поиске максимума из клеток прошли через нее(потом вычтем лишнее). С красными клетками поступим также, но чуть по-другому - присвоим им значение $− 1000000$ . Так мы в них не наступим при написании дальнейшей формулы.

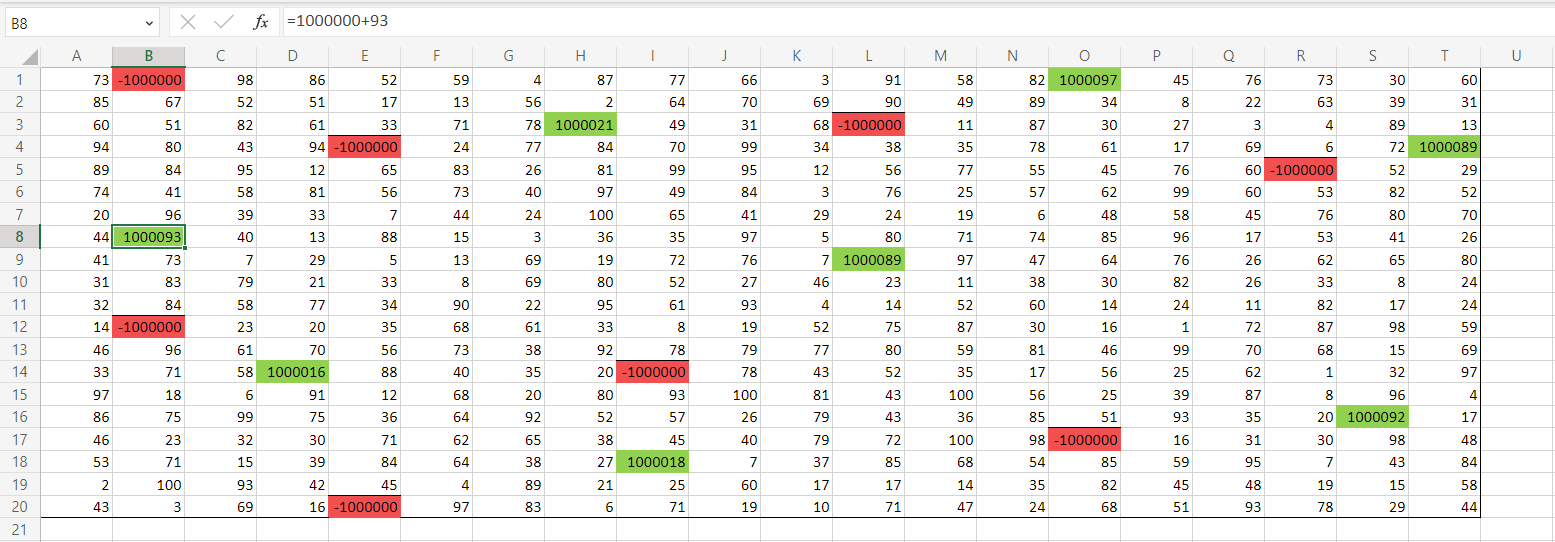
Теперь приступаем к нашей формуле. Выбираем максимум среди прошлых и прибавляем настоящие.

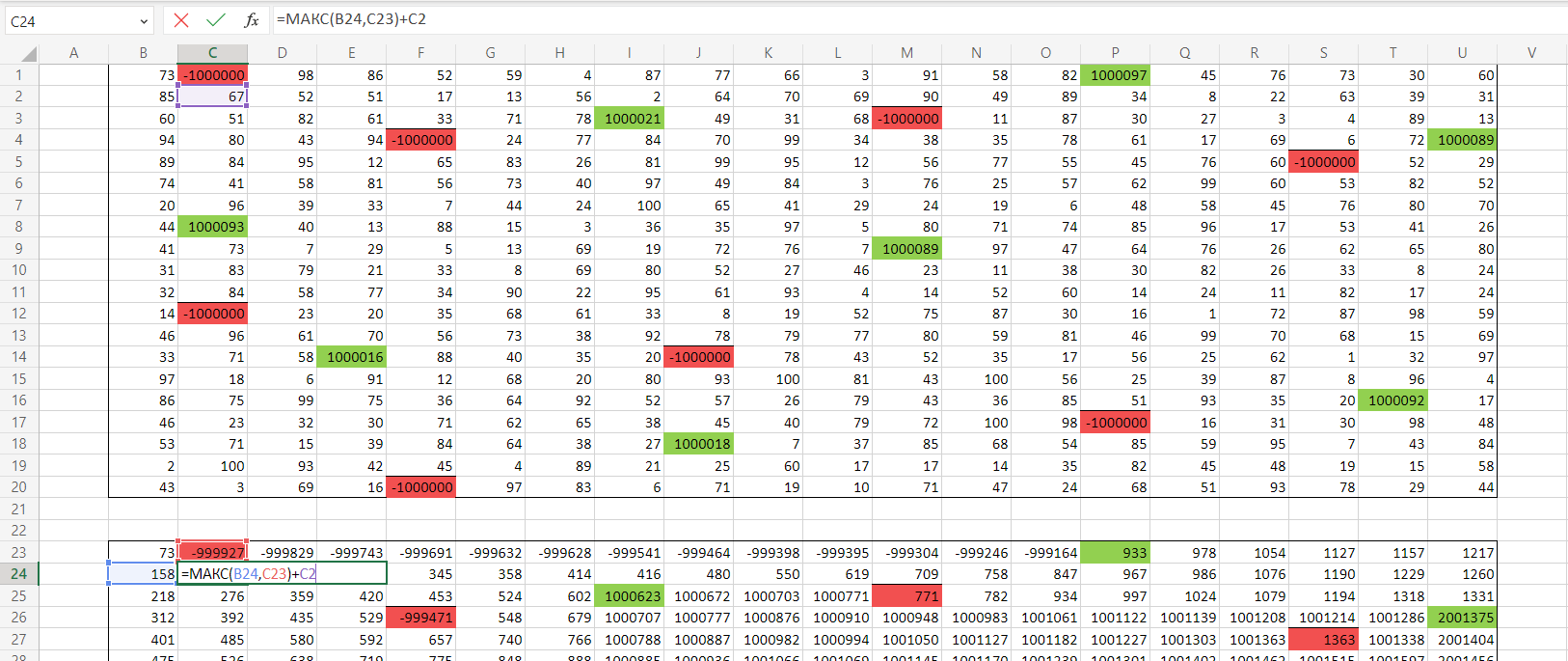
Скопируем формулу на все ячейки таблицы. Смотрим самое нижнее правое значение - оно больше на 3 миллиона. Вычитаем их и получаем наш ответ.

Ответ: 2673

18.06 Прочие прототипы