Планиметрия на Бельчонке
Ошибка.
Попробуйте повторить позже
В треугольнике на стороне
выбрана точка
Около треугольников
и
описаны окружности
и
соответственно. Окружность
пересекает сторону
в точке
а окружность
пересекает сторону
в точке
Известно, что
Докажите, что
Источники:
Подсказка 1
Давайте попробуем применить условие на описанные около треугольников окружности. Пусть равные по условию задачи углы будут равны α. Поищем одинаковые уголки, с учётом того, что наши углы для этих окружностей — вписанные.
Подсказка 2
∠AFD опирается на ту же дугу, что и ∠ABD, значит, они равны. Тоже самое можно сказать и про ∠EBD и ∠ECD. Картинка симметрична относительно выбора угла, значит, можем сделать аналогичные выводы для ∠DBC.
Подсказка 3
Мы хотим доказать равенство AE и CF. Возможно, оно получится из равенства каких-то треугольников.
Подсказка 4
Посмотрим на треугольники AED и CFD. С учётом посчитанных ранее углов углов, что у них общего?
Подсказка 5
Углы FAD и AFD равны, значит, треугольник FAD — равнобедренный. Аналогично для треугольника CED. Равные стороны треугольников лежат в искомых треугольниках, значит, мы уже получили две пары равных сторон. Осталось понять, почему углы между этими сторонами окажутся равны.
Подсказка 6
Например, потому что каждый из углов — внешний для треугольника AFD или DEC, которые имеют равные углы при основаниях.
Пусть Так как
и
опираются на дугу
окружности
то
Кроме того,
так как они описаются на дугу
окружности
В треугольнике
углы при основании
равны
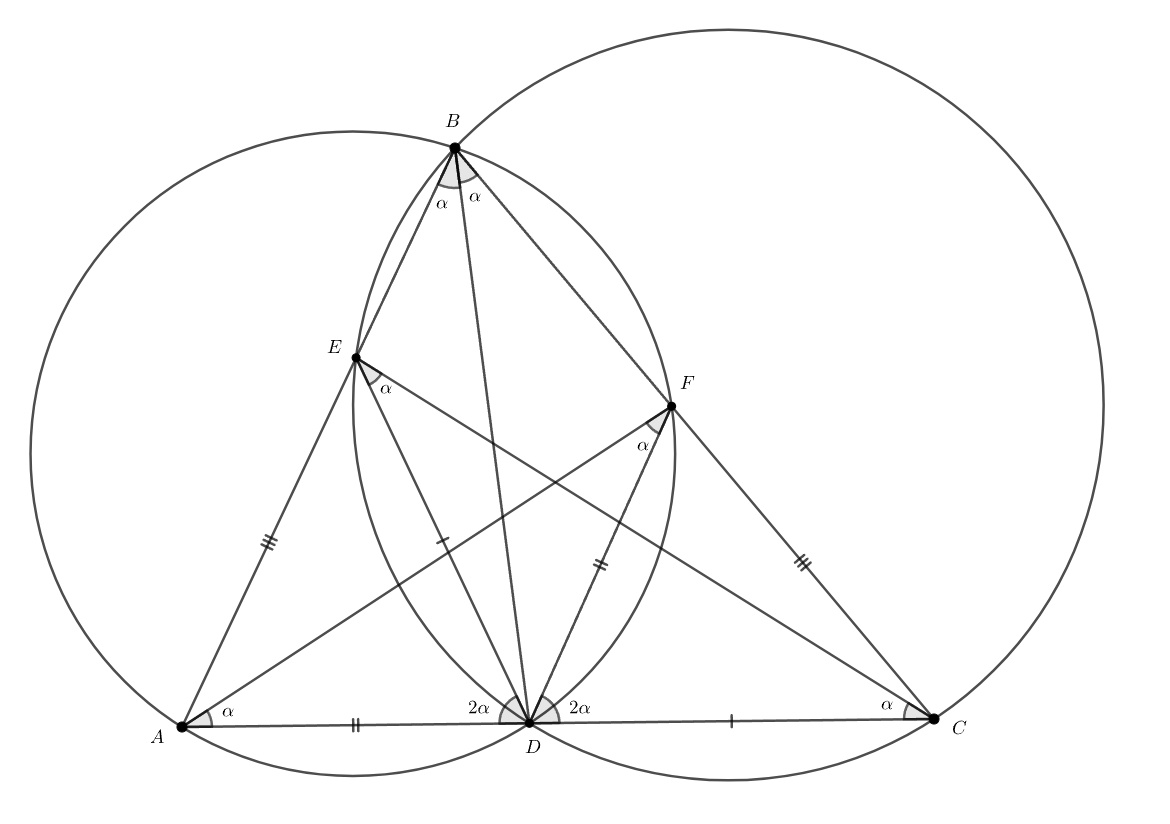
Кроме того, как внешний угол треугольника
Аналогично для треугольника
В итоге,
Поскольку треугольники
и
— равнобедренные,
Следовательно, Выходит, что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




