Графика. Функции с модулем: галочка, корыто и другие

Рассмотрим графики функций

Точки пересечения этих графиков и будут решением уравнения.

Сначала построим график функции

Если то

Если же то

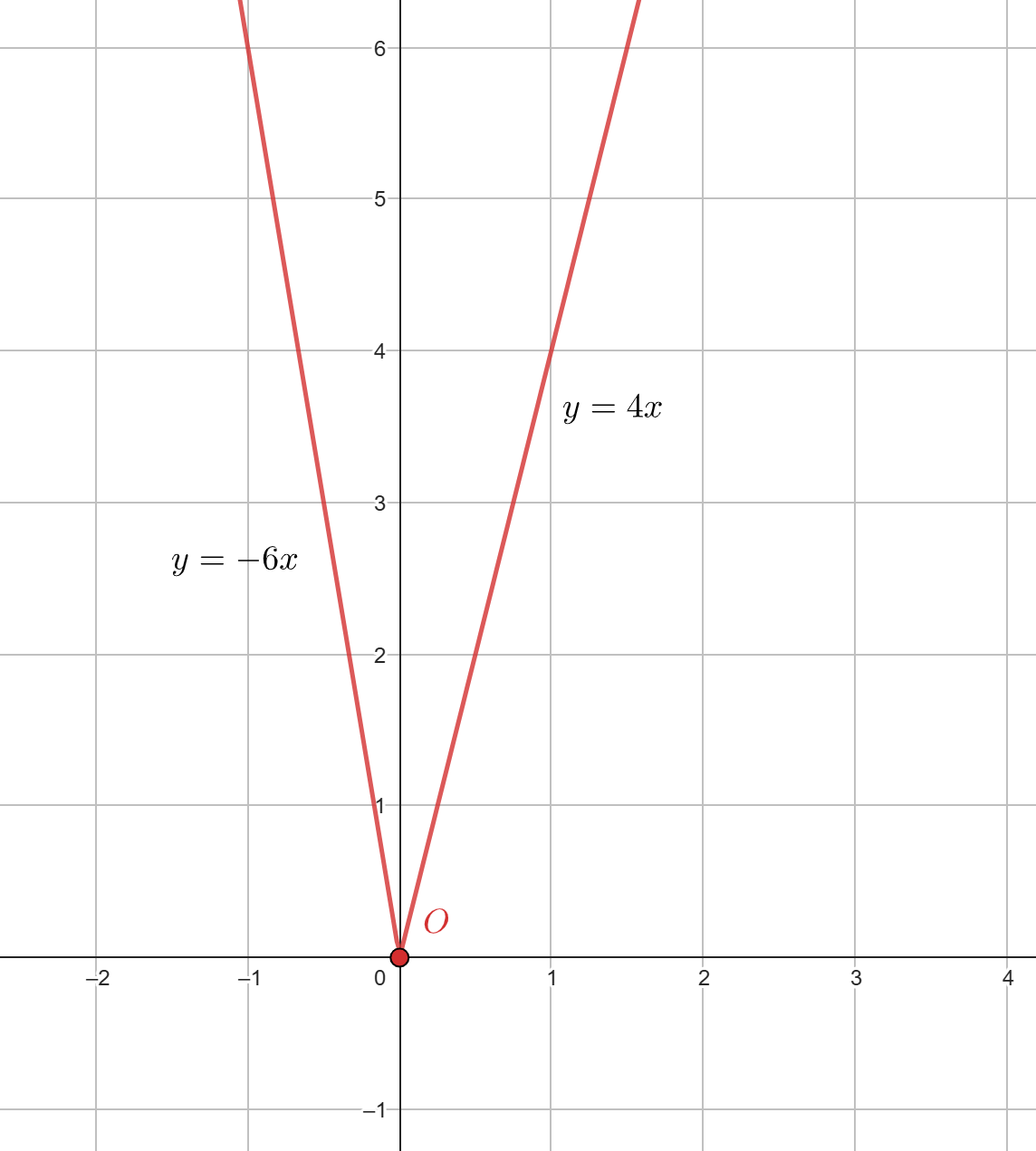
Заметим, что — это прямая смещённая на 4 единицы влево вдоль оси То есть график функции пересекает ось абсцисс в точке а от параметра зависит угол наклона прямой.

Найдем точку пересечения прямых и

Отсюда следует, что при прямые пересекаются не ниже оси абсцисс, а, значит, при таких значениях график пересекает правую часть графика

Теперь найдем точку пересечения прямых и

Отсюда следует, что при прямые пересекаются не ниже оси абсцисс, а, значит, при таких значениях график пересекает левую часть графика

Рассмотрим расположение графиков в зависимости от значения

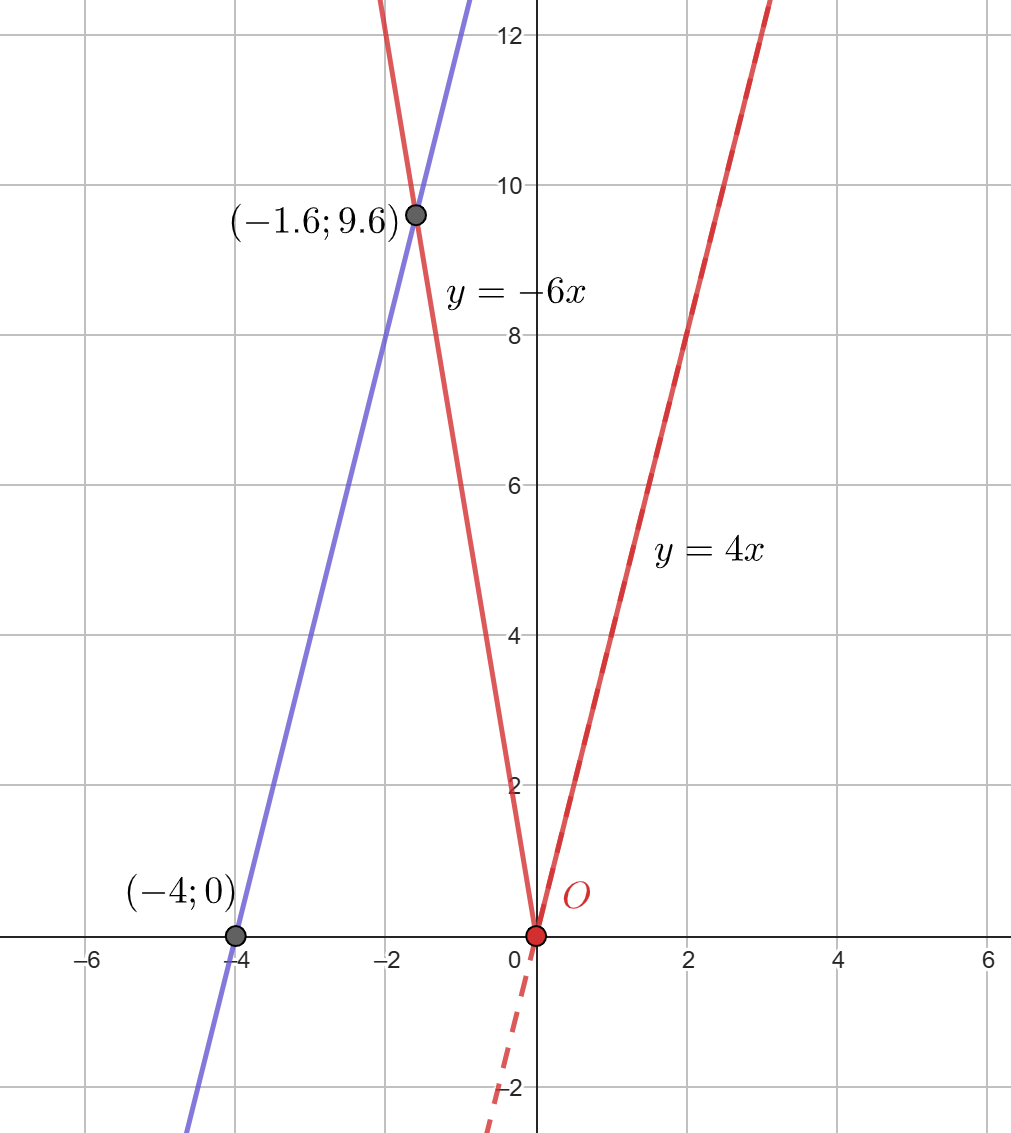
При При таких значениях график будет пересекать прямую выше а прямую — ниже, то есть графики и будут иметь ровно одну точку пересечения.

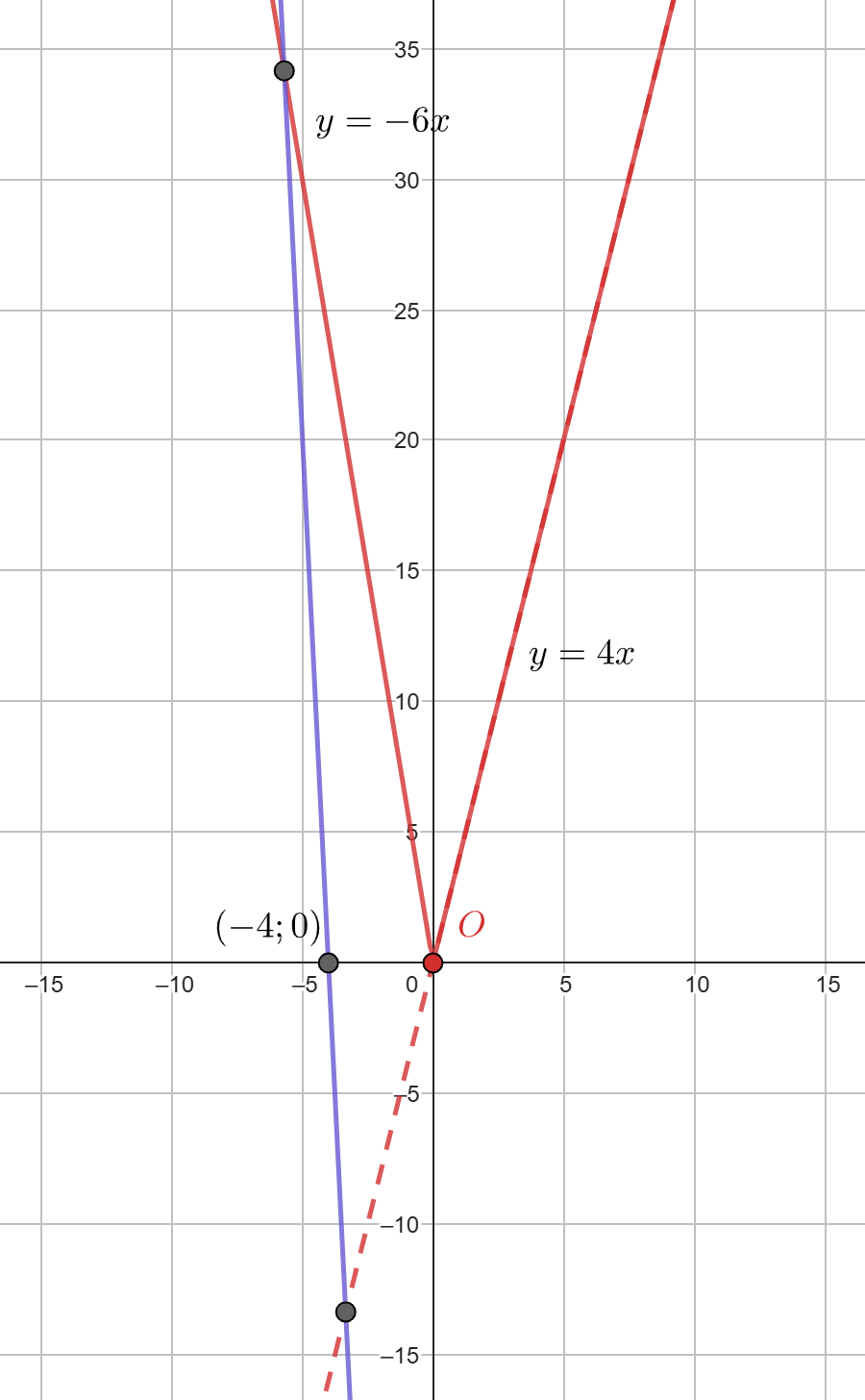
При При этом значении прямые и параллельны, то есть не имеют точек пересечения, а прямые и пересекаются в точке что выше а, значит, и имеют ровно одну точку пересечения.

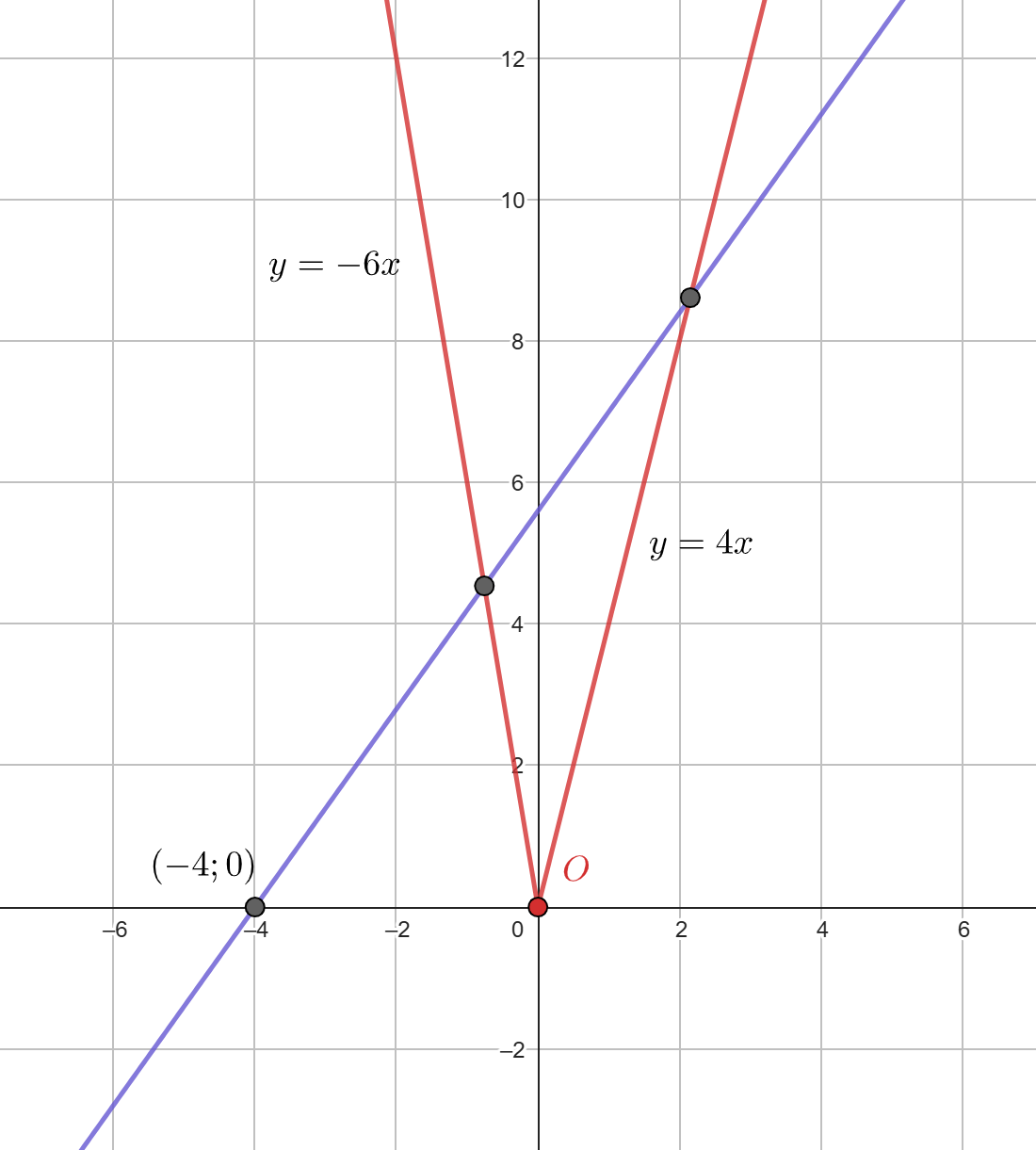
При В этом случае прямая пересекает и левую, и правую часть графика откуда и имеют две точки пересечения.

При График — горизонтальная прямая, совпадающая с прямой поэтому и имеют единственную точку пересечения — точку

При перескает прямые и ниже оси асбцисс, поэтому не имеет общих точек с

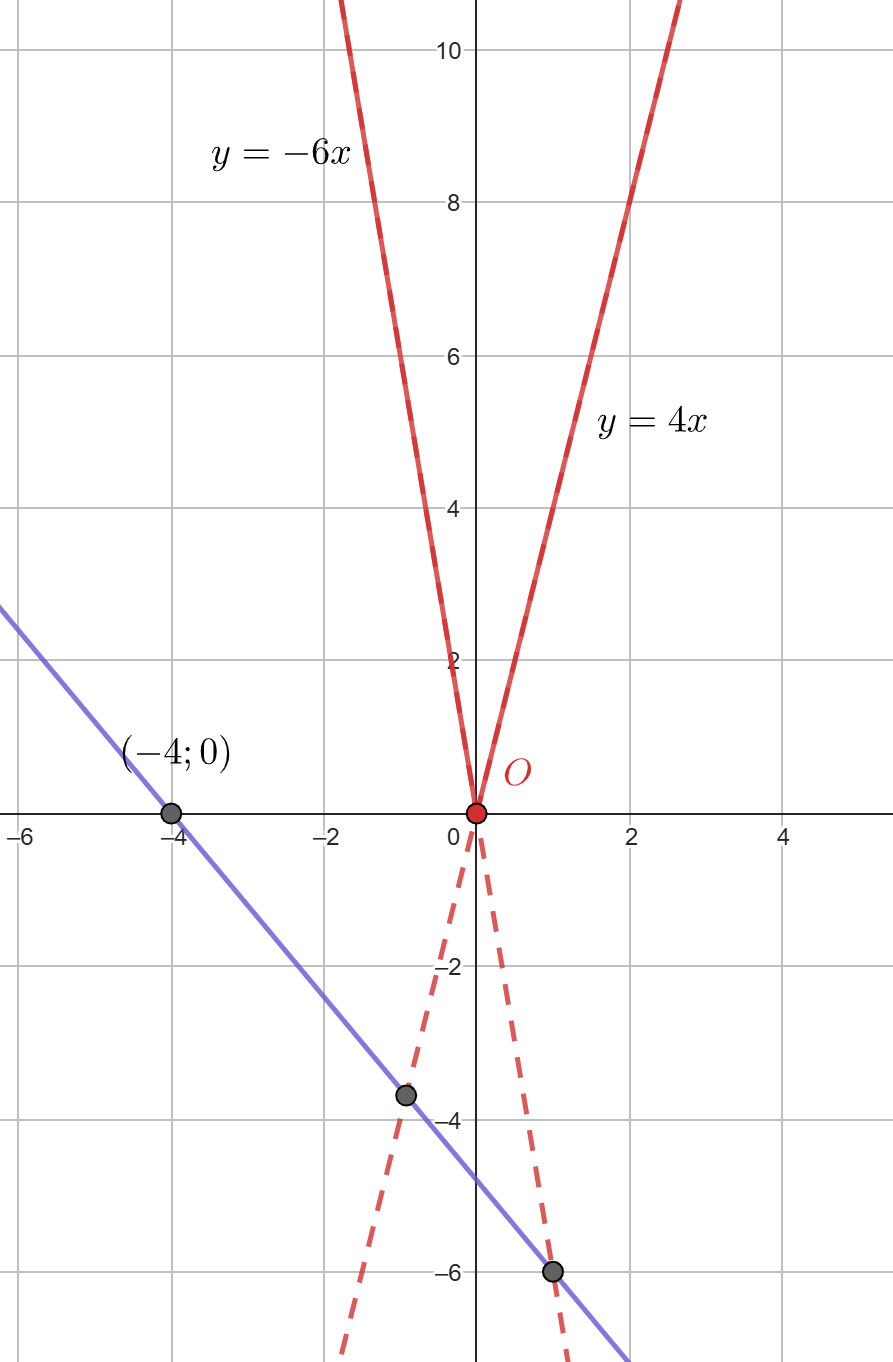
При прямые и параллельны, то есть не имеют точек пересечения, а прямые и пересекаются ниже а значит и не имеют общих точек.

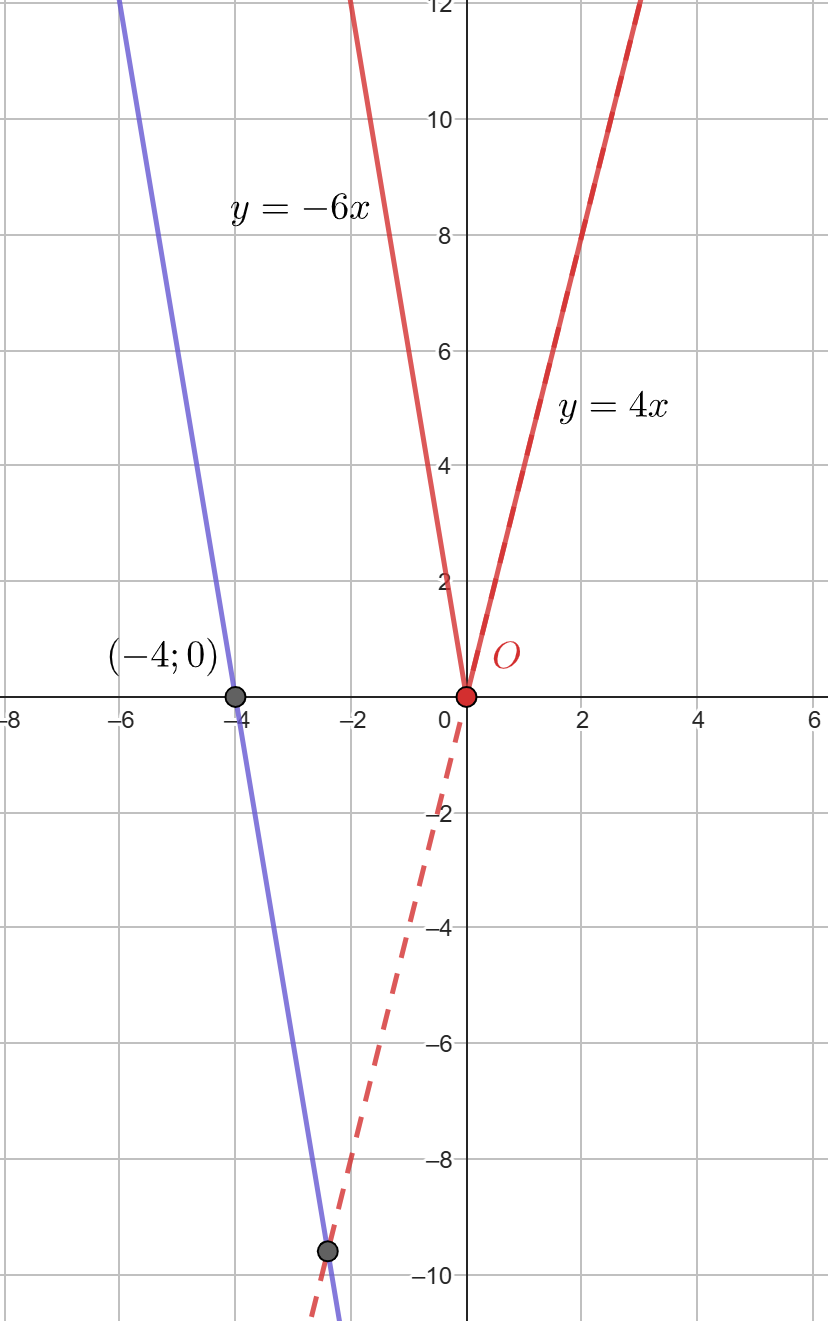
Наконец, при прямая пересекает ниже а — ниже, а, значит, и имеют ровно одну точку пересечения.

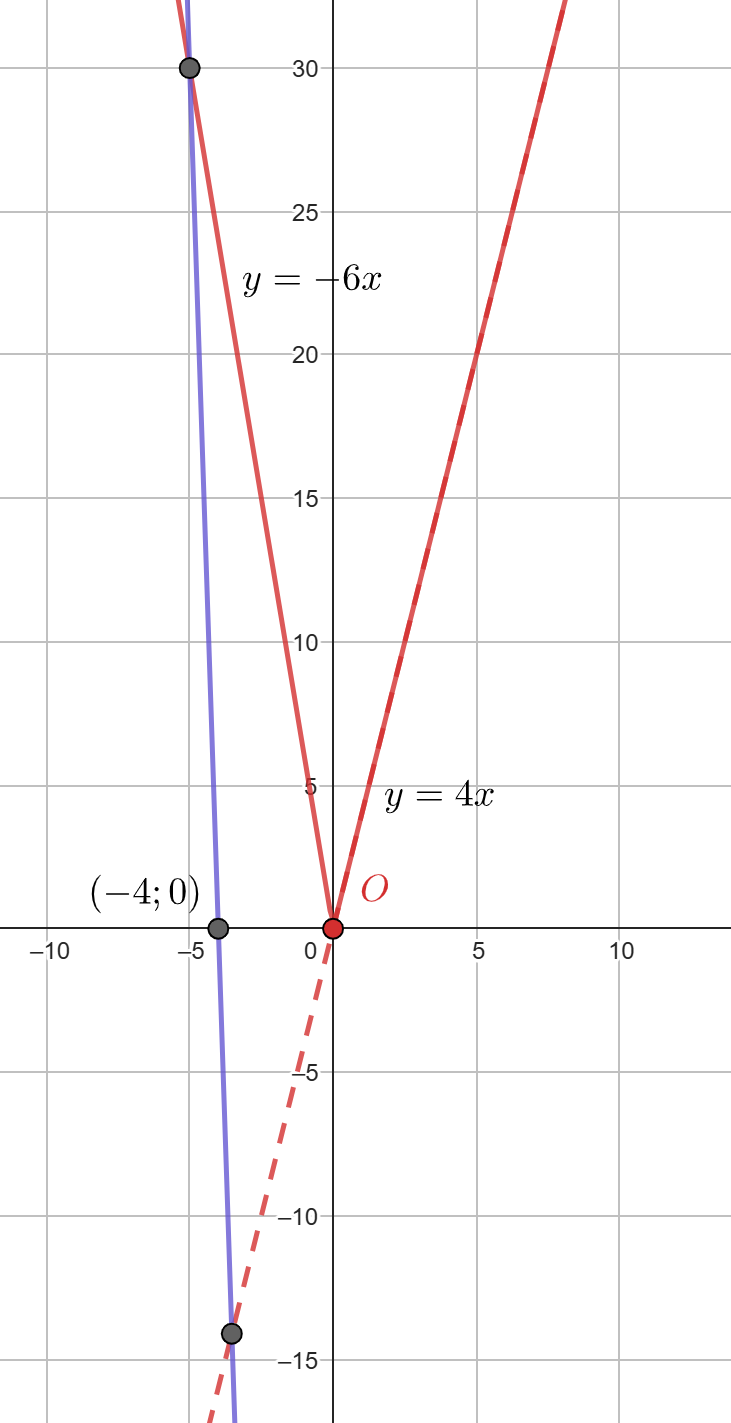
Итак, мы получили, что графики и имеют ровно одну точку пересечения при