Графика. Функции с модулем: галочка, корыто и другие
Ошибка.
Попробуйте повторить позже
Подсказка 1
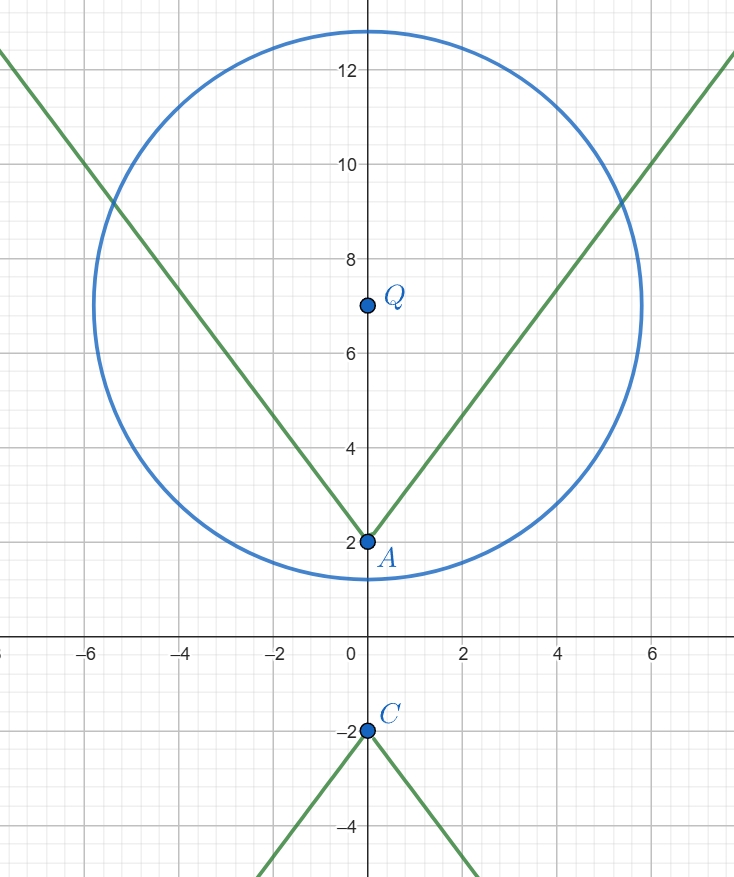
Для начала построим график первого уравнения: оно не зависит от параметра а. Заметим, что график этот симметричен относительно обеих координатных осей, это можно использовать при его построении!
Подсказка 2
Второе уравнение включает в себя х² и у² и не включает перекрёстных слагаемых, это наводит на мысль о том, что надо попытаться получить из него уравнение окружности!
Подсказка 3
Пункт (а). Нужно получить нечётное число решений, а построение симметрично относительно оси у. Как тогда должна располагаться окружность?
Подсказка 4
Пункт (б). Если предположить, что окружность пересекает нижний "уголок", то и верхний она тоже пересекает и решений уже больше двух. Поэтому подходящие значения а нужно искать в том диапазоне, когда окружность пересекается только с верхним "уголком"!
Заметим, что первое уравнение при замене на
или
на
не меняется. Тогда график этого уравнения симметричен
относительно обеих координатных осей. При
и
это уравнение имеет вид
— луч с началом в точке
и
угловым коэффициентом
Используем симметрию и строим график этого уравнения, получаем два угла: с вершиной в точке
и с
вершиной в точке
и угловыми коэффициентами лучей
Во втором уравнении выделим полный квадрат Тогда это уравнение можно записать так:
Оно задает окружность с центром в точке и радиусом
(в случае
— это точка
).

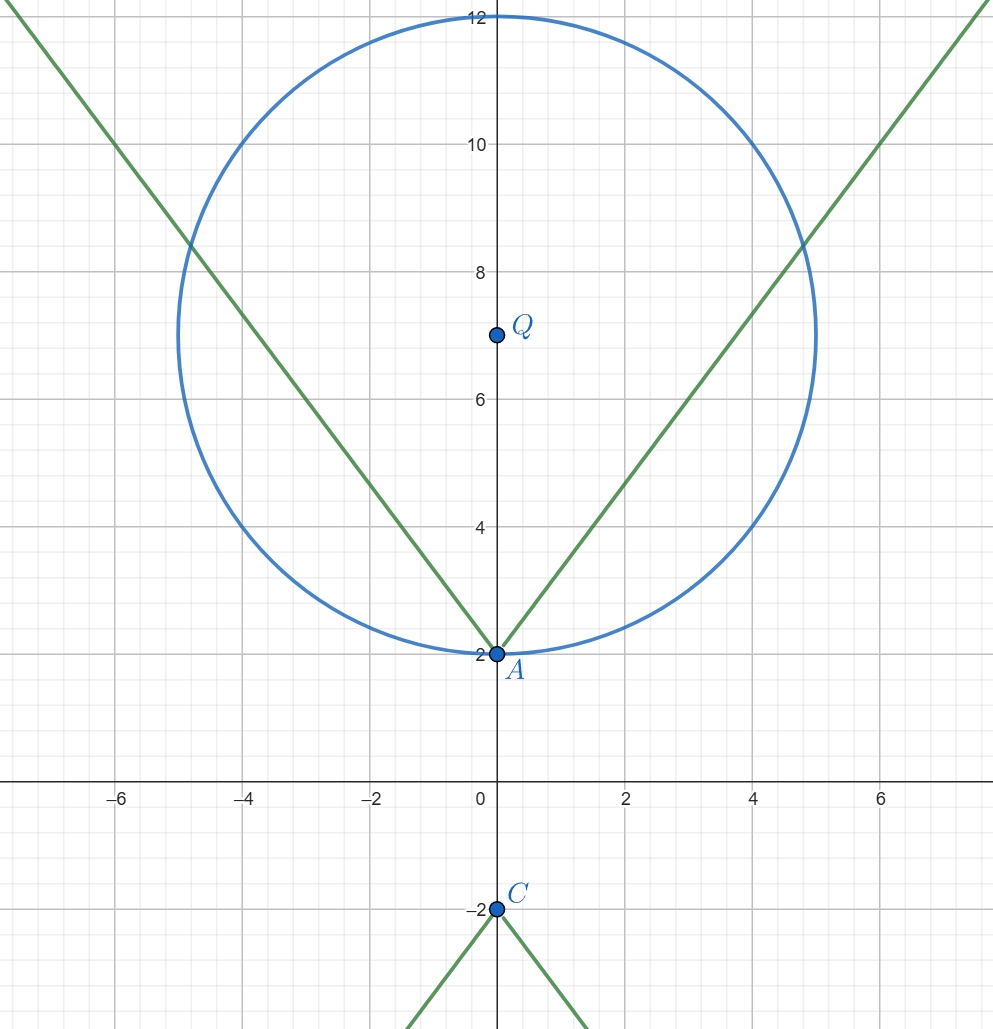
(a) Окружность и график первого уравнения симметричны относительно оси Тогда три решения возможны только в том
случае, когда одна из их общих точек лежит на оси этой оси. Это происходит, если радиус окружности равен отрезку
или отрезку
Так как
и
то получаем
или
Видно, что при этих
есть еще две общие точки со сторонами угла с вершиной в точке
поэтому любое
или
подходит.
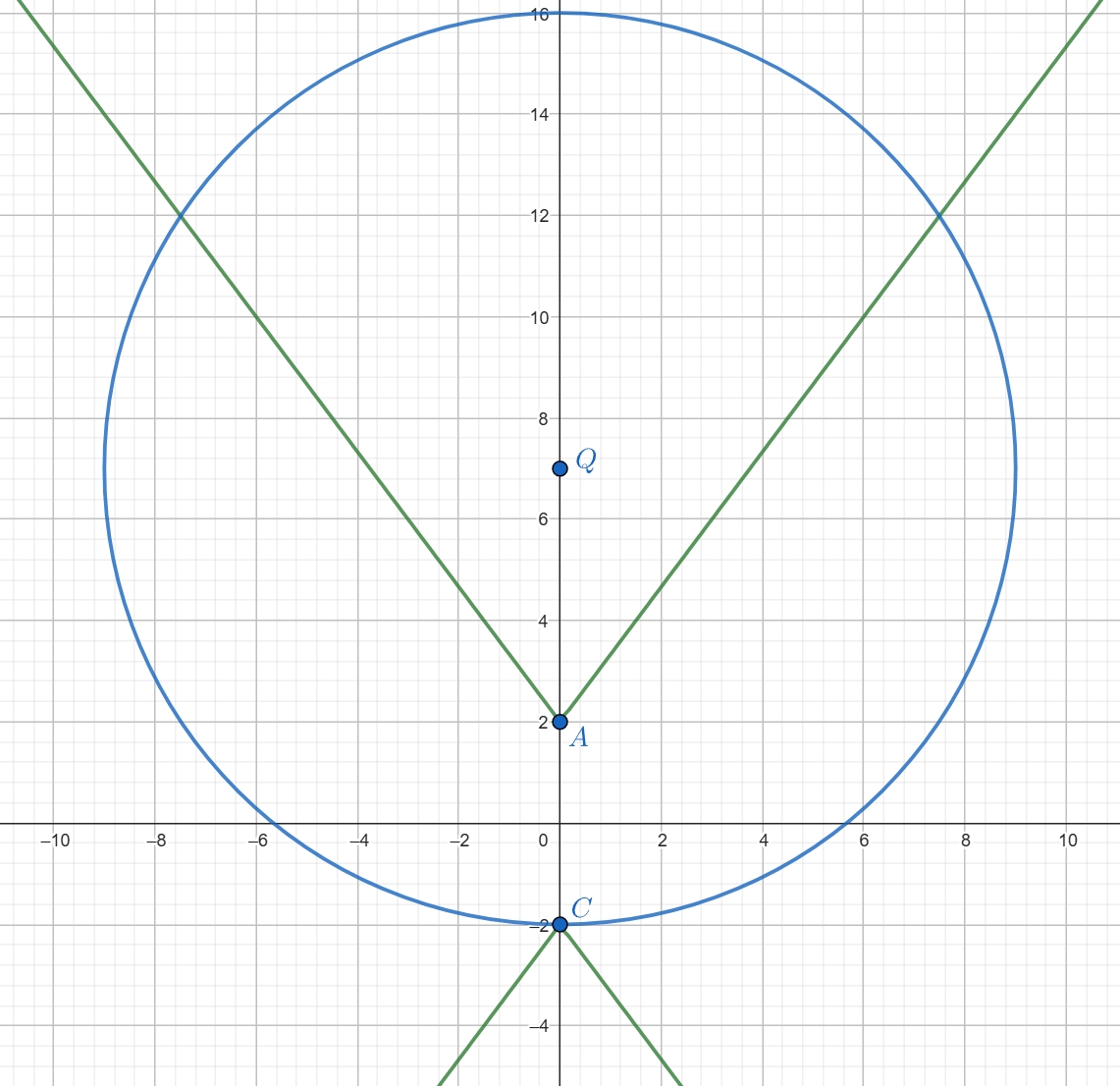
(b) Система дает два решения, если окружность касается угла с вершиной или имеет радиус, больший
но меньший
Мы уже знаем
и
так что осталось найти этот радиус (обозначим его
). Для этого опустим перпендикуляр
на сторону
угла с вершиной в точке
Пусть
— угол наклона прямой
(
Тогда
Так как
то
По теореме Пифагора для
получаем
Тогда

Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




