Графика. Отрезок, ромб, квадрат

Рассмотрим выражение как квадратный трёхчлен относительно Его дискриминант равен При дискриминант отрицателен, поэтому Если то т.е. при и при В итоге получаем, что выражение обращается в ноль в точке и положительно во всех остальных точках. Следовательно, первое неравенство системы равносильно совокупности Изобразим множество точек, удовлетворяющих этой совокупности, на координатной плоскости. Получаем все точки, лежащие на прямой и левее неё, точки на прямой и правее неё, а также точку

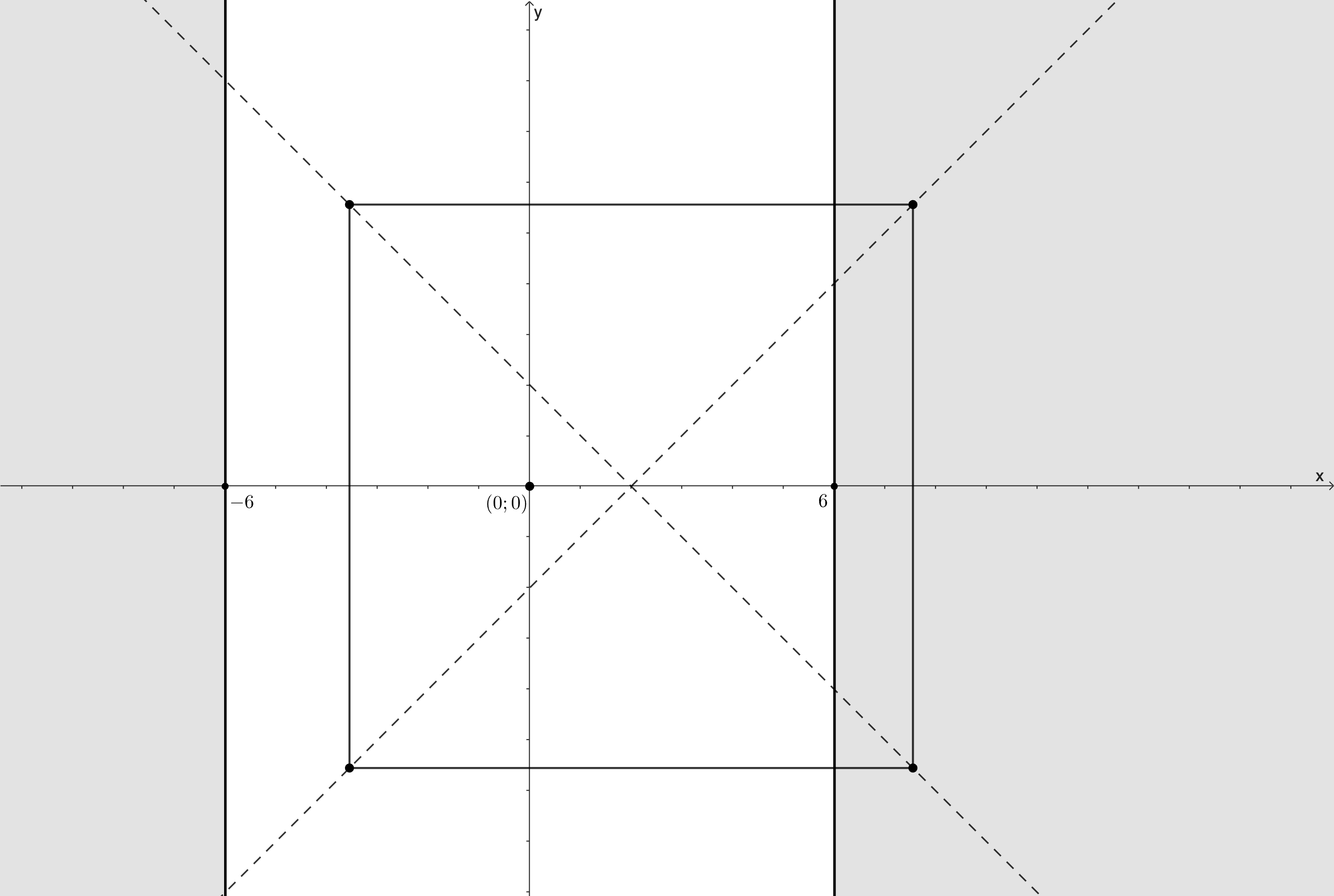
Перейдём ко второму неравенству. Проведём на координатной плоскости прямые и Они разбивают плоскость на 4 области, в каждой из которых знаки выражений под модулями постоянны. Рассматриваем 4 случая. Если и то неравенство принимает вид Аналогично, если и то . Если и то Если и то Окончательно получаем, что при неравенство задаёт точку при квадрат с центром в точке и стороной а при пустое множество.

Очевидно, при система не имеет решений. При для того, чтобы было единственное решение, нужно, чтобы точка попадала в квадрат, но чтобы квадрат не пересекал прямую откуда следует, что т.e.