Графика в xOa (параметр как вторая неизвестная)
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет решения. Укажите эти решения при найденных значениях параметра
Источники:
Подсказка 1
С тригонометрическими функциями работать неприятно, а в рамках таких нетривиальных равенств даже больно. Давайте замену x = 5cos t, y = 5sin t. Чтобы замена была равносильной, добавим в систему третьей уравнение x²+y²=25.
Подсказка 2
Давайте обратим внимание на второе равенство. Предлагается рассмотреть три случая: x < 0, 0 < x < 4, 4 < x. В каждом из этих случаев второе уравнение превращается в нечто простое.
Подсказка 3
В каждой в третье уравнение можно вместо y подставить его выражение через a и изобразить область первого неравенства и третьего равенства в осях xa. Дальше останется аккуратно понять, при каких a будут решения.
Сделаем следующие замены:
Имеем
Система распадается на совокупность трёх систем:
В системе координат изобразим решение системы
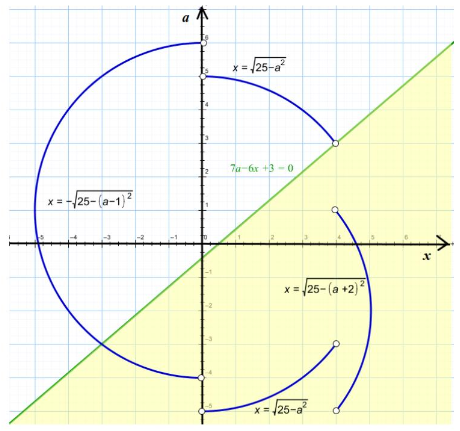
Имеем решение
Тогда
Откуда получается, что
При записи же ответа через нужно учитывать знаки
, т.е.
при
а при имеем
Имеем решение
при
. Тогда
Откуда получается, что
или
3) Имеем решение при
. Тогда
Откуда получается, что
или
при
имеем
при
имеем
при
имеем
при
имеем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




