Тема . Задачи с параметром

Графика в xOa (параметр как вторая неизвестная)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачу:

Ошибка.
Попробуйте повторить позже

Задача 1#127231

Найдите все значения параметра $a,$ при которых система

{ |x− a|+|y− a|+ |a− x+ 1|+|a− y +1|≤ 2 y+2||x2− 2x− 3||= 6

имеет единственное решение.

Источники: ШВБ - 2025, 10.4 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

Попробуйте заметить похожие выражения в левой части верхнего неравенства.

Подсказка 2

Что можно сказать о |t - a| + |a - t + 1|?

Подсказка 3

Докажите, что данное выражение всегда больше либо равно 1.

Подсказка 4

При каких t достигается равенство?

Подсказка 5

При t ∈ [a; a+1] данное выражение равняется 1. Заметим, что в исходном неравенстве 2 таких выражения.

Подсказка 6

Изобразите решения в координатах Oax и поймите, какие точки нам интересны.

Показать ответ и решение

Перегруппируем слагаемые верхнего неравенства:

|x − a|+ |a− x+ 1|+ |y − a|+ |a− y+ 1|≤ 2

Рассмотрим следующее выражение:

|t− a|+ |a− t+ 1|

Докажем, что оно больше либо равно единицы для любых $a$ и $t:$

|t− a|+ |a− t+1|≥ 1

Пусть $t<a :$

−t+a +a− t+ 1≥ 1

t≤a

Пусть $a≤ t≤a +1:$

t− a+ a− t+ 1≥ 1

1≥ 1

Пусть $t>a+ 1:$

t− a− a+t− 1≥ 1

t≥ a+ 1

Итого получаем, что $t ∈(−∞;+ ∞)$ и от значения $a$ ничего не зависит. Кроме того, равенство достигается при $t∈[a;a +1].$ Тогда

|x − a|+ |a− x+ 1|+ |y − a|+ |a− y+ 1|≥ 2

По условию,

|x − a|+ |a− x+ 1|+ |y − a|+ |a− y+ 1|≤ 2

Тогда верхнее неравенство из системы превращается в равенство. Оно будет верно, только если

|x − a|+ |a− x+ 1|= 1

|y − a|+ |a− y+ 1|= 1

Данные равенства выполняются, если $x,y ∈ [a;a+ 1].$

Перепишем исходную систему:

(| a ≤x ≤a +1 { a ≤y ≤a+ 1 |( y =6− 2|x2− 2x− 3|

{ a ≤x ≤a +1 a ≤6− 2|x2− 2x− 3|≤ a+ 1

Изобразим решения неравенств системы в координатах $Oax.$ Для первого неравенства получим полосу, заключенную между двумя прямыми $a= x$ и $a= x− 1.$ Решение второго неравенства будет множество точек, лежащих между двумя кривыми $a= 6− 2|(x− 1)2− 4|$ и $a= 5− 2|(x − 1)2− 4|.$

$PIC$

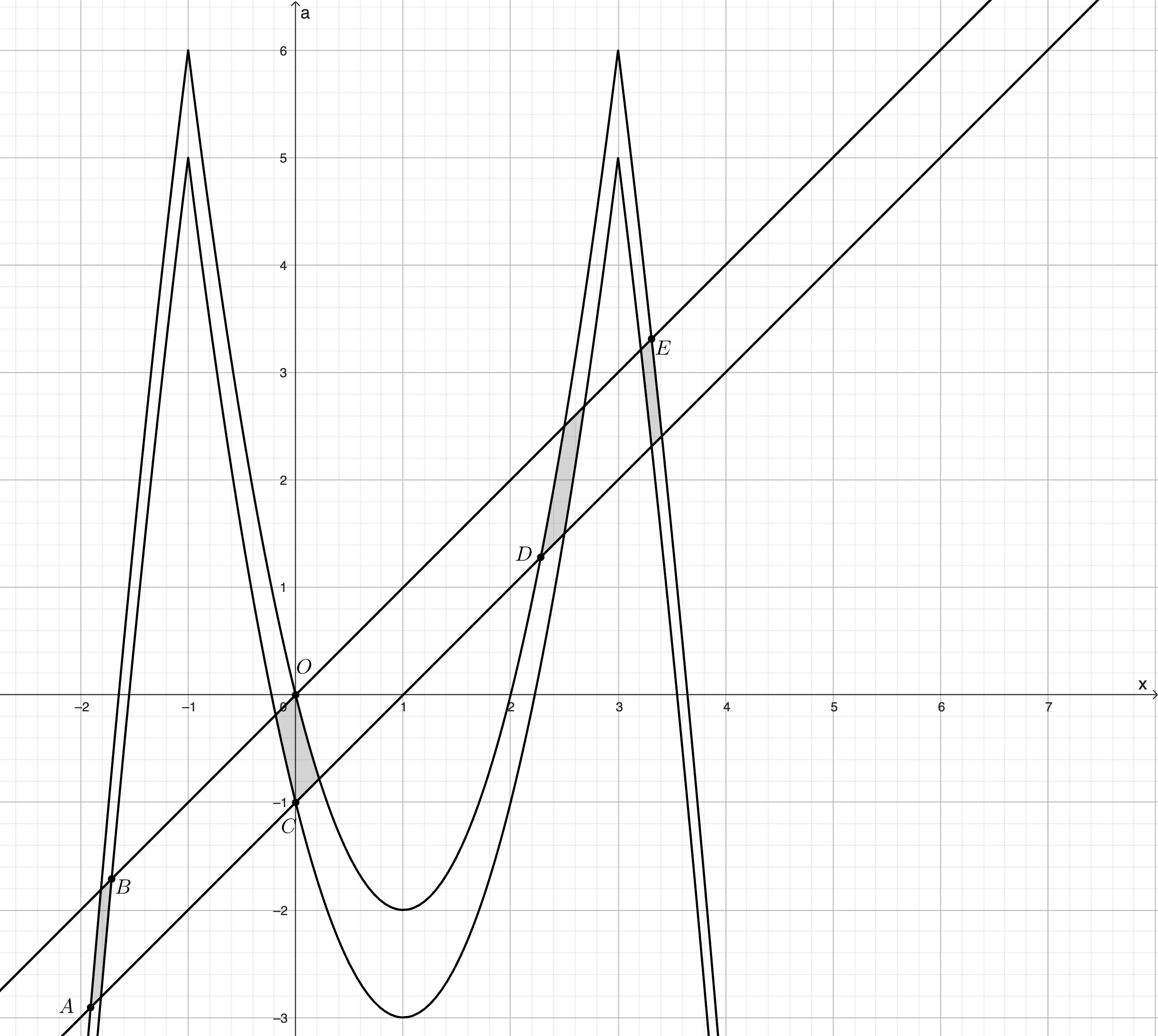
Решение системы будет единственным в тех случаях, когда прямая, параллельная оси $Ox,$ пересекает множество решений системы в одной точке. Подходящими точками являются $A,B,C,D,O,E.$ Найдем точки пересечения прямых $a= x$ и $a= x− 1$ с кривыми $a =6− 2|(x− 1)2− 4|$ и $a =5 − 2|(x− 1)2 − 4|.$

{ a= 6− 2|(x− 1)2− 4| a= x

Раскрываем модуль и подставляем $a :$

Если $x∈ (−∞; −1)∪(3;+ ∞):$

2x2− 3x − 12= 0

√--- x = 3±--105 4

Если $x∈ [−1;3]:$

2x2− 5x =0

x ={0;2,5}

Получим точки

( 3+ √105 3+√105) O = (0;0);E = ---4---;---4---

{ a= 5− 2|(x− 1)2− 4| a= x

Если $x∈ (−∞; −1)∪(3;+ ∞):$

2x2− 3x − 11= 0

√-- x= 3±--97 4

Если $x∈ [−1;3]:$

x2− 5x − 1 =0

√-- x= 5±--33 4

Получим точку

( 3−-√97 3−-√97) B = 4 ; 4

{ a= 6− 2|(x− 1)2− 4| a= x− 1

Если $x∈ (−∞; −1)∪(3;+ ∞):$

2x2− 3x − 13= 0

3± √113- x = ---4---

Если $x∈ [−1;3]:$

2x2− 5x+ 1= 0

5± √17 x= ---4--

Получим точки

( √--- √---) ( √ -- √--) A = 3−--113;−1−--113 ;D = 5-+--17;1+--17 4 4 4 4

{ 2 a= 5− 2|(x− 1) − 4| a= x− 1

Если $x∈ (−∞; −1)∪(3;+ ∞):$

2x2− 3x − 12= 0

√--- x = 3±--105- 4

Если $x∈ [−1;3]:$

2x2− 5x =0

x ={0;2,5}

Получим точку

C = (0;−1)

Мы получили все подходящие нам точки $A,B,C,D,O,E.$ Их координаты по $x$ равны $a$ или $a+1$ (в зависимоcти от того, с какой прямой пересечение). Тогда

{ −1− √113 3− √97 1+ √17 3+ √105} a∈ ----4---;--4---;−1;0;---4--;---4---

Ответ:

$−-1−-√113 4 ;$ $3−-√97 4 ;$ $− 1;$ $0;$ $1+-√17 4 ;$ $3+-√105 4$

Нужна консультация? Задайте нам вопрос в чате.

Специальные программы

Все специальные программы

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

Программа
лояльности v2.0

Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!

Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение

Налоговые вычеты

Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!

Графика в xOa (параметр как вторая неизвестная)

Специальные программы

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программалояльности v2.0

Крути рулеткуи выигрывай призы!

Бесплатное онлайн-обучение

Налоговые вычеты

Специальное предложениедля учителей

Вернём деньги за курсза твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ

Программа
лояльности v2.0

Крути рулетку
и выигрывай призы!

Специальное предложение
для учителей

Вернём деньги за курс
за твою сотку на ЕГЭ