Экстремальные задачи в планиметрии
Ошибка.
Попробуйте повторить позже
В треугольник , в котором сумма сторон
и
в
раз больше стороны
, вписана окружность, касающаяся сторон
и
в точках
и
соответственно. Отношение площади треугольника
к площади треугольника
равно
.
Найдите при данных условиях:
а) наименьшее значение ;
б) все возможные значения .
Источники:
Подсказка 1!
Для начала посмотрим на пункт а. Заметим, что у нас тут есть какие-то отрезки касательных, может быть мы можем выразить их через стороны треугольника как-то..?
Подсказка 2!
Верно! MC = NC = Полупериметр - c! А еще в треугольнике MNC две равных стороны, которые мы можем так выразить. Тааааааак, а как бы нам теперь зная много сторон найти отношение площадей?
Подсказка 3!
В таких случаях мы пишем отношение площадей через формулу двух сторон и угла между ними! Было бы здорово, если бы угол был общий, попробуйте угол С?
Подсказка 4!
А теперь в получившейся формуле осталось прийти к минимуму! (a+b) и ab, что-то знакомое..
Подсказка 5!
Хм, а пункт б? Раскроем скобки в последнем выражении для отношения площадей и сделаем замену t = a/b! Тогда что будет в скобках? В точности t+1/t+2. Осталось найти возможные значения t!
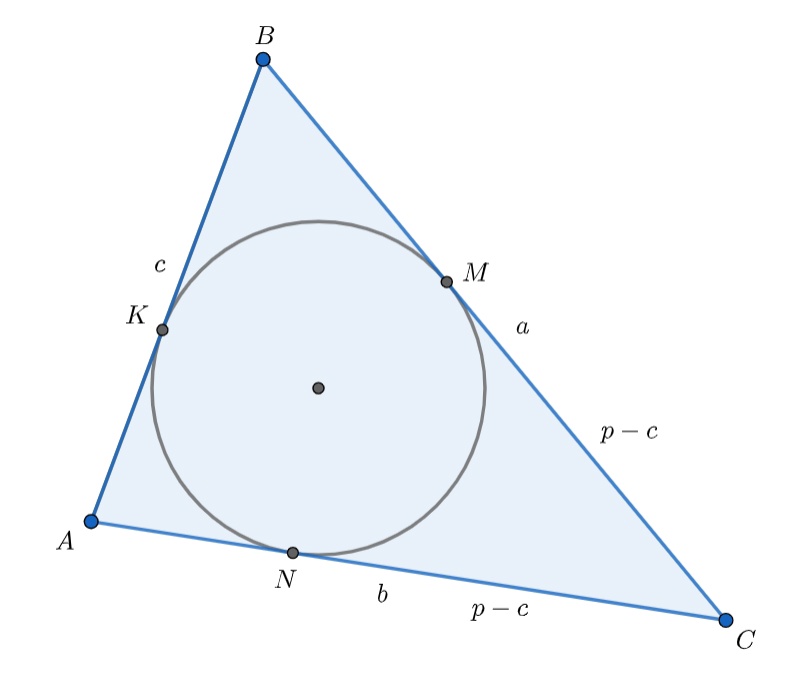
а) По формуле отрезков касательных для вписанной окружности имеем — стороны
треугольника, отсюда
Используем неравенство о средних (знак равно достигается, только в случае
), то
.
б) Перепишем отношение площадей в следующем виде:
где . По неравенству треугольника
. Учитывая то, что
последние неравенства
равносильны
. Отсюда
. Функция
монотонно убывает на
и возрастает на
, она
симметрична относительно
, откуда
. В итоге находим множество значений
на
отрезке
. Любое промежуточное значение можно задать выбором
и
.
а)
б)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




