Экстремальные задачи в планиметрии

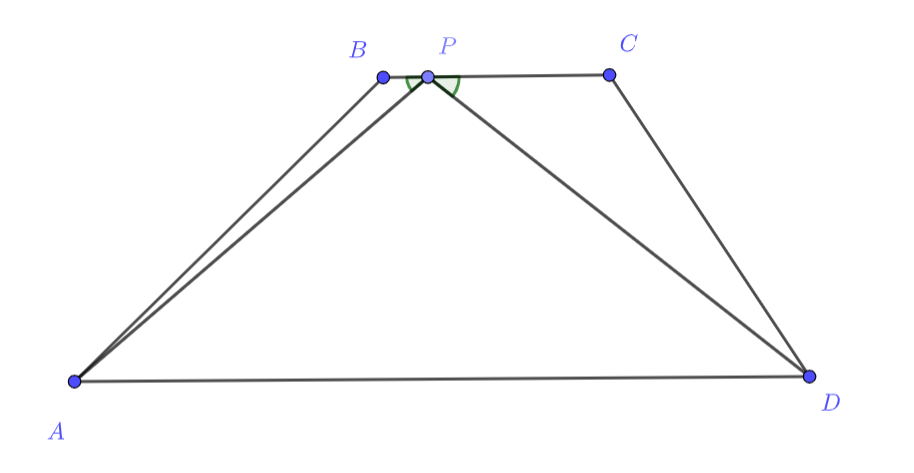
Первое решение.

Воспользуемся следующим утверждением, которое наиболее известно как «принцип наименьшего времени Ферма» в физике:

Для данных точек и данной прямой из всех точек сумма будет минимальной, когда углы между прямыми и и и будут равны.

Тогда для искомой точки на прямой должно выполняться равенство (точки и - где-то «далеко» на прямой . Поскольку , то

т.е. треугольник - равнобедренный. Значит, нам достаточно найти периметр равнобедренного треугольника , где - точка на прямой .

По теореме Пифагора этот периметр равен

где - расстояние между прямыми и , т.е. высота трапеции.

Найти высоту трапеции можно разными способами. Например, проведём через точку , прямую, параллельную , до пересечения с основанием в точке . Тогда искомая высота - это высота из вершины в треугольнике . Поскольку параллелограмм, то , .

Итого, нам достаточно найти длину высоты на сторону длины 7 в треугольнике со сторонами 5 , . По формуле площади и формуле Герона имеем

откуда

и окончательный ответ .

Второе решение.

Также, как и в первом решении, найдём высоту трапеции. Покажем здесь, как можно это было сделать по-другому. Опустим высоты и трапеции. Обозначим их длины через , длину отрезка обозначим через . Поскольку , для получим . Из прямоугольных треугольников и по теореме Пифагора получим и

Подставив в эти равенства известные длины, получим систему уравнений

Вычитая из первого равенства второе, получим , откуда . Тогда .

Рассмотрим треугольник . Обозначим , тогда (здесь и далее все расстояния со знаком, т.е. могут быть отрицательные). Опустим высоту . Тогда треугольник прямоугольный и по теореме Пифагора

Аналогично, из прямоугольного треугольника

Тогда периметр треугольника равен

Найдём производную этой функции:

Из уравнения получаем

откуда . Несложно видеть, что именно точка минимума, откуда минимальный периметр равен .