Экстремальные задачи в планиметрии

Из условия следует равенство дуг и значит, биссектриса угла пересекает окружность в точке . По лемме о трезубце

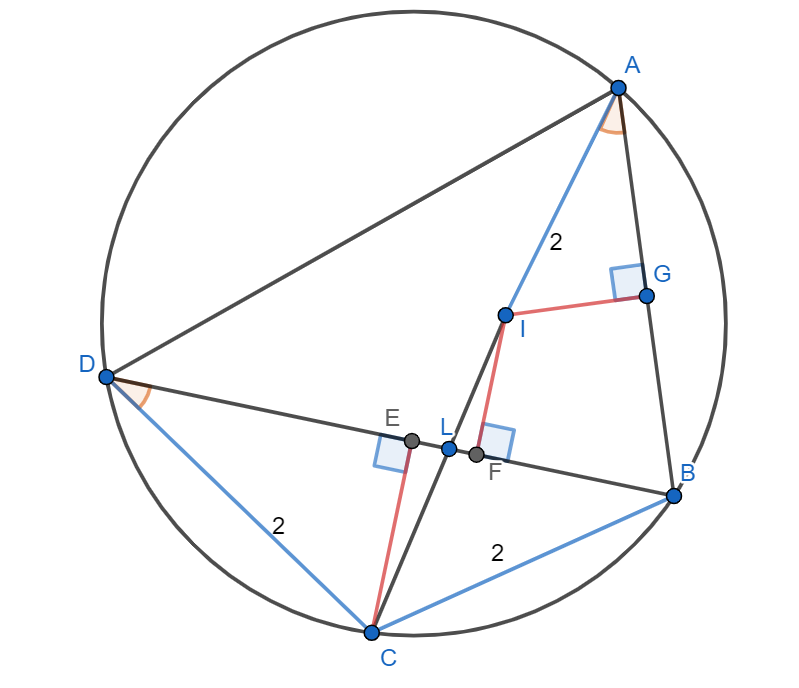
Пусть – основания перпендикуляров, опущенных из точек и на и соответственно, тогда из равенства прямоугольных треугольников и по острому углу (равные вписанные углы) и гипотенузе (из условия) следует, что Перпендикуляр к диагонали также равен (это радиусы вписанной окружности треугольника поэтому пересекает отрезок в его середине из равенства прямоугольных треугольников и по катету и острому углу (вертикальные).

Таким образом, По теореме о произведении отрезков хорд Пусть тогда А по неравенству о средних

Наименьшее значение достигается при Построим равнобедренный треугольник с боковыми сторонами и высотой Тогда Продлим за точку на длину получим точку Отметим — центр вписанной окружности треугольника Тогда из леммы о трезубце получим а значит, и построенная картинка удовлетворяет условию.