Экстремальные задачи в планиметрии
Ошибка.
Попробуйте повторить позже
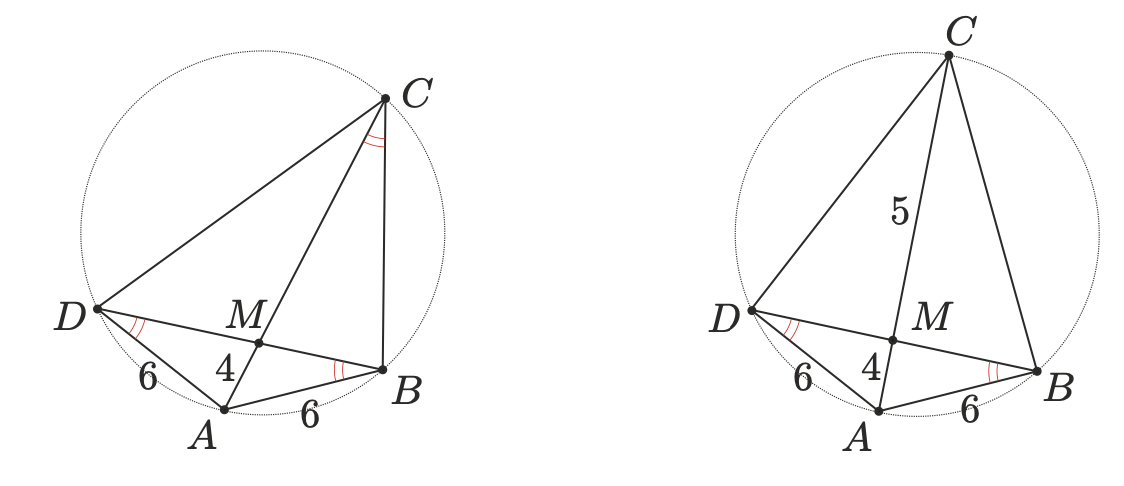
В окружность с центром вписан четырехугольник
, диагонали
и
которого пересекаются в точке
, причем
. Определите, какой может быть наименьшая длина диагонали
, если известно, что стороны
и
равноудалены от точки
.
Источники:
Подсказка 1
Какой вывод можно сделать из равноудаленности AB и AD от точки O?
Подсказка 2
Они равны! А что вытекает из равенства хорд в окружности?
Подсказка 3
Углы ACD, ADB, ABD равны! Не возникло ли где у нас подобия? Быть может, можно посчитать еще какие-то отрезки?
Подсказка 4
Треугольники ABM и ACB подобны! Отсюда можно посчитать какие-нибудь отрезки. Теперь попробуем подступиться к отрезкам на DB. Быть может, попробуем их выразить при помощи свойства отрезков на пересекающихся хордах?
Подсказка 5
DM * MB = CM * MA = 5*4, что есть DM = 5x, MB = 4/x. Осталось лишь минимизировать сумму ;)
Из равноудалённости сторон и
от точки
вытекает их равенство. Следовательно равны углы
.
Таким образом, треугольники
и
подобны. Откуда
, т.e.
, а следовательно,
. Так как
, то
Следовательно,
применяя . Остаётся заметить, что данный случай реализуется, когда
проходит через центр окружности.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




