6.01 Определение результатов работы простейших алгоритмов управления исполнителями

Идея решения:

Для моделирования движения Черепахи используем модуль turtle. Сначала реализуем первую фигуру через цикл с двумя повторами. Затем поднимаем хвост, смещаемся на нужное расстояние, поворачиваем, и опускаем хвост для построения второй фигуры (тоже через цикл). Чтобы было удобно анализировать пересечение, используем масштабирование (например, умножаем все отрезки на 12). После построения обеих фигур перебираем точки с целочисленными координатами в заданном диапазоне, отмечаем их на экране и в дальнейшем можно посчитать количество точек, попавших внутрь объединения.

Решение:

# Подключаем модуль для исполнителя Черепаха
from turtle import *

# Масштаб для увеличения фигур
m = 12

# Отключаем анимацию для быстрого выполнения
tracer(0)

# Опускаем хвост, начинаем рисовать
pd()

# Направляем голову вверх (по оси y)
left(90)

# Первая фигура, цикл из двух повторов
for i in range(2):
    # Двигаемся вперёд на 14 единиц
    forward(14 * m)
    # Поворачиваем налево на 270°
    left(270)
    # Двигаемся назад на 12 единиц
    backward(12 * m)
    # Поворачиваем направо на 90°
    right(90)

# Поднимаем хвост, чтобы перемещаться без рисования
pu()

# Смещаемся вперёд на 9 единиц
forward(9 * m)
# Поворачиваем направо на 90°
right(90)
# Смещаемся вперёд на 7 единиц
backward(7 * m)
# Поворачиваем налево на 90°
left(90)

# Опускаем хвост для рисования второй фигуры
pd()

# Вторая фигура, цикл из двух повторов
                                                                                                  
                                                                                                  
for i in range(2):
    # Двигаемся вперёд на 13 единиц
    forward(13 * m)
    # Поворачиваем направо на 90°
    right(90)
    # Двигаемся вперёд на 6 единиц
    forward(6 * m)
    # Поворачиваем направо на 90°
    right(90)

# Поднимаем хвост для проставления точек
pu()

# Перебираем точки с целыми координатами
for x in range(-50, 50):
    for y in range(-50, 50):
        # Переходим в точку (x,y)
        goto(x * m, y * m)
        # Ставим точку
        dot(3)

# Завершаем выполнение графики
done()

Необходимо посчитать количество точек внутри объединения фигур, включая точки на границах пересечения:

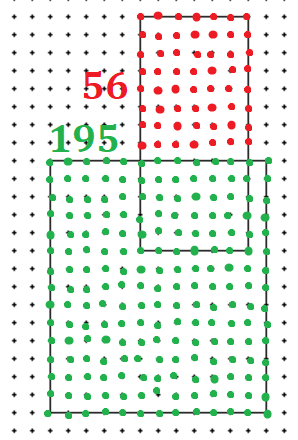
Получаем 56 красных точек и 195 зеленых, общее количество равно: