Окружность Эйлера
Ошибка.
Попробуйте повторить позже
Найдите угол треугольника
если на его окружности девяти точек лежит середина отрезка
где
— центр описанной
окружности.
Подсказка 1
Для начала, нужно определить где находится центр окружности Эйлера. Самый легкий способ определения - середина OH, Н - ортоцентр. А значит нужно отметить ортоцентр. Если середина BO (пусть - Х) лежит на окружности, это значит, что (пусть O_e - центр окружности Эйлера) XO_e - радиус окружности Эйлера. Но при этом, в силу гомотетии, радиус описанной окружности в два раза больше чем радиус окружности Эйлера. Что тогда это значит для треугольника BOO_e?
Подсказка 2
Верно, медиана XO_e в два раза больше стороны BO. Значит угол BO_eO=90 градусов. А что это значит для треугольника HBO? Как выйти из этого на угол B?
Подсказка 3
Это значит, что треугольник HBO-равнобедренный, так как BO_e-высота и медиана. Значит, BH=BO и мы вышли на что-то явное и понятное(более того, у вас была буквально такая задача в прошлом дз). Ну хорошо, BO - радиус описанной окружности. А как через радиус выразить BH?
Подсказка 4
Вспомним свойство ортоцентра! Расстояние от центра окружности до середины стороны AC равно половине BH. При этом, из прямоугольного треугольника, оно равно R*cos(B). Значит, BH=2R*cos(B). Мы выразили BH через радиус, значит , ничего не мешает нам найти угол B!
Пусть — центр окружности Эйлера,
— середина
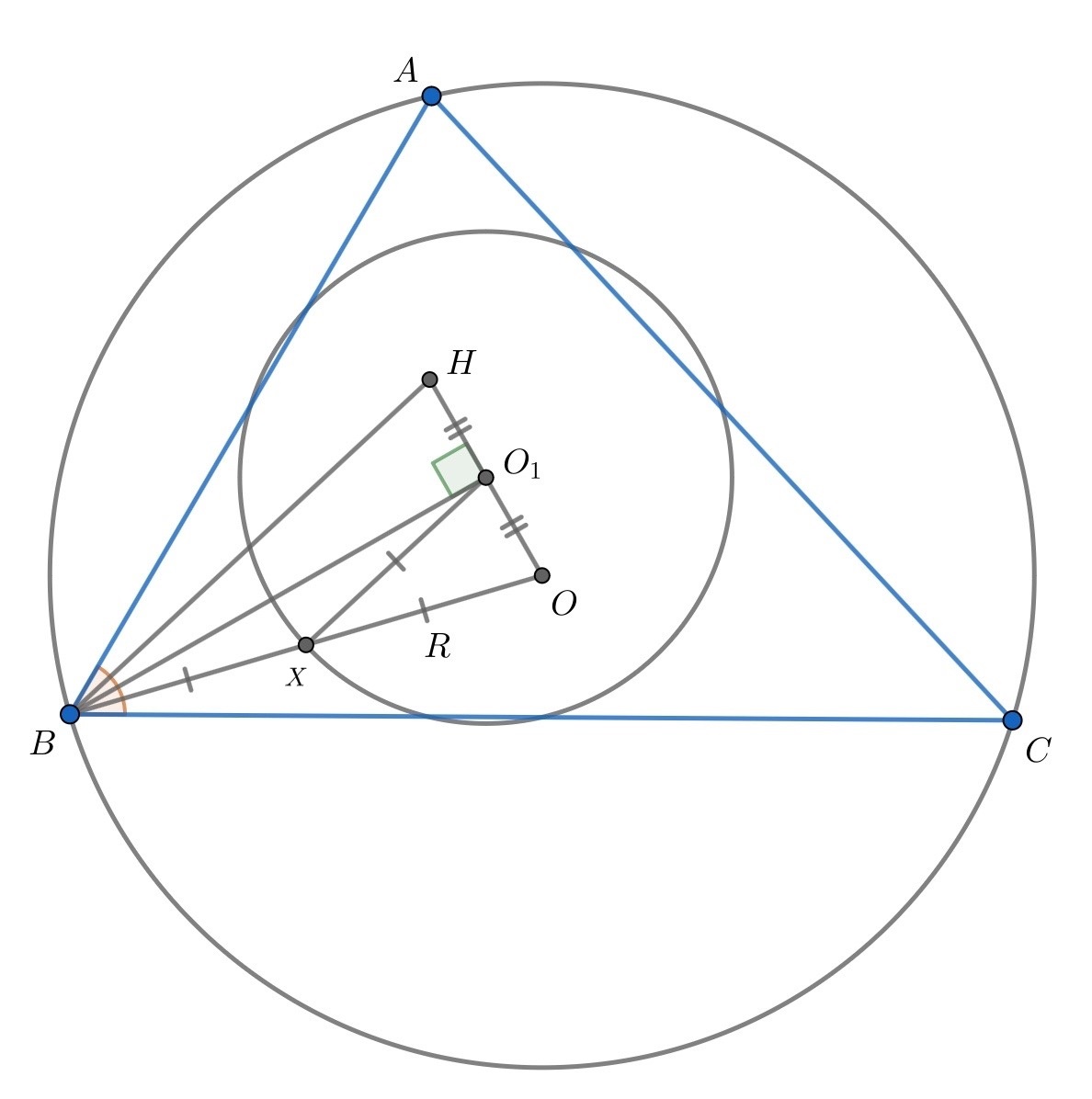
Заметим, что в треугольнике медиана
равна половине стороны, к которой она проведена (потому что радиус окружности
Эйлера равен половине радиуса описанной окружности), откуда
Таким образом, — высота и медиана в
значит он равнобедренный, то есть
По свойству ортоцентра . Тогда из
следует:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




