Окружность Эйлера
Ошибка.
Попробуйте повторить позже
Докажите, что описанная окружность треугольника является окружностью девяти точек для треугольника, образованного центрами
вневписанных окружностей треугольника
Подсказка 1
Через какие вообще точки проходит окружность Эйлера? Через основания высот и тройки середин отрезков. Если предполагать, что задача не гроб , и что вершины треугольника ABC - это какие-то из этих троек точек, то какой бы тройкой они могли быть?
Подсказка 2
Серединами сторон точно нет, так как расстояние от вершины треугольника до центров соответствующих ей вневписанных окружностей, очевидно, не всегда равно. Значит, тройки, связанные с серединами чего-то отпадают. Остаются только высоты. Во-первых, что можно сказать про прямую, которая проходит через два центра вневписанных окружностей?
Подсказка 3
Верно, она проходит через одну из вершин треугольника, так как центры вневписанных окружностей лежат на биссектрисах внешних углов, а углы вертикальные. Если против каждой вершины треугольника Х лежит вневписанная окружность с центром O_x, то чему равен, к примеру, угол O_b A O_a?
Подсказка 4
Верно, так как это угол между внешней биссектрисой A O_b и внутренней A O_a, то угол O_b A O_a равен 90 градусам. То есть,
чевиана O_a A в треугольнике O_a O_b O_c - это высота. Но что нам тогда мешает провести аналогичные рассуждения относительно других таких чевиан? А разве мы еще не решили задачу?
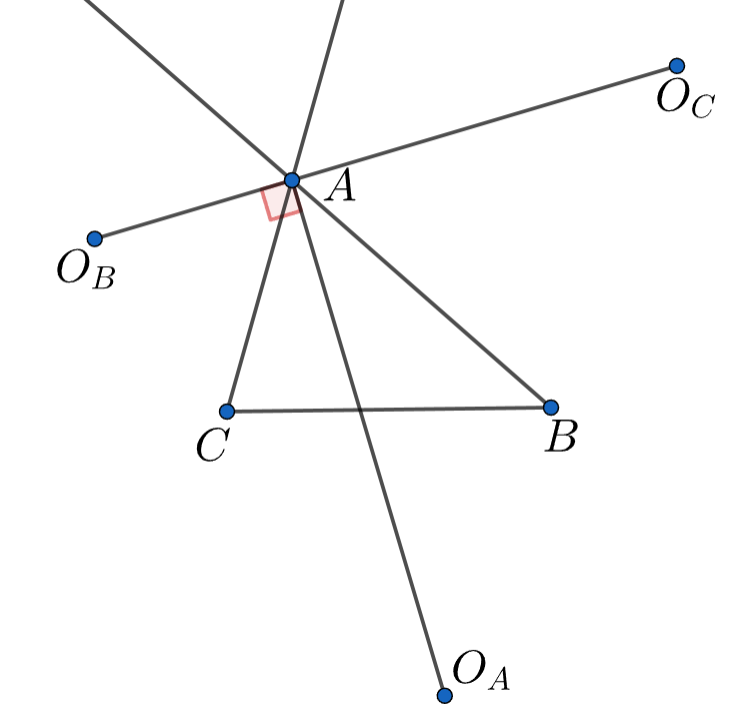
Пусть — центр вневписанной окружности напротив точки
Остальные центры определим аналогично.
и
— биссектрисы
внешнего угла
при вершине
а значит, точки
лежат на одной прямой.
Рассмотрим биссектрису угла треугольника
С одной стороны, она перпендикулярна
потому что
биссектрисы смежных углов перпендикулярны. С другой стороны, она проходит через
Таким образом, она является
высотой
а точка
— её основанием. Аналогично,
и
являются основаниями соответствующих высот в
Теперь требуемое очевидно из определения окружности Эйлера, ведь исходный треугольник является ортотреугольником для треугольника с вершинами в центрах вневписанных окружностей.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




