Окружность Эйлера
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность. Из середины каждого отрезка, соединяющего две точки касания, проводится перпендикуляр к
противолежащей стороне. Докажите, что эти перпендикуляры пересекаются в одной точке.
Подсказка 1
Иногда удобнее работать не с самой задачей, а с задачей, которая тождественна данной, но при этом формулируется легче и понятнее. Переформируем задачу так:
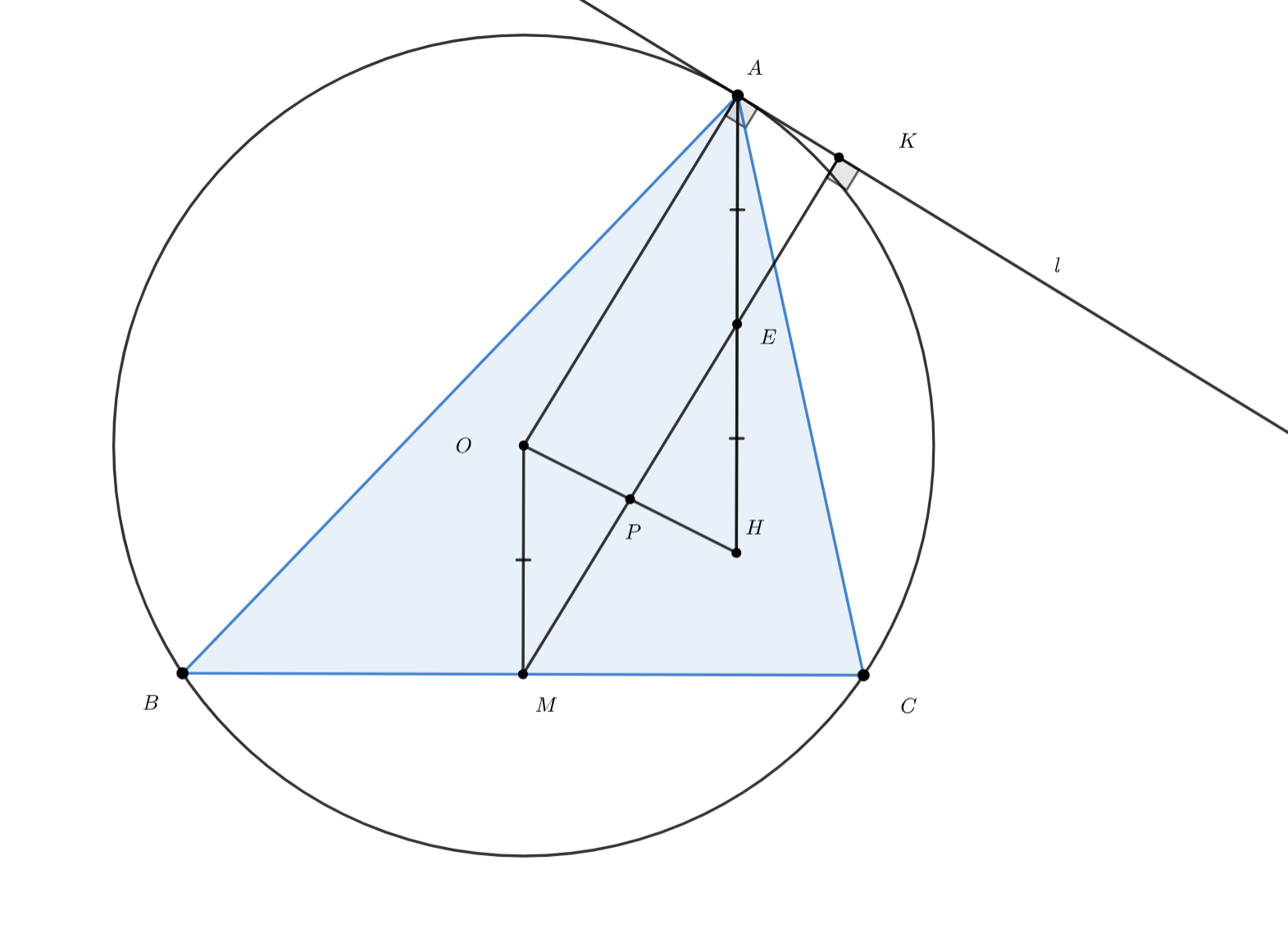
Рассмотрим треугольник ABC и его описанную окружность. Проведём к ней касательную l в точке A , а из середины M стороны BC проведём прямую a , перпендикулярную l. Аналогично определим прямые b и c . Требуется доказать, что прямые a , b и c пересекаются в одной точке.
Попробуйте теперь как-то связать эту задачу с темой веба.
Подсказка 2
Если мы хотим как-то связать данную задачу с темой веба, то, поскольку точка О - центр описанной окружности, уже отмечена, то остается лишь отметить точку Н. Если основание высоты из точки M - середины стороны BC - на прямую l - это К, то как связаны MK и AO? А что дает эта связь? Какие отрезки тогда выходят равными?
Подсказка 3
В силу того, что ОМ и AH параллельны, а также, так как МК и АО параллельны, поскольку каждый из них перпендикулярен l, MOAE - параллелограмм(Е-пересечение AH и МК). Что тогда можно сказать, используя свойство ортоцентра, которое связывает OM и AH?
Подсказка 4
Поскольку 2OM=AH, и при этом OM=AE, по свойству параллелограмма, то OM=EH. И при этом OM || EH. Значит MOEH-параллелограмм. А что это значит для нас, в рамках доказательства задачи? Что это нам дает?
Подсказка 5
Верно, диагонали точкой пересечения у MOEH делятся пополам. А значит МЕ пересекает отрезок OH(который задает прямую Эйлера) в середине. Ого! Так значит наша прямая MK проходит через середину OH, то есть через центр окружности Эйлера! Но что нам мешает доказать тоже самое относительно других прямых, которые являются высотами к касательным в вершинах треугольника? А кажется, мы решили задачу :)
Так как стороны исходного треугольника являются касательными к описанной окружности треугольника, образованного точками касания, то задачу удобно переформулировать:
Рассмотрим треугольник и его описанную окружность. Проведём к ней касательную
в точке
а из середины
стороны
проведём прямую
перпендикулярную
Аналогично определим прямые
и
Требуется доказать, что прямые
и
пересекаются в одной точке.
Заметим, что так как они обе перпендикулярны к
Пусть
— ортоцентр треугольника
— середина
Из того, что
и соотношения
(свойство ортоцентра) следует, что
и
—
параллелограммы(их противолежащие стороны равны и параллельны). Значит,
то есть прямые
и
совпадают. Из
параллелограмма
получим, что
содержит середину
отрезка
Проведя аналогичные рассуждения,
получим, что прямые
и
также проходят через точку
Таким образом, прямые
и
пересекаются в одной
точке.
является центром окружности девяти точек треугольника
а
— один из её диаметров. Эти факты можно использовать в
заключительной части рассуждения.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




