Окружность Эйлера
Ошибка.
Попробуйте повторить позже
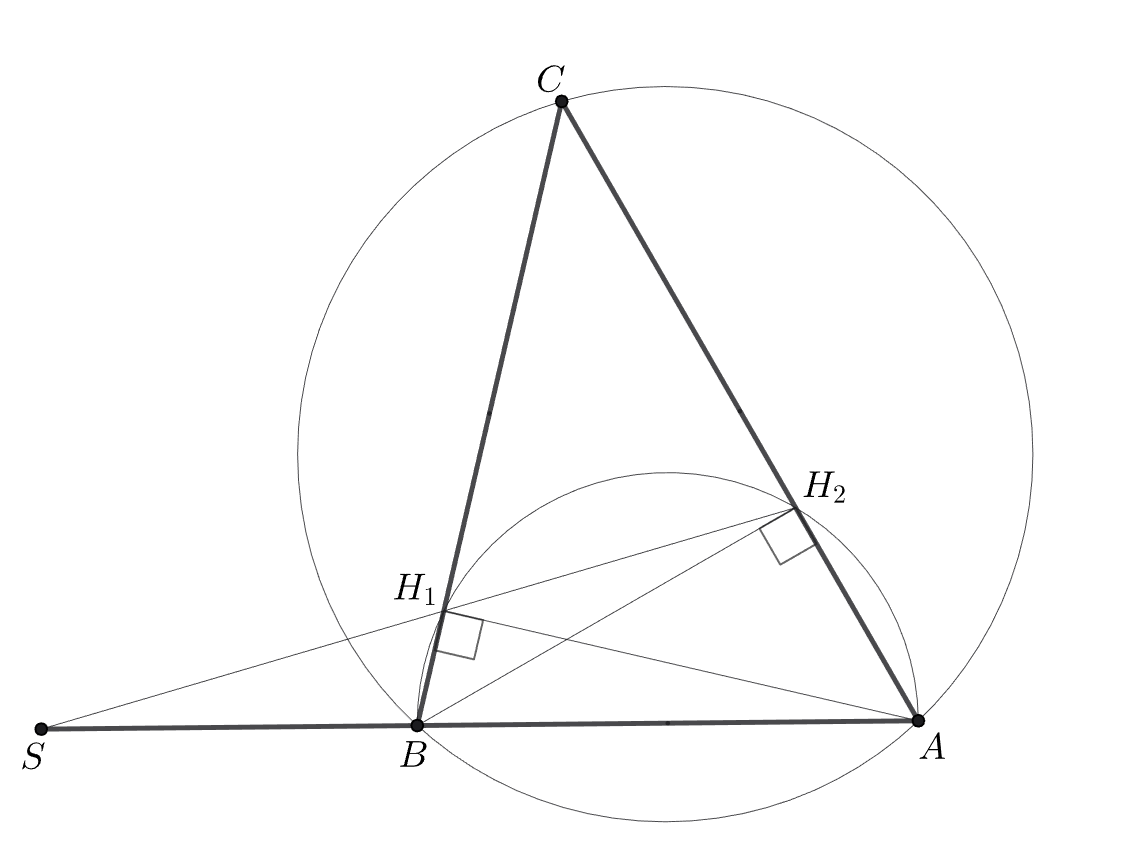
В треугольнике
и
— высоты; касательная к описанной окружности в точке
пересекает
в точке
а
касательная в точке
пересекает
в точке
и
— середины отрезков
и
Докажите, что
и
пересекаются в одной точке.
Подсказка 1
Нас просят доказать, что какие-то прямые пересекаются в одной точке) Причём две из этих прямых связаны с каким-то вписанным четырехугольником(который несложно найти на картинке)! На какой геометрический объект(или явление), связанный с окружностями(или вписанным четырехугольником) намекают нам три пересекающиеся прямые?
Подсказка 2
На радикальный центр! Попробуем найти окружности, для которых удобные нам прямые AB и H₁H₂ являются радикальными осями. Как можно связать T₁T₂ с этими окружностями?
Подсказка 3
AB - радикальная ось окружностей (ABC) и (ABH₁H₂). H₁H₂ - радикальная ось окружностей (ABH₁H₂) и окружности Эйлера. Тогда попробуем доказать, что T₁T₂ - радикальная ось окружности (ABC) и окружности Эйлера. Условие у нас симметрично для точек T₁ и T₂, поэтому можно доказать лишь для одной из них, что она находится на нужной нам радикальной оси. Какими условиями мы еще не пользовались?
Подсказка 4
Мы не пользовались касанием T₁A и окружности (ABC), а также тем, что T₁ - середина S₁A. Не совсем понятно, как связать окружность Эйлера с T₁ без каких-то дополнительных точек. Какие точки на окружности Эйлера можно использовать?
Подсказка 5
Точка T₁ - это середина отрезка, так что отметим B₀ и C₀, которые лежат на окружности Эйлера и докажем, что степень точки T₁ относительно окружностей (ABC) и окружности Эйлера одинакова. Посчитать степень точки T₁ относительно (ABC) не составит труда(в силу касания), а относительно окружности Эйлера она равна T₁B₀*T₁C₀. Осталось лишь доказать равенство (T₁A)² = T₁B₀*T₁C₀!
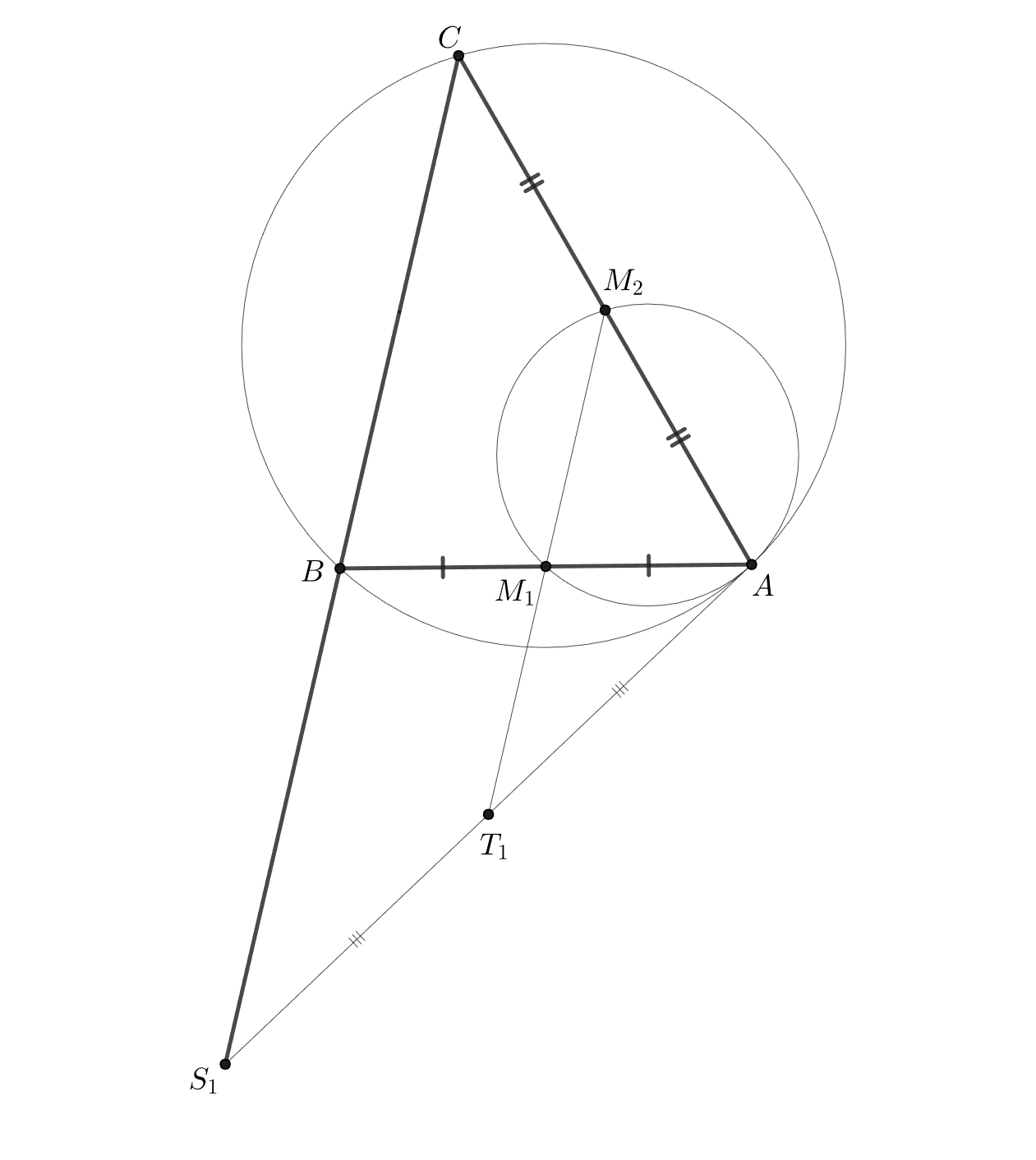
Пусть — точка пересечения прямых
и
— описанная окружность и окружность Эйлера треугольника
Докажем,
что точки
и
имеют равные степени точек относительно
и
и, следовательно, лежат на одной прямой — их радикальной
оси.
Действительно, точки лежат на окружности с диаметром
а значит,
С другой стороны, если — середины сторон
и
соответственно, то
поскольку окружность отличается от окружности
гомотетией с центром в точке
и коэффициентом
а значит,
касается последней. Аналогично, точка
имеет равные степени точек относительно указанных окружностей.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




