Окружность Эйлера

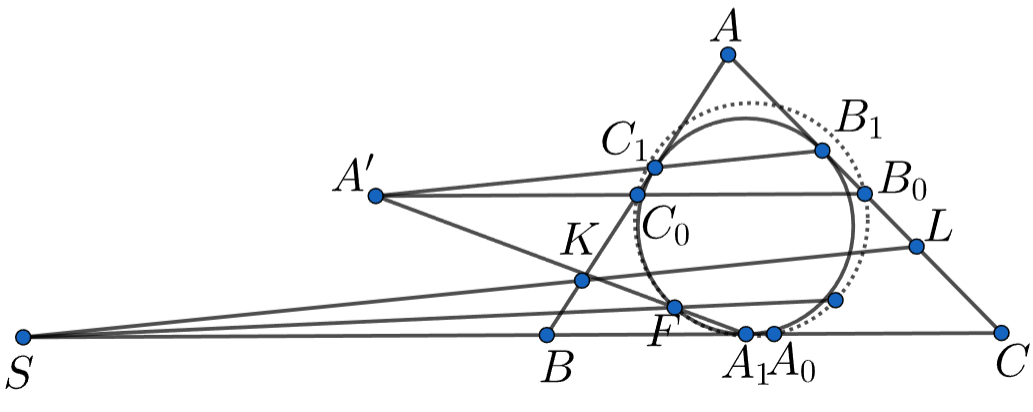
Докажем, что проходит через где — точка Фейербаха. Аналогично доказывается, что и проходят через и соответственно, откуда следует утверждение задачи.

Пусть и  – вписанная окружность и окружность Эйлера треугольника Сделаем гомотетию этих окружностей с коэффициентом и центром Обозначим их образы как и соответственно. проходит через и А касается так как по теореме Фейербаха касается и прямых и Пусть и  – соответствующие точки касания, а  – точка касания этих окружностей.

Если то и утверждение очевидно из симметрии.

Пусть Тогда докажем следующую лемму.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Пусть окружности и касаются внутренним образом в точке Из точек и окружности проведены соответственно касательные и к окружности Пусть Тогда прямая проходит через середину дуги окружности (если то  – середина дуги ).

Доказательство. Достаточно доказать, что — это биссектриса (внутренняя или внешняя — в зависимости от конфигурации) угла то есть, что

Применяя теорему Менелая к треугольнику, образованному прямыми и с секущей и используя равенство длин касательных к проведенных из одной точки, получаем:

Пусть и — вторые точки пересечения прямых и с При гомотетии с центром переводящей в точки и перейдут соответственно в и значит Поэтому Отсюда то есть что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Значит, наша прямая пересекает вторично в точке — середине дуги Касательная к проведенная в параллельна Пусть пересекает вторично в точке При гомотетии с центром переводящей в точка переходит в поэтому касательная к проведенная в также параллельна

Теперь сделаем обратную гомотетию. Точки и перейдут в и соответственно, точки и  – в и поэтому как точка пересечения и переходит в Точка переходит в точку так как касательная к проведенная через параллельна и переходит в Точка разумеется, переходит в значит прямая переходит в прямую Чтобы доказать, что точка лежит на достаточно показать, что лежит на а это выполнено по построению