18.04 Шахматные фигуры
Ошибка.
Попробуйте повторить позже
Квадрат разлинован на N N клеток (1 < N < 25). Исполнитель Ладья может перемещаться по клеткам, выполняя за
одно перемещение движение на любое количество клеток вправо или вниз. При попытке выхода за границу квадрата Ладья
разрушается. Перед каждым запуском Ладьи в каждой клетке квадрата лежит монета достоинством от -100 до
100. Посетив клетку, Ладья забирает монету с собой; это также относится к начальной и конечной клетке
маршрута Ладьи. Изначально Ладья стоит в левой верхней клетке. Конечной точкой является правая нижняя
клетка.
Откройте файл. Определите минимальную денежную сумму, которую может собрать Ладья.
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить) и пустую строку перед
самой первой (нажимаем правой кнопкой мыши на строку
и выбираем Вставить).

Выделяем всю таблицу и добавляем границы.
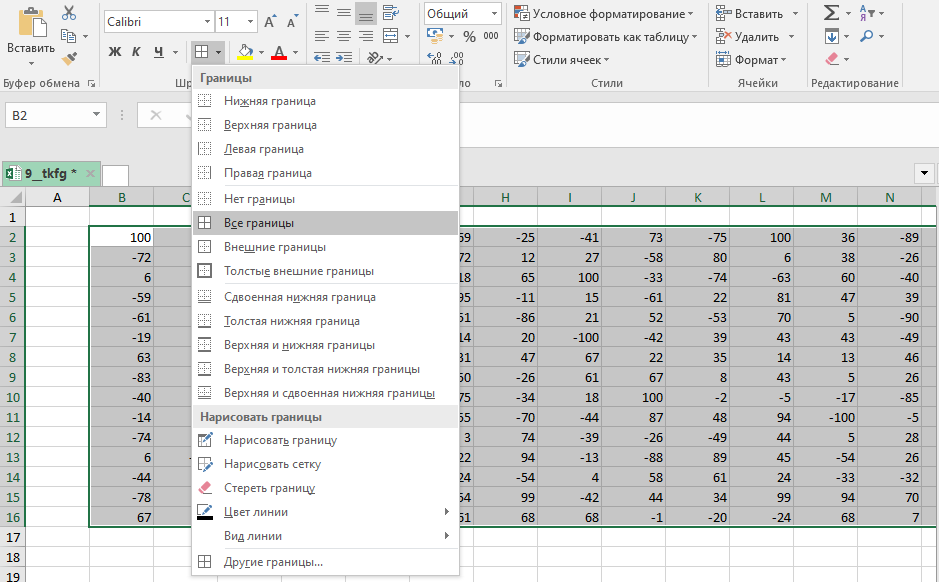
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
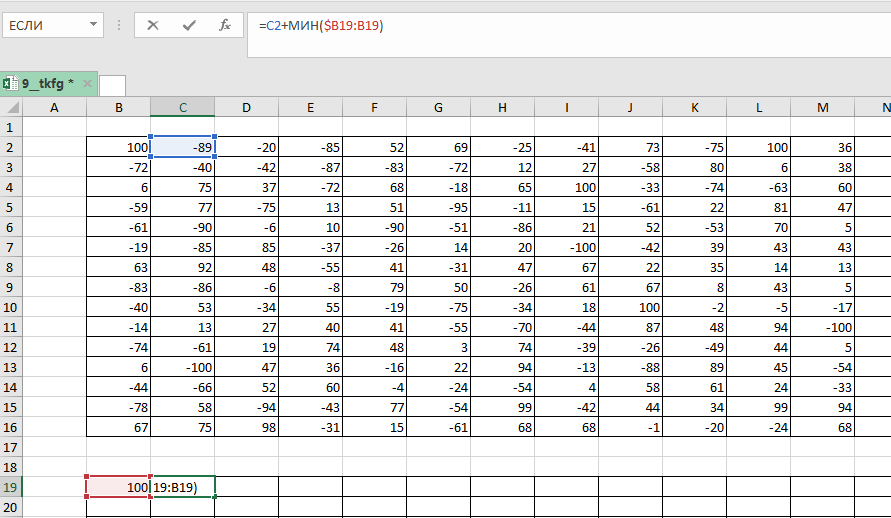
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =C2+МИН($B19:B19).
Копируем её на всю строку таблицы. В клетку записываем формулу =B3+МИН(B$19:B19).
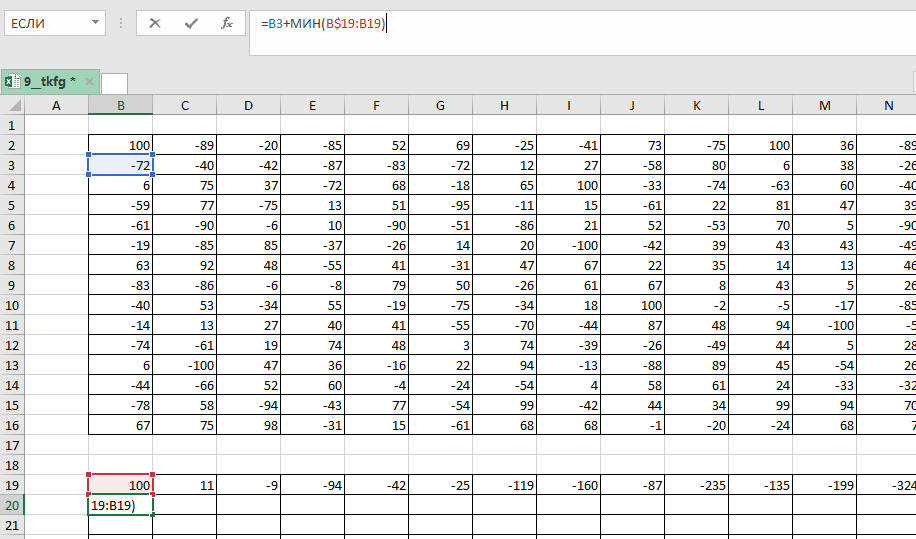
Копируем её на весь столбец таблицы. В клетку записываем формулу =C3+МИН(C$19:C19;$B20:B20).

Копируем её на все оставшиеся ячейки таблицы. Выписываем значение из правой нижней ячейки в ответ.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





