22.01 Стандартные задачи
Ошибка.
Попробуйте повторить позже
В файле содержится информация о совокупности вычислительных процессов, которые могут выполняться параллельно
или последовательно. Будем говорить, что процесс
зависит от процесса
, если для выполнения процесса
необходимы результаты выполнения процесса
. В этом случае процессы могут выполняться только
последовательно.
Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор
процесса , во втором столбце таблицы — время его выполнения в миллисекундах, в третьем столбце перечислены с
разделителем «
»
процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице
указано значение
.
Типовой пример организации данных в файле:
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
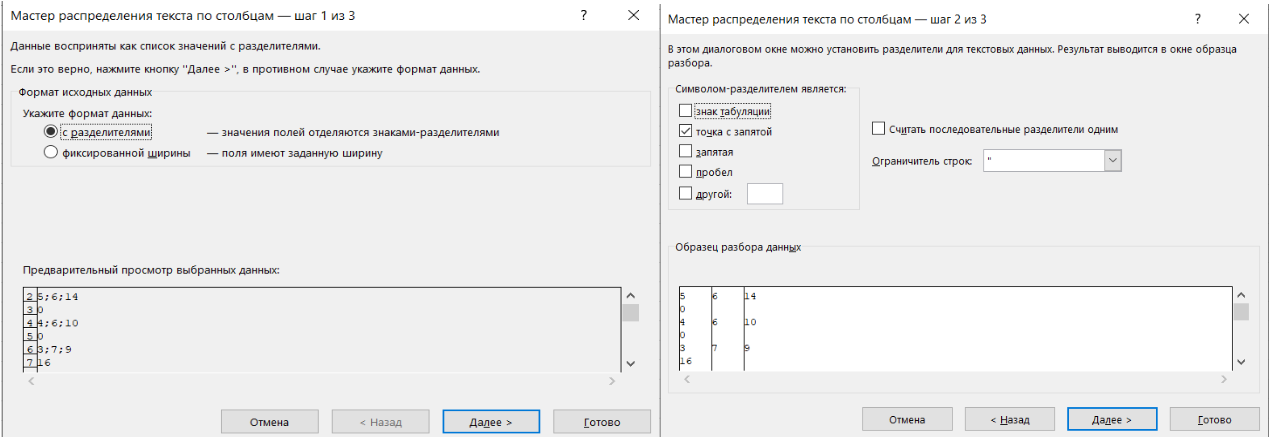
Открываем файл в редакторе таблиц. Выделяем столбец C и разбиваем данные, записанные в ячейках через точку с
запятой, по столбцам. Сделать это можно в разделе “Данные“ “Текст по столбцам“.

Выбираем “С разделителями“, затем ставим галочку у пункта “Точка с запятой“. Нажимаем “Готово“.
В ячейку вставляем формулу:
=ВПР(C2;$A:$O;15;0)
С помощью этой формулы мы будем брать из 15 столбца таблицы время окончания процесса . Не
забываем знак $ перед A и O для того, чтобы закрепить эти ячейки и чтобы при растягивании формулы
ничего не сломалось. Теперь растягиваем эту формулу до ячейки
, затем до ячейки
. Пока что
формулы работают некорректно из-за того, что у нас в таблице нет времени завершения 0 процесса.
Запишем в ячейки
и
нули, которые будут обозначать номер процесса и время его завершения,
соответственно.
После этого запишем в ячейку формулу:
=МАКС(I2:N2)+B2
Мы берем время окончания самого позднего процесса, от которого зависит процесс , после чего добавляем к этому
числу время выполнения процесса
. Теперь мы знаем минимальное время, через которое завершится процесс 1.
Растягиваем эту формулу до ячейки
.
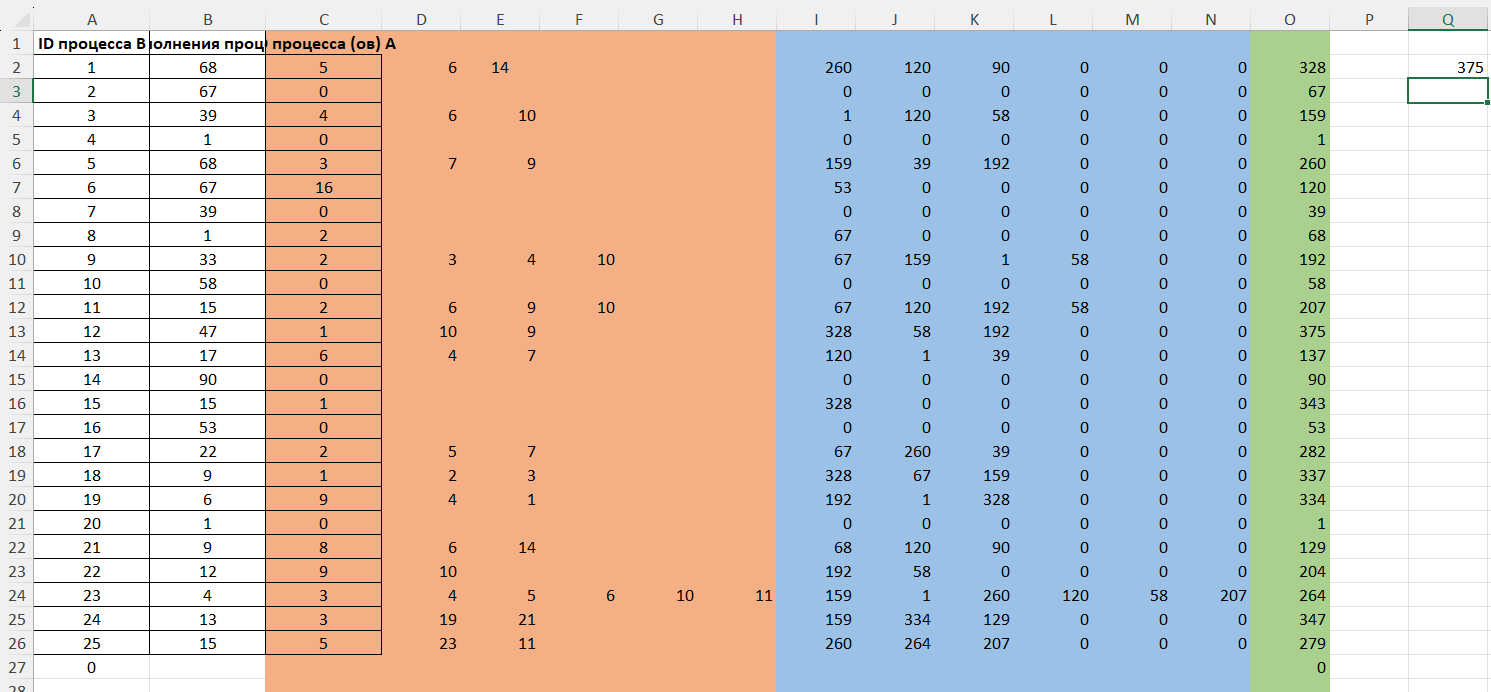
Прописываем справа от таблицы, в любой ячейке, формулу:
=МАКС(O:O)
и получаем минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





