Базовый вариант осеннего тура Турнира Городов
Ошибка.
Попробуйте повторить позже
Через вершину 
остроугольного треугольника 
проведены касательная 
к его описанной окружности, а также биссектрисы
и 
внутреннего и внешнего углов при вершине 
(точки 
и 
лежат на прямой 
). Докажите, что
Источники:
Заметим, что середина отрезка 
является центром окружности Аполлония точек 
и 
с коэффициентом 
Поэтому можно
предположить, что 
— центр окружности Аполлония и доказать, что 
— касательная к описанной окружности. Это равносильно
изначальной задаче, потому что касательная пересекает 
в одной точке.
Итак, 
поскольку биссектрисы смежных углов перпендикулярны. Нам нужно доказать равенство углов 
и 
тогда по обратной теореме об угле между хордой и касательной мы получим требуемое.
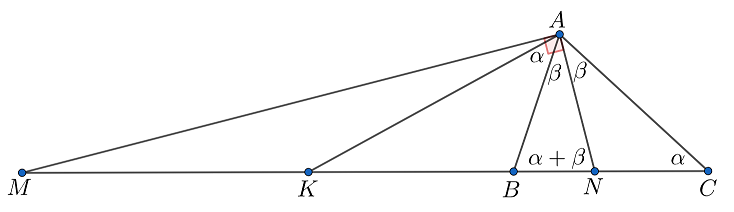
Обозначим угол 
через 
, а углы 
и 
— через 
. Отрезок 
— медиана, проведённая к гипотенузе, а значит
, то есть 
. Осталось заметить, что угол 
— внешний у треугольника 
. Таким образом,
. Получили требуемое.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
