Отбор Иннополиса
Ошибка.
Попробуйте повторить позже
Сколько корней имеет уравнение
Подсказка 1
Давайте попробуем искать решения для удобных нам m, например, для m > 0. Разбираться с отрицательными решениями не очень хочется, поэтому будем считать положительные (почему так можно?). Слева, должно быть, периодическая дробь, давайте найдём ее период, чтобы сделать рисунок ;)
Подсказка 2
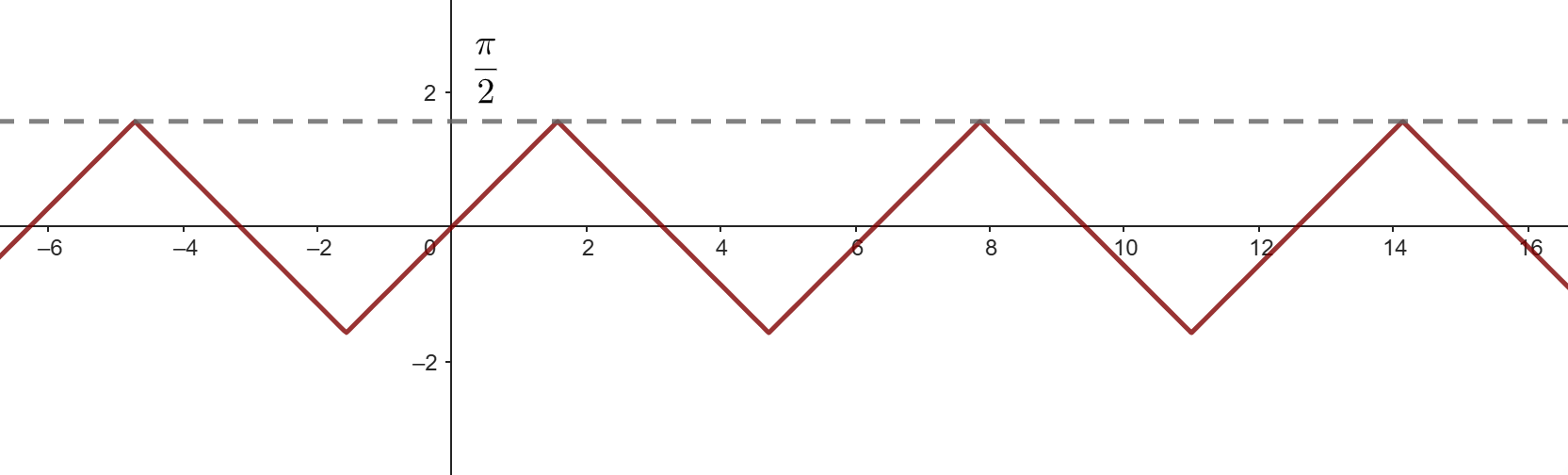
У функции слева период равен 2pi! Причём на промежутках такой длины она монотонна. Давайте сделаем рисунок!
Подсказка 3
Функция слева имеется "зубчатый" рисунок, а наибольшее значение по модулю равно pi/2. А какой график у функции справа? Подумаем, как они могут пересекаться?
Подсказка 4
Попробуйте посчитать количество промежутков монотонности, на которых прямая пересекает нашу "пилу". Но есть ли тут какой-то крайний случай?
Подсказка 5
Проверьте, когда же на крайнем для нас промежутке монотонности есть решение.
Подсказка 6
Это зависит от чётности количества промежутков, которые пересекает прямая!
Заметим, что количество положительных решений равно количеству отрицательных, ввиду нечётности функций в обеих частях уравнения,
а является решением, так как
Поэтому будет искать корни при
Так же из-за
нечётности функций количества решений при
и при
равны, поэтому будем искать число решений для положительного
На промежутке левая часть уравнения равна просто
по определению арксинуса. Пусть
где
Тогда
Получается, функция — это периодическая функция с периодом
и наибольшим значением
равным
достигаемым при
При этом на промежутках функция
монотонна и принимает все значения от
до
Функция — это возрастающая прямая, проходящая через точки
и
Получается, прямая может пересекать
только при
Более того, на промежутке
есть ровно одно решение уравнения — нулевое. Отсюда, все положительные
решения лежат в промежутке
Заметим, что на каждом промежутке монотонности может быть не более одного решения. Посчитаем, сколько промежутков
монотонности до
Пусть
Тогда — единственное целое число на промежутке
Тогда количество промежутков монотонности до
равно
Если — чётное, то
и на последнем промежутке монотонности
есть решение, а если
—
нечётное, то решения на этом промежутке нет.
Итак, количество положительных решений равно где
— остаток при делении
на 2. Тогда всего решений
Пример расположения графиков и
относительно друг друга при
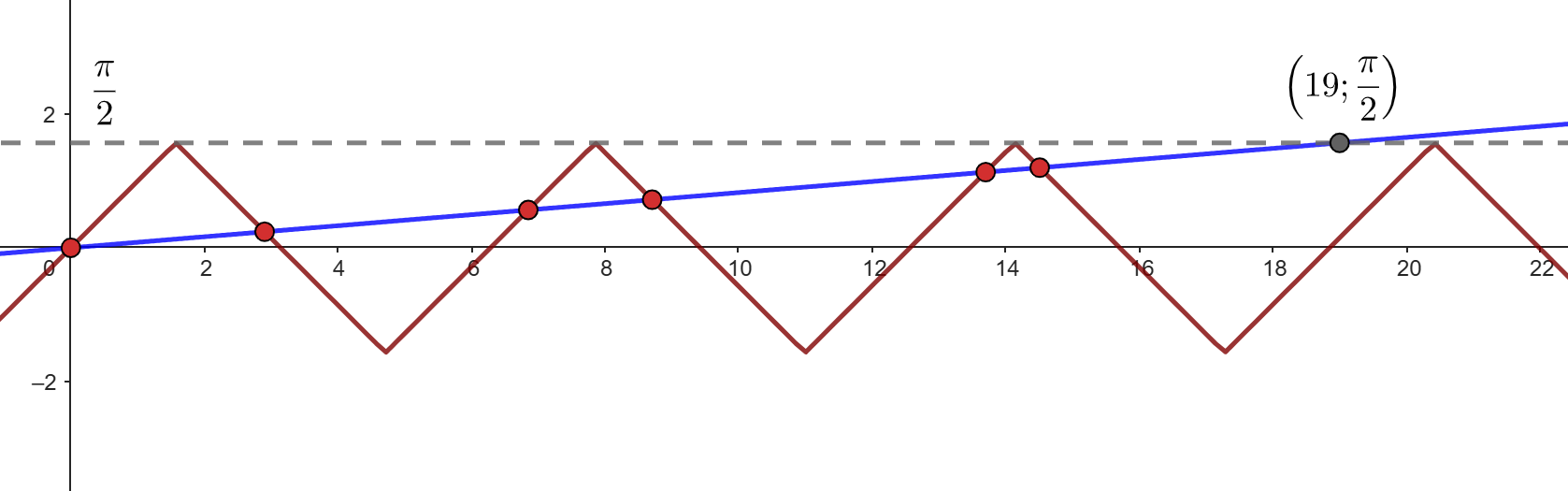
где
— единственное целое число на промежутке
— остаток при делении
на
2.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




