Тема ЮМШ (олимпиада Юношеской Математической Школы)

Отбор ЮМШ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела юмш (олимпиада юношеской математической школы)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#76650

Квадратный трёхчлен $x2− px+ q$ с натуральными коэффициентами имеет два корня. Оказалось, что если $q$ уменьшить на $30%$ , то разность его корней увеличится в 5 раз. Найдите такой трёхчлен с наименьшей возможной суммой корней.

Источники: ЮМШ-2023, 11 класс, отборочный тур (см. yumsh.ru) | ЮМШ-23/24, 11 класс, 1 отборочный тур (см. yumsh.ru)

Подсказки к задаче

Подсказка 1

Давайте вспомним, как мы находим корни в приведённом квадратном уравнении! А как можно выразить разность корней?

Подсказка 2

Да, корни находим через обычную формулу с дискриминантом. Тогда разность корней, это просто корень из дискриминанта нашего уравнения! Остаётся составить уравнение, в котором будет отражаться условие задачи!

Подсказка 3

Верно, из условия мы получаем, что 20p² = 81q. Остаётся найти минимальные p и q

Показать ответ и решение

По формуле корней квадратного уравнения имеем: $x = p±√p2−4q. 1,2 2$ Следовательно, $x − x = ∘p2-− 4q. 2 1$ После уменьшения $q$ на $30%$ разность корней станет равна $∘ 2---(7--) p − 4 10q.$ Следовательно, при условии, что $2 p − 4q ≥ 0,$ получаем

∘ ------ ∘ ------- 5 p2− 4q = p2− 14q ⇐⇒ p2 = 81q > 4q ⇐ ⇒ 4⋅5⋅p2 = 34 ⋅q. 5 20

По теореме Виета сумма корней квадратного трёхчлена $x2− px+ q$ равна $p.$ Наименьшее натуральное $p,$ удовлетворяющее равенству $4⋅5⋅p2 = 34⋅q,$ это $32 =9,$ так как $p2$ должно делиться на $34.$ Тогда $q = 20.$

Ответ:

$x2− 9x+ 20$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76651

Найдите количество функций $f :{1,2,3,4,5,6} → {1,2,3,4,5,6}$ для которых верно $f(f(f(x)))=x$ для всех $x∈ {1,2,3,4,5,6}$ .

Источники: ЮМШ-2023, 11 класс, отборочный тур (см. yumsh.ru) | ЮМШ-23/24, 11 класс, 1 отборочный тур (см. yumsh.ru)

Показать ответ и решение

Возьмем какое-нибудь число $a ∈{1,2,3,4,5,6}.$ Тогда возможны два варианта:

1. Если $f(a)= a,$ то и $f(f(f(a)))= a.$

2. Предположим $f(a)= b и b⁄= a.$ Тогда $f(b)= c, где c⁄= a,c⁄= b.$ Иначе
(а) Если $f(b)= a, то f(f(f(a)))= f(f(b)) =f(a)=b ⁄=a.$
(b) Если $f(b)= b, то f(f(f(a)))= f(f(b))= f(b) =b⁄= a.$
И так как $a =f(f(f(a)))= f(f(b))= f(c),$ то $f(c)=a.$

Таким образом, для любого $a∈ {1,2,3,4,5,6}$ либо $f(a)=a,$ либо есть три различных числа таких, что $f(a)= b,f(b) =c и f(c)= a.$

При этом любая функция с таким свойством подходит. Тогда найдем число функций с необходимым свойством.

1. Нет ни одной тройки элементов, что $f(a)= b,f(b)= c, и f(c)= a.$ Значит, для всех чисел $a∈{1,2,3,4,5,6}$ верно $f(a)= a.$ Такая функция одна.

2. Есть одна тройка элементов, что $f(a)= b,f(b)= c, и f(c)=a.$ Выбрать тройку можно $C36$ способами. При этом есть два способа задать функцию в тройке. Итого $2C36$ функций.

3. Есть две тройки элементов, что $f(a)= b,f(b)= c, и f(c)= a.$ Выбрать первую тройку можно $C36$ способами, остальные три элемента образуют вторую тройку. Но варианты, в которых выбрали в первую тройку $a,b,c$ и выбрали все кроме $a,b,c$ одинаковые. То есть $C36 :2$ способов разбить элементы на две тройки. При этом в каждой тройке есть два способа задать функцию. Итого $2⋅2⋅C36 :2 =2C36$ функций.

Всего число функций равно

1 +2C36 + 2C36 = 81

Ответ: 81

Ошибка.
Попробуйте повторить позже

Задача 3#76652

Окружности $ω 1$ и $ω 2$ пересекаются в точках $A$ и $B$ . Прямая $l 1$ , проходящая через точку $A$ , второй раз пересекла окружность $ω 1$ в точке $C$ , а $ω2$ — в точке $D$ . Прямая $l2$ , проходящая через точку $B$ , второй раз пересекла окружность $ω1$ в точке $E$ , а $ω2$ — в точке $F.$ Оказалось, что прямая $CE$ касается $ω2$ в точке $G$ (точка $E$ лежит на отрезке $CG$ ). Докажите, что $BG$ — биссектриса $∠DBE$ .

Источники: по мотивам отборочного тура ЮМШ 23/24

Подсказки к задаче

Подсказка 1

Посчитаем уголочки! Как использовать вписанность? Выразим угол FBE и подумаем, как считать углы дальше.

Подсказка 2

Угол между касательной равен вписанному углу, опирающему на хорду. Найдите угол DFC и свяжите его с DAF :) Чему равен угол FBE?

Показать доказательство

Поскольку четырехугольники $ABEC$ и $ADGB$ вписанные, то

∠BEG = ∠CAB = ∠BGD

Также, поскольку прямая $CE$ касется окружности $ω2$ , по теореме об угле между касательной и хордой

∠BDG = ∠BGE

Теперь рассмотрим треуугольники $△BEG$ и $△BGD.$ В них имеются две пары равных углов $(∠BEG = ∠BGD, ∠BGE = ∠BDG ),$ значит, третьи углы у них тоже равны, т.е.

∠DBG = ∠GBE

Получаем, что $BG$ — биссектриса угла $∠DBE.$

$PIC$

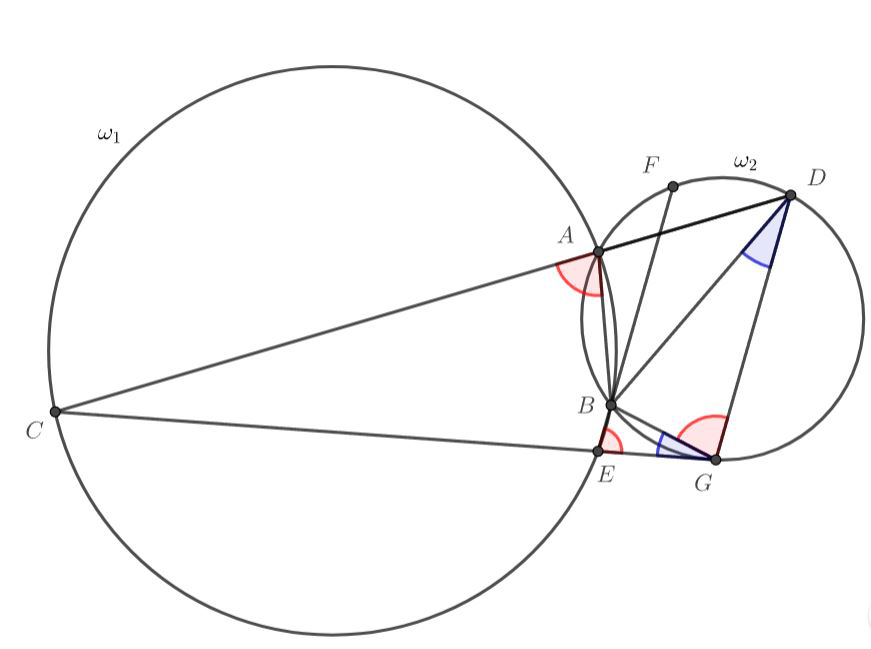
Замечание. Если точка $G$ лежит внутри отрезка $CE,$ то чертёж меняется, но решение остаётся аналогичным. Попробуйте решить задачу и для этого расположения точек.

Ошибка.
Попробуйте повторить позже

Задача 4#76654

Докажите, что для любого $x∈ [0;2]$ верно

x ∘ ------- 2 +1− 10,5x +4 ≤0.

Источники: ЮМШ-23/24, 11 класс, 1 отборочный тур (см. yumsh.ru)

Подсказки к задаче

Подсказка 1

Немного преобразуем неравенство так, чтобы нам приходилось сравнивать показательную функцию с функцией с корнем. Как они выглядит на графике? Что у них общего и чем они различаются?

Подсказка 2

Одна из них — выпуклая, другая — вогнутая. Ка кто можно использовать, сравнивая значения в некоторых точках? Какие точки стоит рассмотреть, чтобы применить эти свойства?

Подсказка 3

Рассмотрите точки, в которых графики пересекаются.

Показать доказательство

Решение 1.

Перепишем неравенство, данное в условии:

x ∘------- 2 ≤ 10,5x+ 4− 1.

Посмотрим на график степенной функции. Если соединить две точки, принадлежащие графику, отрезок их соединяющий лежит выше графика.

С графиком функции $y =√10,5x-$ наоборот: если соединить две точки, принадлежащие графику, отрезок их соединяющий лежит ниже графика. График функции $√------- 10,5x+ 4− 1$ это сдвинутый по осям абсцисс и ординат график функции $√---- y = 10,5x.$ Значит, и для графика функции $√ ------- 10,5x+ 4− 1$ верно: если соединить две точки, принадлежащие графику, отрезок их соединяющий лежит ниже графика.

Подставим значения $x =0, и x= 2$ в левую и правую части неравенства. Получаем, что графики функций $x √------- 2 и 10,5x+ 4− 1$ проходят через точки $(0;1) и (2;4).$ Тогда все значения функции $x 2$ лежат ниже отрезка, соединяющего точки $(0;1) и (2;4),$ а все значения $√------- 10,5x+ 4− 1$ выше.

То есть в каждой точке отрезка $[0;2]$ все значения функции $x 2$ не меньше чем значения $√ ------- 10,5x +4− 1.$

∘------- 2x ≤ 10,5x +4− 1

x ∘ ------- 2 +1− 10,5x +4 ≤0.

______________________________________________________________________________________________________________________________________________________

Решение 2.

Обозначим

------- f(x)= 2x +1− ∘ 10,5x+4.

Докажем, что $f(x)≤ 0$ на всём отрезке $[0;2].$

Производная $f(x)$ на отрезке $[0;2]$

f′(x)= ln(2)⋅2x− -√-10,5--- 2 10,5x+ 4

Приравняем $f′(x)$ к $0$ :

ln(2)⋅2x− -√-21----= 0 4 10,5x+ 4

x 21 ln(2)⋅2 = 4√10,5x-+4

x∘------- --21- 2 10,5x+ 4= 4ln(2)

Функции $√ ------- 2x и 10,5x+ 4$ – возрастающие на отрезке $[0;2].$ Тогда $√------- 2x 10,5x+ 4$ тоже возрастающая. Значит, производная имеет не более одного корня на отрезке $[0;2].$ То есть $f(x)$ имеет не более одной точки экстремума на отрезке $[0;2].$

На концах $f(0)= f(2)= 0.$

Тогда если на отрезке $[0;2]$ нет точек экстремума и монотонность не меняется, то $f(x)=0$ на всем отрезке. Если точка экстремума лежит на отрезке $[0;2],$ то возможны два варианта:

1. Это точка минимума. Тогда функция убывает от 0 до точки минимума, а затем возрастает до 2.

2. Это точка максимума. Тогда функция возрастает от 0 до точки максимума, а затем убывает до 2.

Отметим, что $f(1)<0,$ то есть

f(1)= 21+ 1− ∘10,5⋅1+-4= 3− ∘14,5 <0

Значит, возможен только первый вариант. Тогда $f(x)≤ 0$ на всём отрезке $[0;2].$

Ошибка.
Попробуйте повторить позже

Задача 5#76655

Сумма всех натуральных делителей числа $n$ более чем в 100 превосходит само число $n$ . Докажите, что есть сто идущих подряд чисел, каждое из которых имеет общий делитель с $n$ больший 1.

Источники: ЮМШ-2023, 11 класс, отборочный тур (см. yumsh.ru) | ЮМШ-23/24, 11 класс, 1 отборочный тур (см. yumsh.ru)

Показать доказательство

Сначала докажем лемму.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма.

Пусть $φ (n)$ - функция Эйлера числа $n.$ (Количество чисел от $1$ до $n$ взаимно простых с $n.$ ) Тогда для любого натурального числа $n >1$ справедливо неравенство

∑ n2 d < φ(n)- d|n

_________________________________________________________________________________________________________________________________________________________________________________

Доказательство леммы.

Запишем сумму делителей числа через произведение сумм степеней его простых делителей. Если $n =pα1pα2...pαk, 1 2 k$ то

∑ 2 α1 2 α2 2 αk d =(1+ p1+p1+ ...+ p1 )(1+ p2+ p2+ ...+ p2 )...(1+ pk +pk+ ...+ pk ) d|n

Используя формулу суммы геометрической прогрессии, получаем:

∑ d= (1+ p + p2 +...+ pα1)(1+ p +p2+ ...+ pα2)...(1+ p +p2+ ...+ pαk)= d|n 1 1 1 2 2 2 k k k

(pα11+1 − 1)(pα22+1− 1)...(pαk+1− 1) = ----(p1−-1)(p2-− 1)...(pkk− 1)--.

Функция Эйлера вычисляется по формуле $φ(n)=pα11−1(p1− 1)pα22−1(p2− 1)...pαkk− 1(pk− 1).$ Тогда чтобы получить $φ(n)$ в знаменателе, домножим числитель и знаменатель на $pα11−1pα22−1...pαkk−1$

(pα11+1−-1)(pα22+1−-1)...(pαkk+1−-1)= (p1− 1)(p2− 1)...(pk− 1)

α1−1 α2−1 αk−1 α1−1 α2−1 αk−1 = p1--p2α1−.1..pk--(pα12−1-− 1)(p2-α−k−11)...(pk---−-1)= p1 (p1− 1)p2 (p2− 1)...pk (pk− 1)

(p2α1 − pα1−1)(p2α2− pα2−1)...(p2αk− pαk−1) p2α1p2α2...p2αk n2 = --1----1-----2--φ(2n)------k----k----< -1--2φ(n)--k--= φ(n)

_________________________________________________________________________________________________________________________________________________________________________________

Решение задачи.

По условию и лемме

∑ -n2- 100n < d|nd< φ(n).

Тогда

100n< -n2-⇒ φ(n)< n-. φ(n) 100

То есть количество чисел от $1$ до $n$ взаимно простых с $n$ меньше $-n- 100.$

Рассмотрим два случая: $n$ делится на $100$ и $n$ не делится на $100.$

1. Число $n$ делится на $100.$ Тогда можно разбить числа от $1$ до $n$ на $n-- 100$ групп по $100$ идущих подряд чисел. Если количество чисел от $1$ до $n$ взаимно простых с $n$ меньше $n-- 100$ , то хотя бы в одной группе не будет числа взаимно простого с $n$

2. Число $n$ не делится на $100.$ Тогда среди чисел $2$ до $n$ можно выделить $-n- [100]$ групп по $100$ идущих подряд чисел. Если в каждой группе будет число взаимно простое с $n$ , то чисел взаимно простых с $n$ хотя бы $n [100]+ 1$ ( $1$ тоже взаимно проста с $n$ ). Это противоречит тому, что количество чисел от $1$ до $n$ взаимно простых с $n$ меньше $n 100-$