1.17 Окружность: описанная около многоугольника
Ошибка.
Попробуйте повторить позже
Треугольники и
имеют общее основание,
— точка пересечения
и
Найдите
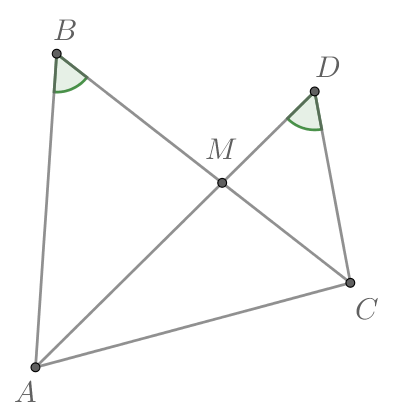
Так как то около четырёхугольника
можно описать окружность. Покажем это:
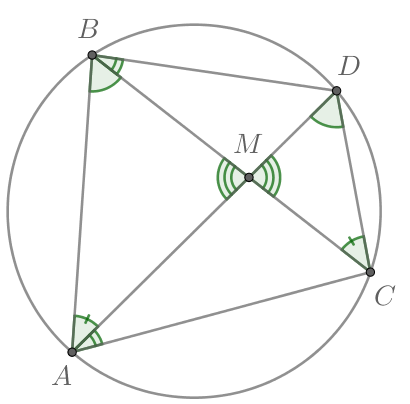
и
— вертикальные, тогда
тогда треугольники
и
подобны
по двум углам, откуда получаем:
Но углы и
также вертикальные, тогда
и треугольники
и
подобны, так как если
угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол в одном треугольнике,
пропорциональны соответствующим сторонам другого, то такие треугольники подобны.
Из подобия получаем:
тогда
так как это сумма углов треугольника .
Если в выпуклом четырёхугольнике сумма противоположных углов равна то около него можно описать окружность, тогда
около
можно описать окружность.
Так как произведение отрезков одной из пересекающихся хорд равно произведению отрезков другой, то
то есть
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




