Комбинаторика на устном туре Турнира Городов

Первое решение.

Рассмотрим клетчатый квадрат размером и удалим из него внутренний центральный квадрат оставив только рамку толщиной 1. В рамке будет как раз 40 клеток. Докажем, что на плоскости нет клетчатого прямоугольника, содержащего ровно 20 из этих 40 клеток.

Допустим, такой прямоугольник есть. Пусть в нём есть клетки из обеих вертикальных сторон рамки. Тогда каждая горизонтальная сторона рамки либо полностью включена в прямоугольник, либо вовсе не включена. Если включена ровно одна горизонтальная сторона, число клеток в прямоугольнике нечётно, если обе — клеток 40 (слишком много), а если ни одной — клеток максимум (слишком мало).

Значит, в прямоугольнике могут быть клетки лишь из одной вертикальной стороны рамки, и, аналогично, лишь из одной горизонтальной стороны рамки. Но эти стороны соседние, и суммарно в них максимум 19 клеток — слишком мало. Противоречие.

Второе решение.

Рассмотрим клетчатый прямоугольник и удалим из него клетки и Останется ровно 40 клеток. Предположим, что нашёлся клетчатый прямоугольник, в котором ровно 20 отмеченных клеток. Он может затрагивать одну, две или три горизонтали с номерами

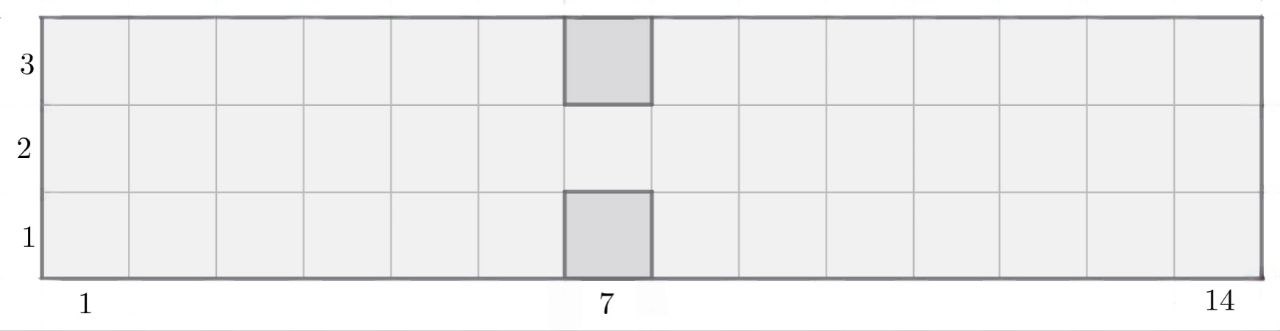
Если он затрагивает одну горизонталь, то в нём не более 14 отмеченных клеток.

Если он задевает 2 горизонтали (одна из них — вторая), то он задевает вертикаль с номером 7 (иначе в нём не более 14 клеток). Тогда эта вертикаль вносит в прямоугольник нечётное число отмеченных клеток, а остальные — чётное. Поэтому общее число отмеченных клеток в прямоугольнике нечётно.

Если он задевает все три горизонтали, то число отмеченных клеток в нём либо кратно 3 (если он не задевает 7-й вертикали), либо имеет остаток 1 при делении на 3 (иначе).

В каждом из случаев получаем противоречие.

Замечание. Возможны другие решения. Например, подходит квадрат с вырезанным центральным квадратом но доказательство более длинное.