Теория чисел на Верченко
Ошибка.
Попробуйте повторить позже
Вася хочет заполнить квадратную таблицу (криптографическую мозаику) размера целыми числами от 1 до 16 по
следующему правилу. Сначала он выбирает четыре целых числа
. Затем первую строку Вася заполняет
числами
вторую строку — числами
третью
и, аналогично, четвертую
При этом числа Вася выбрать должен так, чтобы все числа в таблице оказались различными. Сумеет ли Вася это сделать?
Если да, то чему равны
?
Источники:
Подсказка 1
Видите вопрос "сможет ли...?" и сразу руки чешутся как-нибудь доказать, что не получится? :) Давайте сначала успокоимся и попробуем посмотреть на то, что от нас просят. В табличке должны получиться различные остатки по модулю 17, причем эти aᵢ очень подозрительно выглядят... 1 и 16 в сумме дают 17, 3 и 14 тоже.... Что можно сказать?
Подсказка 2
Да, в одном столбце получаются числа bᵢ + 1, bᵢ + 4, bᵢ - 4, bᵢ - 1 (mod 17). Полученная симметрия так и бросается в глаза, правда? Вот бы можно было выбрать какое-нибудь b и наглядно видеть остатки от чисел, которые оно образует... Вам же наверняка тоже не хочется долго перебирать и считать аᵢ
Подсказка 3
А что если остатки по модулю 17 изобразить по кругу? И правда, если мы выберем какое-нибудь число b из круга, то число b+r пойдет по кругу на r шагов от него в сторону увеличения, а b-r, на те же r шагов в сторону уменьшения. Получается, если выбрать какое-нибудь число b, то оно вычеркивает два числа рядом с собой и два числа на расстоянии 4. Получится ли у нас подобрать еще 3 числа так, чтобы вычеркнутые числа не пересекались?
Подсказка 4
Да, получится. Если это вызывает затруднения, заметьте, что само число b в табличку не входит, поэтому оно может быть среди вычеркнутых. Если вы пойдете по кругу от самого первого выбранного вами числа и выберете числа на расстоянии 1, 7 и 11, то у вас точно никакие вычеркнутые числа не пересекутся :)
Заметим, что
Представим остатки полученных от
в виде круга остатков. Числа получаются от
смещением на
или
шага по часовой
или против часовой стрелки в зависимости от знака.
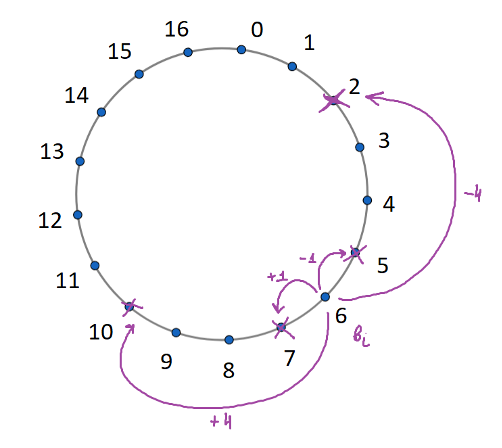
Заметим, что важен лишь набор , а не их порядок, тогда без ограничения общности выберем пару
,
— одно из чисел
или такое число, которого нет в таблицы. Докажем, что
тогда обязательно соседняя с
.
Предположим противное, то есть что ни одна пара ,
не являются соседями (так как иначе можем взять их в качестве
,
).
случай (
): возьмём
(если все различные числа сдвинуть на одинаковое число по модулю
, то они
останутся одинаковыми, а значит мы можем взять
), в таблицу уже попали числа:
, тогда “запрещённые” позиции —
(они получены путём прибавления и вычитания
,
по модулю
к полученным клеткам в таблице), а значит,
—
, но тогда они соседи — противоречие.
случай (
): переименуем
,
в
,
и получится случай 1.
![]()
случай (
аналогично, без ограничения общности, не входит в таблицу): Все остальные числа входят, так как с каждой
в таблицу
добавляются по 4 числа. Рассмотрим число
, у нас уже "запрещены"числа
для
, иначе
входит в таблицу и
,
иначе в таблице есть повторяющиеся числа, тогда
,
получается, что
, т.е.
.
Посмотрим на “запрещённые” числа для :
, но
снова соседние.
Мы получили, что обязательно должны быть 2 соседних числа. С одной стороны, зачёркнутые ячейки на расстоянии от
и
образуют место для
и
(поскольку есть две свободные ячейки вокруг двух зачеркнутых чисел). С другой стороны, при выборе двух
, набор двух оставшихся определяется однозначно, поэтому итого вариантов выбора комбинации столько же, сколько и выбор двух подряд
идущих чисел в круге, т.е.
.
![]()
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




