Комбинаторика на Верченко
Ошибка.
Попробуйте повторить позже
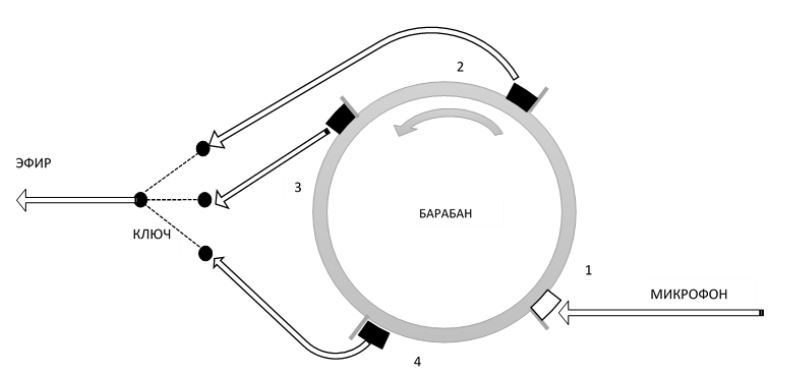
Звук записывается на магнитный слой барабана, который вращается с постоянной скоростью, совершая один оборот за секунды. Рядом с
барабаном по окружности через равные расстояния размещены записывающая
и три читающие головки
В каждый
момент времени в телефонную линию передается сигнал с одной из читающих головок. Устройство спроектировано так, что каждый
участок сигнала будет передан в линию один раз, а сама передача стартует, как только начало записи окажется у
-й
читающей головки. Сколько различных вариантов звука, переданного в линию, может получиться, если сообщение длилось
секунд?
Источники:
Подсказка 1
Пусть передача длилась n секунд. Как можно представить звук, переданный на линию?
Подсказка 2
Переключение между читающими головками происходит раз в секунду, поэтому можно разбить весь звук на n фрагментов и рассматривать их перестановки.
Подсказка 3
Обозначим количество перестановок за T(n). Передача закончится на (n+1)-ой секунде. Какие фрагменты могут быть переданы в этот момент на линию?
Подсказка 4
Мог быть передан n-ый или (n+1)-ый фрагмент. Рассмотрите оба случая.
Подсказка 5
Пусть был передан (n+1)-ый фрагмент. Значит, он не мог быть передан на предыдущей секунде. Чему тогда равно количество перестановок фрагментов?
Подсказка 6
T(n-1). Проведите аналогичные рассуждения для n-ого фрагмента и выведите формулу для T(n).
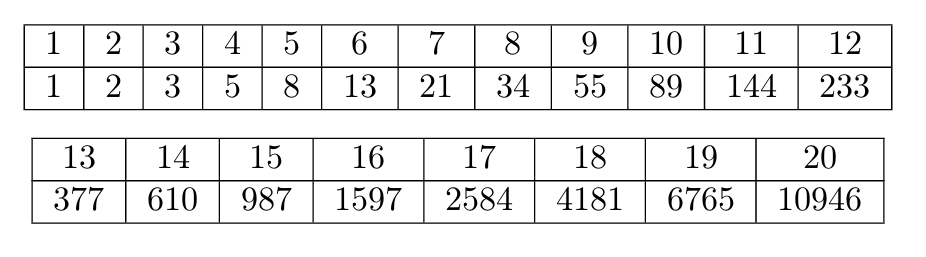
Пусть передача длилась секунд. Так как переключение между читающими головками происходит раз в секунду, весь звук можно
разбить на
фрагментов по 1 секунде, тогда звук, переданный на линию, будет будет перестановкой этих фрагментов. Обозначим
количество возможных перестановок за
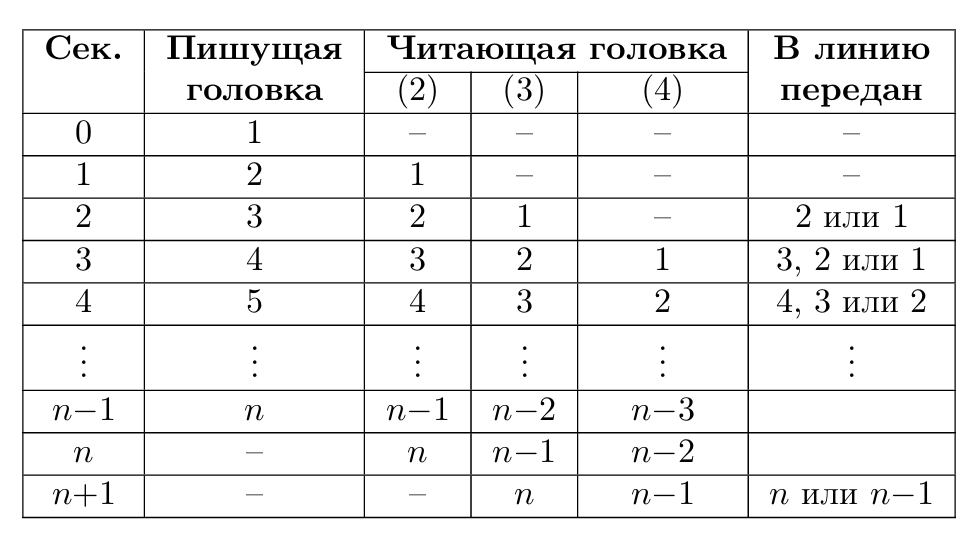
Представим весь процесс в виде таблицы, элементами которой являются номера фрагментов. Например, на второй секунде, с которой
начинается передача, на пишущей головке будет третий фрагмент звука, второй фрагмент звука будет на второй читающей головке, а
первый фрагмент — на третьей. Передача закончится на ой секунде. В этот момент на линию может быть передан
ый или
ый фрагмент звука. Рассмотрим оба случая:
- 1.
-
Пусть в момент времени
бы передан
ый фрагмент. Тогда он не мог быть передан на предыдущей секунде. Если посмотреть на таблицу, становится ясно, что количество перестановок фрагментов в этом случае совпадает с
иначе говоря, количеством способов переставить звук длины
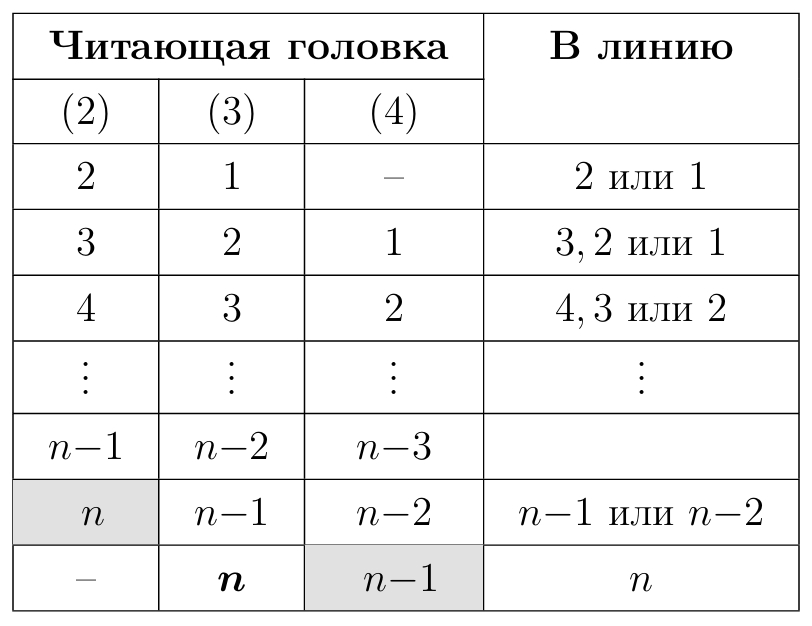
- 2.
-
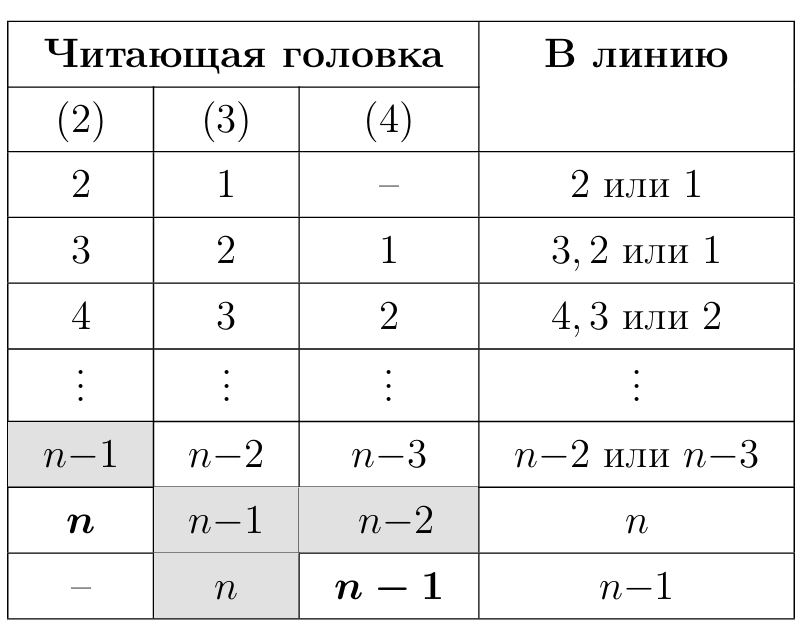
Пусть в момент времени
бы передан
ый фрагмент. Тогда он не мог быть передан на предыдущих секундах. Так как
ый фрагмент должен уйти на линию, он должен быть передан в момент
Тогда до
ой секунды должно быть передано
последовательных фрагмента, что соотвествует
способам.
Таким образом, Для любого
чтобы найти
достаточно найти
и
Останется только с
использованием формулы
вычислить нужное значение.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




