Комбинаторика на БИБНе
Ошибка.
Попробуйте повторить позже
На координатной плоскости дан прямоугольник с целочисленными координатами вершин, отличный от квадрата. Докажите, что можно провести несколько прямых, параллельных сторонам прямоугольника, так, что прямоугольник разобьется на квадраты с целочисленными координатами вершин.
Источники:
Подсказка 1
Давайте сначала "причешем" задачу, чтобы нам было удобнее её решать. Нам дали произвольный прямоугольник с вершинами в целых точках. Тогда как, не умаляя общности, можно его представить на координатной плоскости?
Подсказка 2
Верно, можно изобразить прямоугольник с одной из вершин в начале координат O, потому что иначе сделаем сдвиг на соответствующий вектор, и ничего не поменяется. Давайте теперь решать задачу на языке векторов. Введите обозначения для координат вершин прямоугольника. Как теперь можно записать условие перпендикулярности смежных сторон с точкой O?
Подсказка 3
Ага, на языке векторов это будет значить, что их скалярное произведение равно 0. Отлично, уже что-то! Теперь нужно как-то воспользоваться целостностью координат. Попробуем разобрать два случая, когда координаты точек взаимно просты и когда это не так. Давайте сначала рассмотрим первый случай. Почему в этом случае можно сказать, что наш исходный прямоугольник это квадрат?
Подсказка 4
Пусть координаты вершин были (p;q) и (m;n). Тогда из прошлой подсказки мы знаем, что pm + qn = 0, а из взаимной простоты получаем, что p = ±n, q = ±m. В этом случае всё понятно. Пусть теперь НОД(p;q) = k. Тогда какие координаты точек на одной стороне хорошо бы рассмотреть? Аналогично с другими координатами.
Подсказка 5
Верно, давайте рассмотрим координаты точек (pi;qi), где i = 1, 2, 3,..., k-1, и проведём через них прямые, параллельные стороне OB. Они пересекут в каких-то точках противоположную сторону прямоугольника, причём для них выполняется определённое равенство для векторов. Теперь если же m и n взаимно просты, то проделайте те же действия. Осталось только понять, почему это решает задачу и аккуратно довести её до конца.
Пусть — данный прямоугольник. Без ограничения общности можно считать, что
— начало координат: иначе сместим начало
координат в точку
а в конце сделаем сдвиг на целочисленный вектор
Обозначим векторы
где
,
— целые числа. Поскольку
и
взаимно перпендикулярны, их скалярное произведение равно нулю, т.е.
(этот факт также следует из соотношения для угловых коэффициентов перпендикулярных прямых
и
).
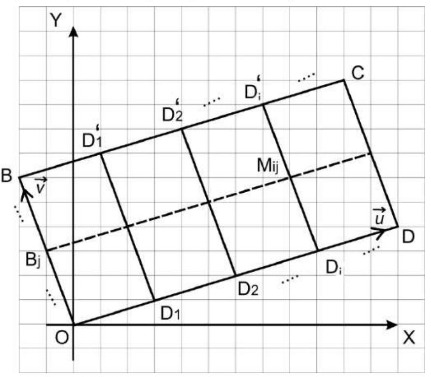
Рассмотрим сначала случай, когда и
не взаимно просты. Тогда
НОД(
В этом случае рассмотрим
на стороне
промежуточные точки
где
Проведём через точки
прямые,
параллельные стороне
Они пересекут сторону
в точках
где
Таким образом, точки и
имеют целочисленные координаты и тем самым, прямые
разбивают прямоугольник
на
прямоугольников с целочисленными вершинами. Назовем это разбиением первого
типа.
Аналогично, если и
не взаимно просты, то прямыми, параллельными стороне
разобьем
на меньшие
прямоугольники с целочисленными вершинами. Назовем это разбиением второго типа; прямые этого разбиения проходят через
промежуточные точки
на стороне
где
а
— наибольший общий делитель
и
Заметим, что в случае, когда одновременно
и
прямые первого и второго разбиений разбивают
прямоугольник
на
равных прямоугольников с вершинами в точках
где
т.е. все вершины имеют целочисленные координаты.
Итак, приходим к случаю, когда координаты каждого из векторов взаимно просты. Но тогда из равенства
получим, что
(действительно, из этого равенства следует, что
делится на
и, в то же время,
делится на
значит,
аналогично,
с учетом знака в данном равенстве). В этом случае стороны прямоугольника
равны:
и наш прямоугольник квадрат.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




