Планиметрия на Питергоре
Ошибка.
Попробуйте повторить позже
Точка — центр вневписанной окружности треугольника
касающейся стороны
в точке
а точка
диаметрально
противоположна точке
на описанной окружности этого треугольника. На отрезках
выбраны точки
соответственно таким образом, что
где r — радиус вписанной окружности треугольника
Докажите, что точки
лежат на одной окружности.
Подсказка 1
У нас в условии есть центры вписанной и вневписанной окружностей - попробуем посчитать какие-то углы, найти равные…хочется еще равные отрезки как-то использовать, не так ли? Еще заметим, что точки Z, T у нас практически одинаковы по построению, поэтому будет досрочно сделать выводы для одной из них, а потом произнести волшебное «аналогично». Не понятно, как подобраться к углам требуемого «вписанного» четырехугольника, поэтому попробуем доказать, что серединные перпендикуляры к его стороны пересекаются в одной точке.
Подсказка 2
С помощью подсказки 1, учитывая, что угол АВА´ прямой, приходим к тому, что ZBIaY равнобедренная трапеция! Что мы тогда может сказать о серединной перпендикуляре к ZY? А к BIa? Серединный перпендикуляр к последнему отрезку несложно найти с помощью известной леммы, которая ищет такую точку W, что WB = WIa. Аналогичные действия проделывает и с точкой T)
Подсказка 3
Серединные перпендикуляры к ZY и YT проходят через середину дуги BC окружности (ABC) по лемме о Трезубце и в силу того, что эти серединные перпендикуляры совпадают с серединными перпендикулярами к BIa и CIa. Осталось лишь доказать, что серединный перпендикуляр к XY проходит через эту же точку.
Подсказка 4
Для этого отложим на продолжении отрезка XIa за Х такую точку I’, что XI’ = r и подумаем о треугольнике IaI’I.
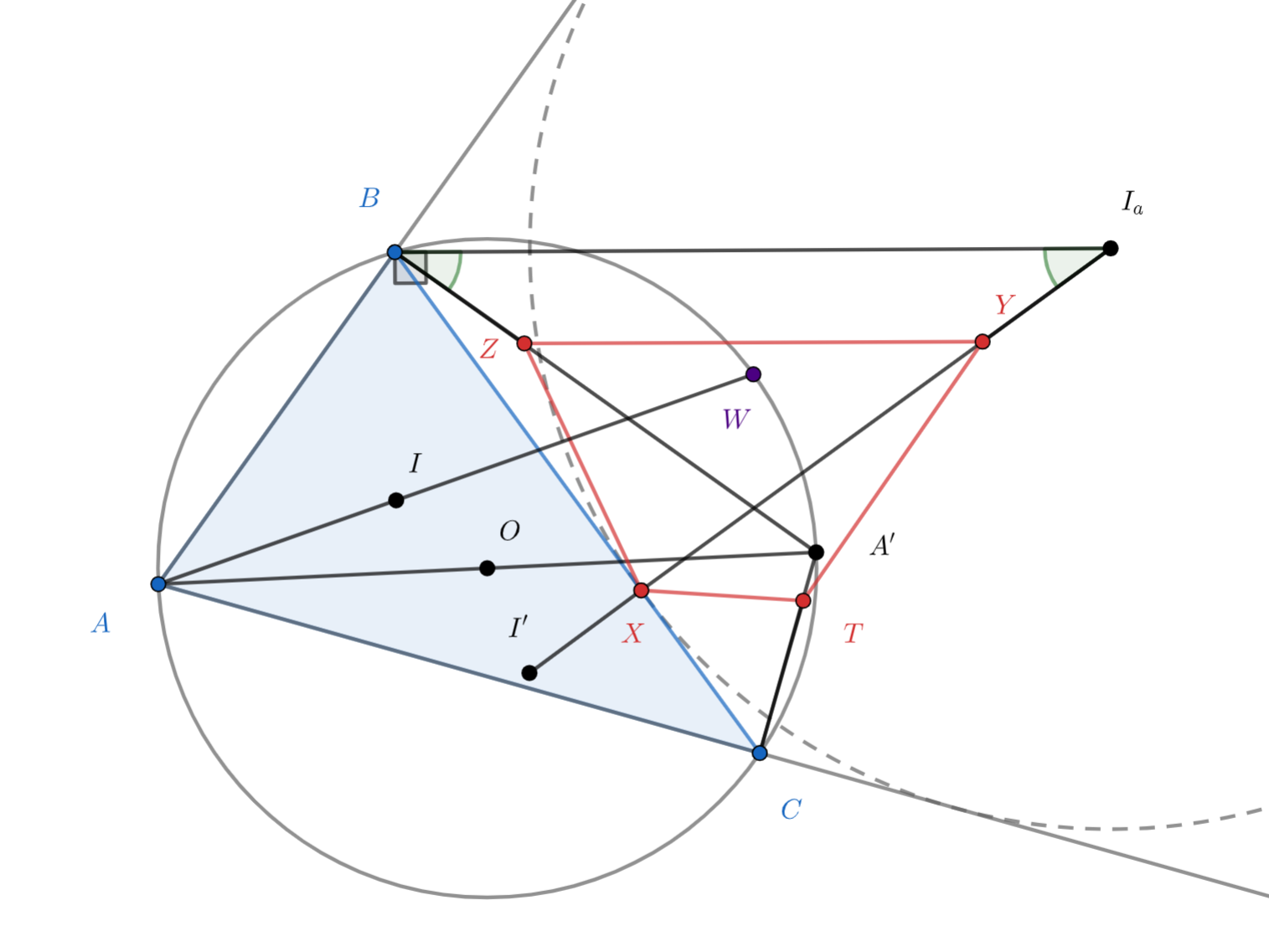
Из условия сразу следует, что . Кроме этого, если
— центр вписанной окружности, то
. Из этих равенств сразу
следует, что
. Поскольку прямая
— внешняя биссектриса угла
, угол
, и
поэтому
Таким образом, и
. Это значит, что четырехугольник
— равнобедренная трапеция. Поэтому
серединный перпендикуляр к отрезку
совпадает с серединным перпендикуляром к отрезку
. Последний по лемме о трезубце
проходит через середину
дуги
описанной окружности треугольника. Аналогично, через
проходит и серединный перпендикуляр
к отрезку
Осталось понять, почему через проходит серединный перпендикуляр к отрезку
. Отметим на продолжении
отрезка
за точку
такую точку
, для которой
. Иными словами,
— прямоугольный треугольник с
прямым углом при вершине
. По уже упоминавшейся лемме о трезубце, точка
— середина его гипотенузы
.
Следовательно, она лежит на серединном перпендикуляре
совпадающем с серединным перпендикуляром к отрезку
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




