Стереометрия на ИТМО

Обозначим тетраэдр центр сферы, вписанной в каркас — а саму сферу — Объём тетраэдра равен сумме объёмов маленьких тетраэдров и

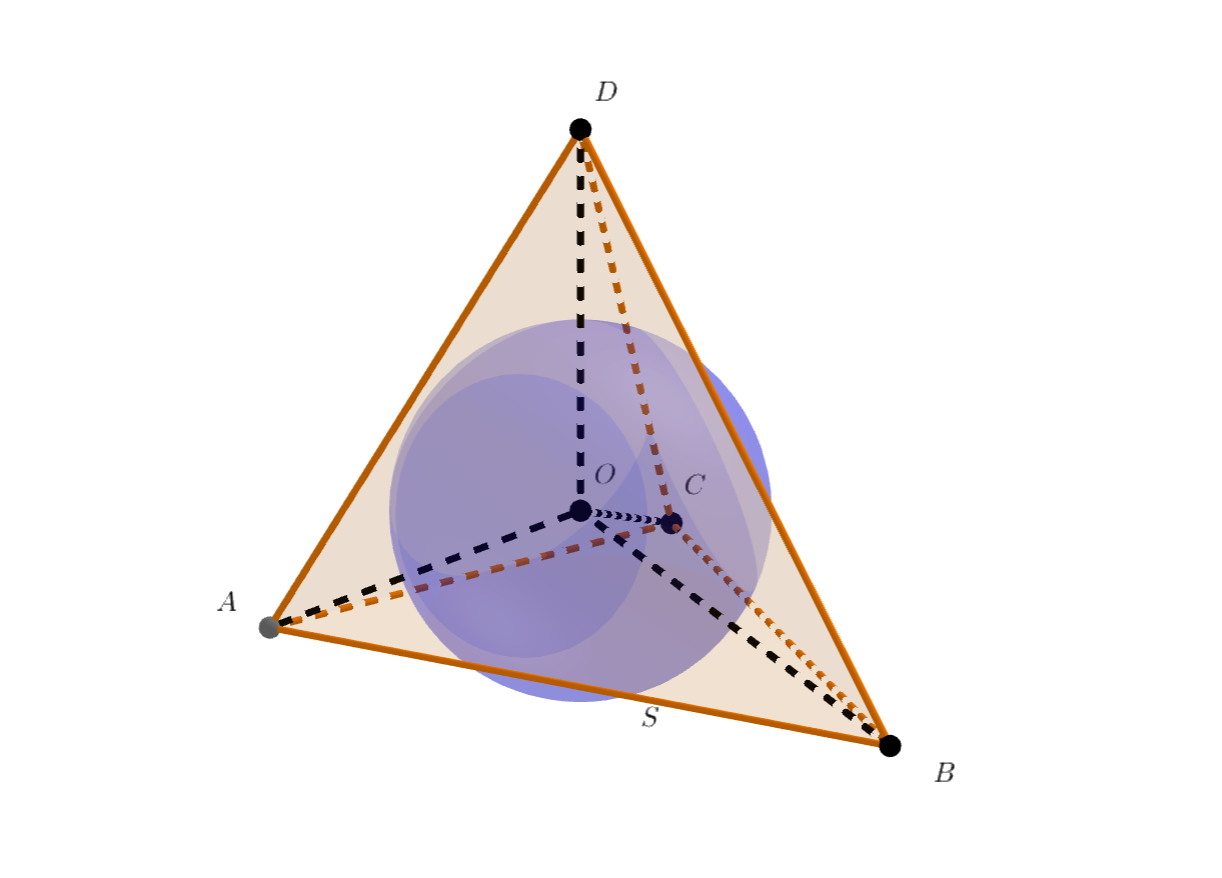
Пересечение и плоскости это вписанная окружность треугольника Обозначим за её центр, тогда — высота тетраэдра Пусть — радиус сферы — радиус вписанной окружности треугольника Тогда выполняется равенство Тогда

где — полупериметр треугольника По неравенству о среднем геометрическом и среднем квадратичном получаем

то есть

Таким образом,

Складывая объёмы четырёх маленьких тетраэдров, получаем

а сумма полупериметров граней это в точности сумма длин рёбер тетраэдра. Значит,