Стереометрия на ИТМО

Пусть наши кубы — это и с общей гранью . Пусть также треугольное сечение первого куба — это , где точка лежит на , точка на , а точка — на . Одна из сторон четырёхугольного сечения второго куба — отрезок . Две другие — продолжения отрезков и на грани второго куба, назовём эти отрезки и . Чтобы сечение было четырёхугольным, точки и должны находиться на одной грани второго куба, а это может быть только грань .

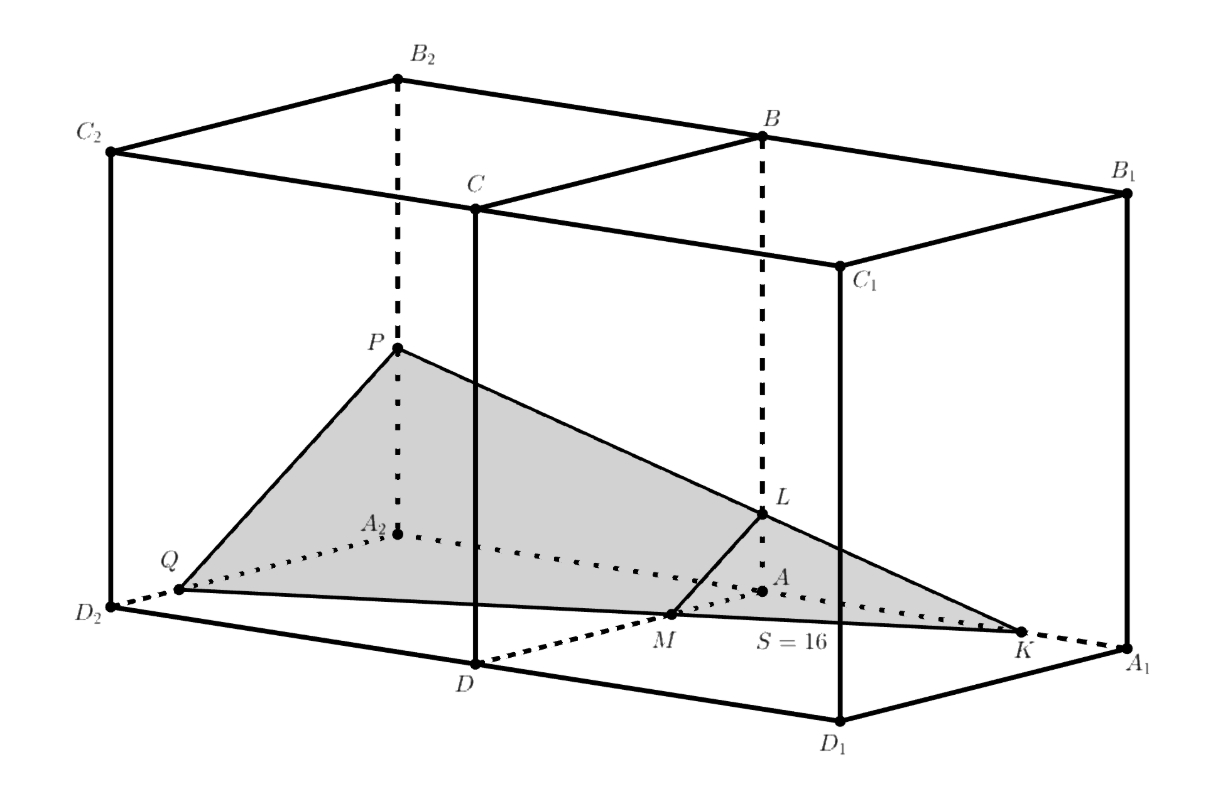
Значит, четырёхугольное сечение второго куба — это трапеция . Нахождение её наибольшей площади равносильно нахождение наибольшей площади треугольника , который подобен треугольнику . Обозначим этот коэффициент подобия . Тогда . То есть наша задача равносильна задаче о нахождении максимального коэффициента подобия.

С другой стороны, по теореме Фалеса . То есть коэффициент подобия тем больше, чем меньше , а значит, наша задача — минимизировать , или, что то же самое, минимизировать .

Пусть у нас есть треугольник, вершины которого расположены на трёх рёбрах куба, выходящих из одной точки, на расстояниях и . Найдём формулу площади этого треугольника. Это можно делать по-разному, например, через векторное произведение, или посчитав двумя способами площадь тетраэдра, образованного вершинами треугольника и вершиной куба, но мы вычислим эту площадь по формуле Герона, зная стороны треугольника: и .

Посмотрим на эту формулу для треугольника и отрезков . С одной стороны, нам надо минимизировать , а с другой - максимизировать площадь. Очевидно, для этого и должны быть максимальны, то есть равны ребру .

Как мы знаем, , то есть , откуда

Подставляя эти значения в формулу, получаем:

Соответственно,

откуда

Правая часть этого равенства убывает при , а значит, данное уравнение на имеет не больше одного решения. Конкретное решение в большинстве вариантов легко подбирается из этого равенства, так как оно целочисленное.

При мы получаем уравнение

откуда сразу возникает желание проверить , что оказывается верным.

Ответ получается как разность площадей двух треугольников и равен