Планиметрия на Иннополисе
Ошибка.
Попробуйте повторить позже
Окружность — это, как известно, множество точек на плоскости, удаленных от заданной точки (центра) на фиксированное расстояние
(радиус окружности), а число — это отношение длинны окружности к длине ее диаметра. В этом определении по умолчанию
предполагают, что речь идет об Евклидовом расстоянии/длине, которая вычисляется на двумерной координатной плоскости
для
отрезка с концами в точках
и
по формуле
Однако, Евклидово определение
длины — не единственно-возможное. Например, манхэттенская длина отрезка с концами в точках
и
вычисляется по формуле
(Название «манхэттенское расстояние» связано с уличной планировкой
Манхэттена, представляющую собой прямоугольную сетку улиц: «На север с юга идут авеню, на запад с востока — стриты» В. В.
Маяковский, «Бродвей».) Чему равно отношение манхэттенской длинны Евклидовой окружности к манхэттенской длине ее
диаметра?
Источники:
Подсказка 1
Для начала было бы сподручно вообще понять, что из себя представляет махэттенская длина Евклидовой окружности. Да, из условия задачи знаем определение манхэттенской длины, но надо понять, как с её помощью посчитать длину окружности. Может, есть какая-то закономерность между манхэттенской длиной цепочки точек и длиной лишь между первой и последней из этих точек?
Подсказка 2
Не забудьте доказать, что связь, полученная вами, верна для всех случаев. Попробуйте рассмотреть дугу Евклидовой окружности в 90°. А что будет если соединить все точки этой дуги непрерывной ломаной? Как посчитать её манхэттенскую длину?
Подсказка 3
Осталось только обобщить полученный вами результат на всю окружность, и дальше дело элементарной арифметики :)
Рассмотрим произвольную ломаную (см. рисунок) такую, что абсциссы ее узлов ведут себя монотонно (на рисунке они не убывают) и ординаты ее узлов тоже ведут себя (возможно, по-другому, но тоже) монотонно (на рисунке они тоже не убывают). Тогда манхэттенская длина такой ломаной (то есть сумма манхэттенских длин ее отрезков) равна манхэттенскому расстоянию между ее концами.
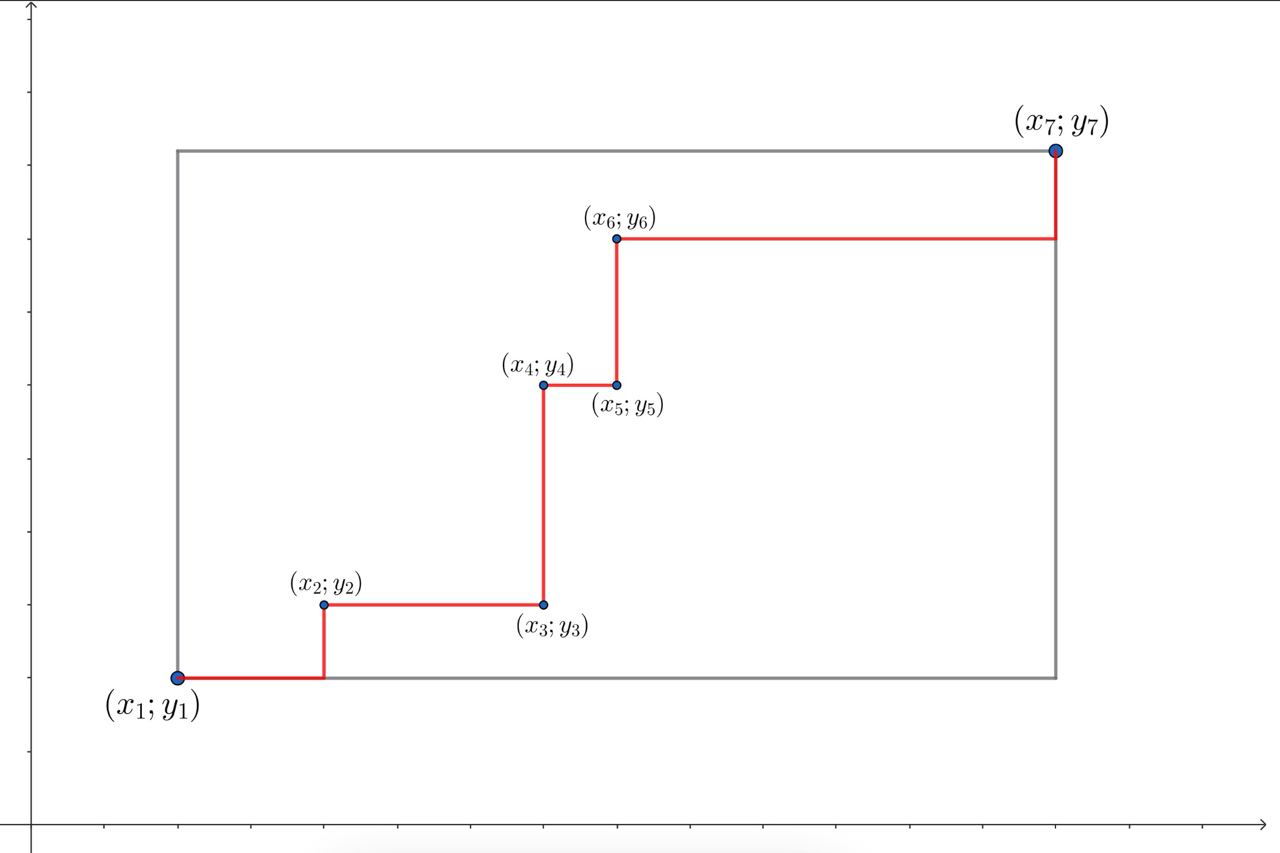
Доказательство этого утверждения должно рассматривать разные варианты (абсциссы и ординаты не убывают, абсциссы не убывают, а ординаты не возрастают, и так далее), но мы ограничимся только случаем, представленном на рисунке:
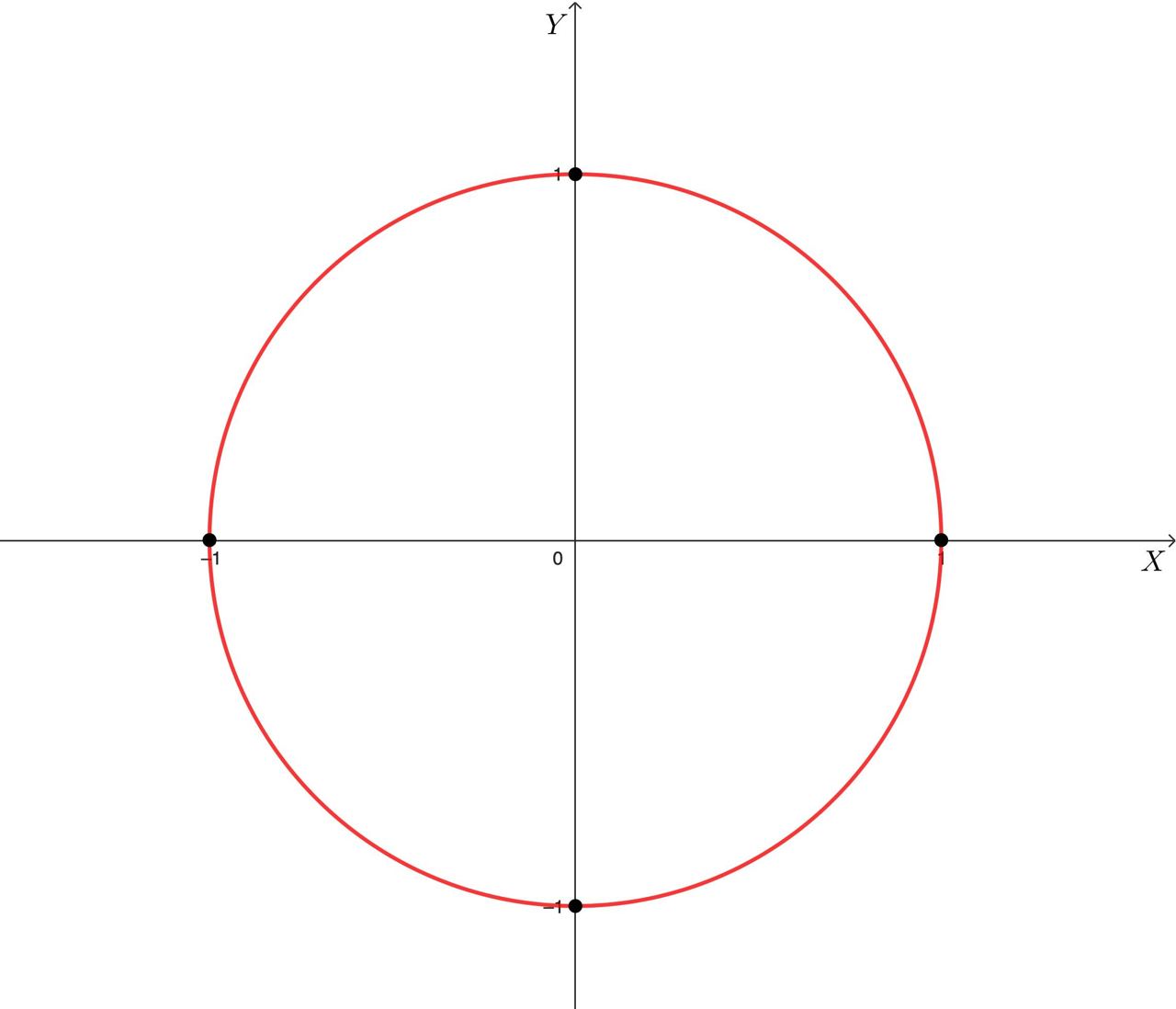
Следовательно, манхэттенская длина каждого из четырех сегментов
и
евклидовой окружности манхэттенского радиуса 1 с центром в начале координат равны
манхэттенская длина всей этой Евклидовой окружности равна а отношение манхэттенской длины Евклидовой окружности к
манхэттенской длине ее диаметра равно
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




