Планиметрия на Иннополисе
Ошибка.
Попробуйте повторить позже
Дан треугольник . Существует единственный набор таких трёх окружностей
и
, которые лежат внутри треугольника,
попарно друг друга касаются, а также каждая из них касается сторон соответствующего угла:
касается сторон
и
касается сторон
и
касается сторон
и
.
Обозначим точку касания окружностей и
как
. Аналогично определяются точки
и
.
Дизайнер хочет сконструировать люстру-витраж из цветного стекла, в которой стороны треугольника - это прочный
(пренебрежимо) лёгкий контур, в который вписан массивный плоский диск весом 1 кг, а также добавлены уравновешивающие веса в
вершинах
и
треугольника так, чтобы точка подвеса люстры находилась на пересечении отрезков
и
(остальные детали люстры имеют пренебрежимо малый вес). Докажите, что такой проект люстры осуществим и определите
уравновешивающие веса в вершинах (то есть такие, чтобы люстра висела горизонтально, закреплённая только в точке подвеса), если
радиусы окружностей
- это
, а радиус вписанного диска треугольника равен
.
Источники:
Подсказка 1
Попробуйте доказать, что m_A = 0.5(r−r_A)/r_A, m_B = 0.5(r−r_B )/r_B, m_C = 0.5(r−r_C )/r_C подходят.
Подсказка 2
Во-первых, обозначим за I центр вписанной окружности. Давайте разберёмся в каком отношении делят О_A, O_A , O_C отрезки AI, BI, CI соответственно.
Подсказка 3:
Заметим, что гомотетия в точке A с коэффициентом r/r_A переводит ω_A в ω, где ω - вписанная окружность. Значит, AI/AO_A = r/r_A. Значит, AO_A/O_AI = r_A/(r−r_A) . Аналогично,
BO_B/O_BI = r_B/(r−r_B) и CO_C/O_CI = r_C/(r−r_C) . Подумайте теперь, как предъявленные веса связаны с этими отношениями.
Подсказка 4
Будем обозначать точку X с весом w как (X, w). Тогда (I, 1) равносильна системе (I, 0.5) и (I, 0.5). А теперь заметим, что m_A/0.5 = (r-r_A)/(r_A). Вспомним правило группировки масс. Есть две точки (X₁, w₁), (X₂, w₂). Тогда их центр масс (Y, w#) таков, что Вектор →(YX₁) × w₁ + →(YX₂) × w₂ = 0, а w# = w₁ + w₂. Тогда для пары точек (A, (r-r_A)/r_A) и (I, 0.5) центром масс будет (O_A, m_A + 0.5), так как →(O_AA) × m_A + →(O_AI) × 0.5 = r_A/r × →(IA) × 0.5(r-r_A)/r_A + (r - r_A)/r × →(AI) × 0.5 = 0. Аналогично для O_B и O_C. Подумайте, что делать дальше?
Подсказка 5
Тогда cистема точек (I, 1), (A, m_A), (B, m_B), (C, m_C) эквивалентна системе (I, 0.5), (I, 0.5), (A, m_А), (B, m_B), (C, m_C), которая, в свою очередь, эквивалентна системе (O_A, m_A + 0.5), (O_B, m_B + 0.5), (C, m_C) = (O_A,r/2r_A), (O_B, r/2r_B), (C, m_C). Как дальше можно сгруппировать массы, зная, что T_(AB) лежит на O_AO_B и делит в хорошем отношении этот отрезок?
Подсказка 6
Заметим, что T_(AB)O_A = r_A, T_(AB)O_В = r_B, а значит →(T_(AB)O_A)/→(T_(AB)O_B) = -r_A/r_B, а значит →(T_(AB)O_A) × r./2r_A + →(T_(AB)O_B) × r/2r_B →(T_(AB)O_A) × r/2r_A - →(T_(AB)O_A) × r_B/r_A × r/2r_B = 0. Значит T_(AB) — центр масс (O_A, r/2r_A) и (O_B, r/2r_B). Итого, cистема (O_A, r/2r_A), (O_B, r/2r_B), (C, m_C) эквивалентна (T_(AB), r/2r_A + r/2r_B), (C, m_C). Что теперь можно сказать про общий центр масс исходной системы, учитывая, что мы свели её к системе всего из ДВУХ точек?
Подсказка 7
Центр масс системы из двух точек всегда лежит на прямой, которую образуют эти точки. Тогда центр масс системы (T_(AB), r/2r_A + r/2r_B), (C, m_C) лежит на прямой CT_(AB). Но стоп, мы же нигде не пользовались тем, что точка C — какая-то особенная, в сравнении с A и B, ведь условие симметрично относительно этой тройки точек. Как можно изящно завершить решение задачи, используя это понимание?
Подсказка 8:
Точно! Если центр масс системы (T_(AB), r/2r_A + r/2r_B), (C, m_C), то есть центр масс исходной системы, лежит на прямой CT_(AB), то в силу симметричности условия, он также лежит на AT_(BC) и на BT_(AC), ведь мы можем просто сдвинуть названия точек по циклу и применить те же рассуждения. Остаётся самый лёгкий шаг. Что следует из того, что точка лежит на трёх прямых?
Обозначим массы в вершинах и
соответственно как
и
. Докажем, что массы
подходят.
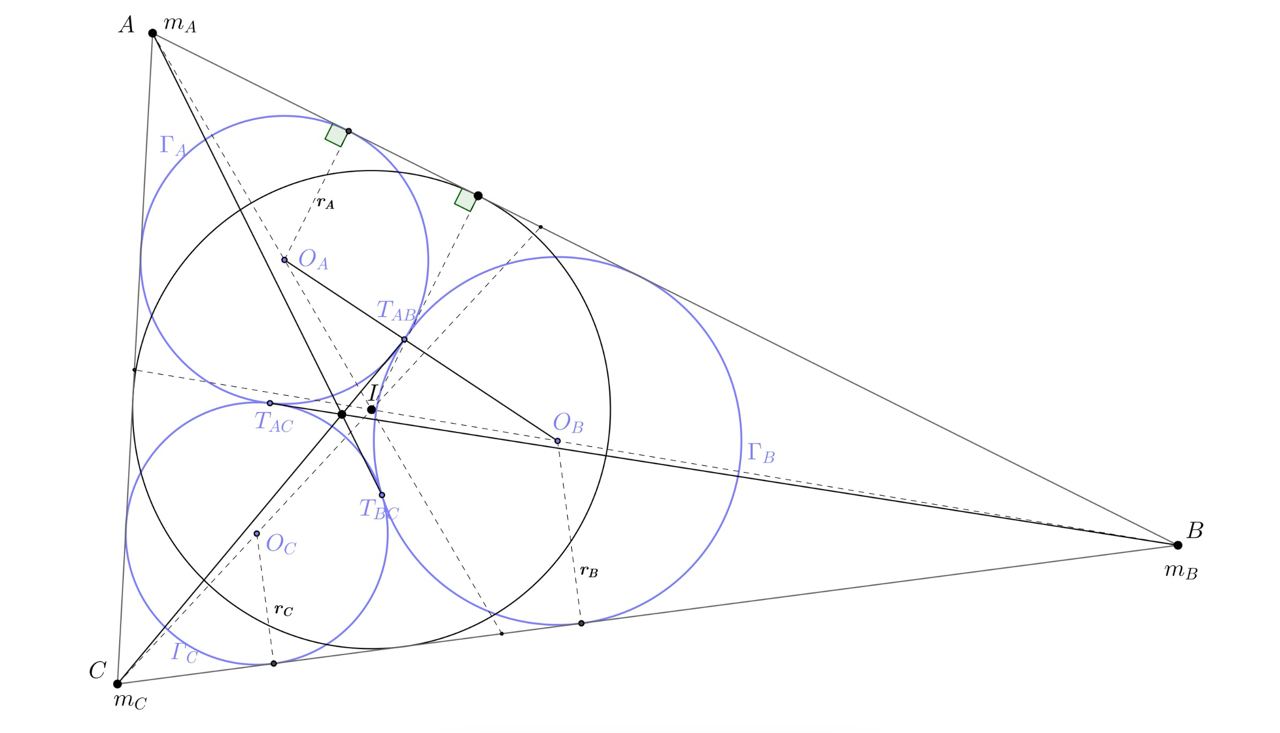
Покажем, что центр масс системы нагруженных точек кг) находится в точке
— центре окружности
(см. рисунок). Из подобия соответствующих прямоугольных треугольников вытекает, что
. Тогда
. Чтобы точка
была центром масс указанных точек, по правилу рычага, должно выполняться
. Подставив указанное значение для
, легко видеть, что правило рычага выполняется и для пары точек
(и центра масс
), и для пар точек
и
с центрами масс
и
соответственно.
Тогда, пользуясь принципом перегруппировки масс, имеем, что центр масс системы точек и
совпадает с центром масс системы точек
, что совпадает с центром масс системы
.
Но . Аналогично,
и
. Значит, указанная система нагруженных точек
переписывается в виде
.
Окружности и
, по выбору, касаются. Значит, отрезок
равен по длине
и делится точкой
на
части длины
и
. Но тогда для точек
и точки
выполняется равенство
.
Значит,
— центр масс системы из этих двух точек, а значит, центр масс изначальной системы
и
,
после перегруппировок, совпадает с центром масс системы двух точек:
. Как следствие, этот центр масс
лежит на отрезке
. По абсолютно аналогичным причинам, центр масс изначальной четвёрки нагруженных точек
лежит также на отрезках
и
. Таким образом, выбранные веса
удовлетворяют требованию
задачи.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




